22. Координатний метод і його застосування для розв’язування задач

Сутність координатного методу, як і векторного, полягає в тому, що геометрична задача перекладається на мову алгебри, і її розв’язання зводиться до розв’язання рівнянь, нерівностей чи їх систем.

З курсу стереометрії відомо, що рівняння площини, що проходить через точку перпендикулярно ненульовому вектору в прямокутній системі координат має вигляд: , або , де

Положення площини в просторі однозначно визначається заданням трьох точок, що не лежать на одній прямій. Нехай дана площина перетинає осі координат в точках , , , але не проходить через початок координат. Підставивши координати цих точок у загальне рівняння площини, отримаємо: , , , де числа відмінні від нуля. Звідси знаходимо: і рівняння приводиться до вигляду:

Отримане рівняння називають рівнянням площини у відрізках. Його часто застосовують при розв’язуванні задач.

Як відомо, відстань між двома точками і обчислюється за формулою:

Користуючись даною формулою можна легко вивести рівняння сфери.

Нехай пряма l проходить через дану точку і паралельна ненульовому вектору Вектор називають напрямним вектором прямої l.

Довільна точка належить прямій l тоді і тільки тоді, коли вектори або де t– деяке число (параметр). Дане співвідношення в координатах рівносильне системі рівнянь:

Дану систему називають параметричними рівняннями прямої.

Якщо пряма l паралельна осі то вектор є напрямним вектором, і рівняння прямої прийме вигляд: .

Нехай жодна з координат вектора не рівна 0. Тоді виключивши з отриманих рівнянь параметр t, отримаємо рівняння:

Отримані рівняння називаються канонічними рівняннями прямої.

Виведемо формулу для обчислення відстані від даної точки до площини , заданої в прямокутній системі координат рівнянням Нехай перпендикуляр, проведений з точки до площини , перетинає її в точці . Тоді Так як вектор перпендикулярний площині і колінеарний вектору то згідно з визначенням скалярного добутку, Позначимо Тоді

Виразимо скалярний добуток, що стоїть в знаменнику дробу, через координати векторів і Отримаємо:

Точка лежить в площині , тому . Таким чином, маємо:

Враховуючи, що , отримаємо:

Наведемо основні векторні співвідношення і формули, які використовуються для розв'язування стереометричних задач.

1. Для будь-яких трьох точок Α, Β,C має місце рівність:

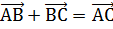
2. Для будь-яких трьох точок Α, Β і О виконується рівність:

3. Для того, щоб точка С лежала на прямій АВ, необхідно і достатньо, щоб існувало таке число k, що

4. Нехай А і В – дві різні точки прямої і точка С – точка даної прямої така, що .

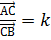5. Чотирикутник ABCD є паралелограмом тоді і тільки тоді, коли виконується одна з наступних рівностей:

, , , де O – довільна точка простру.

6. Якщо вектори і неколінеарні, то для будь-якого вектора , що лежить в одній площині з і , існує єдина пара чисел x і y таких, що .

7. В просторі для кожного вектора існує єдиний розклад за трьома некомпланарними векторами , , : .

8. Нехай точки А, В, С не лежать на одній прямій; тоді для того щоб точка D лежала в площині АВС, необхідно і достатньо, щоб існувала така пара чисел α і β, що .