36) Производная неявной функции

о многих задачах функция  y(x) задана невным образом. Например, для приведенных ниже функций невозможно получить зависимость y(x) в явном виде. Алгоритм вычисления производной  y'(x) от неявной функции выглядит следующим образом: Сначала необходимо продифференцировать обе части уравнения по отношению к x, предполагая, что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции;Решить полученное уравнение относительно производной  y'(x).Рассмотрим для иллюстрации несколько примеров.    Пример 1 Продифференцировать функцию y(x), заданную уравнением . Решение. Продифференцируем обе части уравнения по переменной x:

     

что приводит к результату

      Пример 2 Вычислить производную функции y(x), заданной уравнением при условии y = 1. Решение. Дифференцируем обе части уравнения по x (левую часть дифференцируем как сложную функцию): 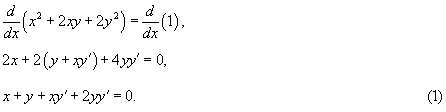  Если y = 1, то из исходного уравнения находим    

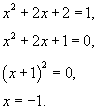
Подставим в уравнение (1) значения x = −1 и y = 1. В результате получаем

      Отсюда следует, что y' = 0 при y = 1. Пример 3 Дано уравнение окружности x ² + y ² = r ² с центром в начале координат и радиусом r. Найти производную y'(x).

Решение.

Продифференцируем по x обе части уравнения:

     

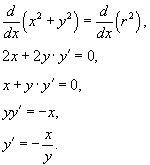
В данном случае мы можем получить и явное выражение для производной. Например, для верхней полуокружности, зависимость y(x) имеет явный вид . Отсюда находим, что производная равна       Пример 4 Найти уравнение касательной к кривой x ⁴ + y ⁴ = 2 в точке (1;1). Решение.

Продифференцируем обе части уравнения кривой по x:

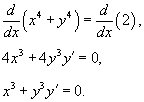      Тогда . В точке (1;1) соответственно находим, что y'(1) = −1. Следовательно, уравнение касательной в данной точке имеет вид  

37) Производная высших порядков

Понятие производной произвольного порядка задаётся рекуррентно. Полагаем

Если функция f дифференцируема в x₀, то производная первого порядка определяется соотношением

Пусть теперь производная n-го порядка f⁽ⁿ⁾ определена в некоторой окрестности точки x₀ и дифференцируема. Тогда Если функция имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от   может иметь в некоторой точке частные производные по той же или по любой другой переменной. Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными).   или  

или   Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,

38) Диф функции

Дифференциа́л (от лат. differentia — разность, различие) в математике — линейная часть приращения функции или отображения. Это понятие тесно связано с понятием производной по направлению.Обычно дифференциал f обозначается df. Некоторые авторы предпочитают обозначать шрифтом прямого начертания, желая подчеркнуть, что дифференциал является оператором. Значение дифференциала в точке x обозначается d_xf, а иногда df_x или df[x]. Если v есть касательный вектор в точке x, то значение дифференциала на v обычно обозначается df(v), в этом обозначении x излишне, но обозначения d_xf(v), df_x(v) и df[x](v) также правомерны.