1. Лабораторная работа «Изучение статистических методов обработки опытных данных»

Цель работы: изучение статистических методов обработки опытных данных: составление закона распределения случайной величины; вычисление параметров распределения; определение интервала надежности; графическое представление закона распределения.

Приборы и принадлежности: условие задачи, простой статистический ряд экспериментальных значений непрерывной случайной величины, микрокалькулятор.

В окружающем нас мире часто приходится сталкиваться с явлениями и фактами, которые при различных условиях могут происходить, а могут не происходить. Такие явления и факты называются случайными событиями. Понятие случайного события связано с единичными явлениями или их небольшим числом. При рассмотрении большого числа явлений обнаруживаются определенные закономерности (рождаемость 515 мальчиков из 1000, выпадение 6 на игральной кости, вес и рост детей, заболеваемость в отдельных регионах и т.д.).

Изучение закономерностей однородных массовых случайных явлений и составляет предмет теории вероятности и основанной на ней математической статистики.

Случайные события принято обозначать заглавными буквами латинского алфавита A, B, C, …

Возможность появления какого-либо события оценивается вероятностью наступления этого события – P(А). Классическое определение вероятности выражается формулой:

P(A) = m / n, (1)

где n – число всех единственно возможных, равновозможных и несовместимых событий, m – число событий, удовлетворяющих условиям задачи. Например, требуется определить вероятность заболевания дыхательной системы, если из 1200 обследованных пациентов у 210 были выявлены заболевания дыхательной системы. Вероятность Р(А) = 210 / 1200 = 0,175.

Изучая какое-либо явление, мы всегда имеем дело с совокупностью величин, описывающих это явление, причем каждая величина варьирует (изменяется) в различных измерениях. Такие величины называются случайными. Случайные величины принято обозначать заглавными буквами латинского алфавита: X, Y, Z,…, а их значения обозначают соответственно: x₁, x₂, x₃, …,x_i, …, x_n. Случайные величины могут быть дискретными (принимают только определенные значения в определенном диапазоне) и непрерывными (принимают любые значения в определенном диапазоне).

Представление всех возможных значений случайной величины и соответствующих им вероятностей называют законом распределения случайной величины.

Для описания распределения дискретной случайной величины используются специальные характеристики: математическое ожидание, дисперсия и среднее квадратичное отклонение.

Математическим ожиданием случайной величины является ее среднеарифметическое значение.

Оно определяется суммой произведений дозволенных значений x_i на соответствующие вероятности P_i.

M(X) = x_i P_i (2)

Дисперсией называется математическое ожидание (среднеарифмети-ческое значение) квадрата отклонения случайной величины от ее математического ожидания.

D(X) =Mx_i – M(X) ² (3)

Можно доказать, что Mx_i – M(X) ² = P_i x_i - M(X) ², поэтому на практике дисперсия определяется по формуле:

D(X) = P_i x_i - M(X) ² (4)

Среднее квадратичное отклонение случайной величины определяется как корень квадратный из дисперсии.

(X) = (5)

Определение этих характеристик производится из представления закона распределения дискретной случайной величины, в котором представлены значения случайной величины – x_i и их соответствующие вероятности – P_i.

Для непрерывной случайной величины весь диапазон измеренных значений от x_min до x_max делят на определенное число равных интервалов. Затем определяют середину каждого интервала <x_i> и вероятность попадания измеренных значений в каждый интервал:

P_i = m_i /n , (6)

где n – число всех измеренных значений, m_{i –} число значений, попадающий в каждый интервал.

Определение характеристик непрерывной случайной величины производится по тем же формулам, что и для дискретной.

Представление всех значений <x_i> и P_i и выражает закон распределения непрерывной случайной величины.

Закон распределения случайной величины может быть задан в виде таблицы, графически и аналитически (в виде формулы).

Для графического представления распределений используют главным образом два способа.

1. Построение полигона (точечной диаграммы). Для этого в системе координат x_i, P_i отмечают расчетные точки и соединяют их прямыми (рис.1а) или сглаженными линиями (рис.1б).

2. Построение столбчатой диаграммы (гистограммы). Для нее в той же системе координат строят прямоугольники, основанием которых являются значения ширины интервалов, а высотой – значения P_i для каждого интервала рис. 1(в).

рис. 1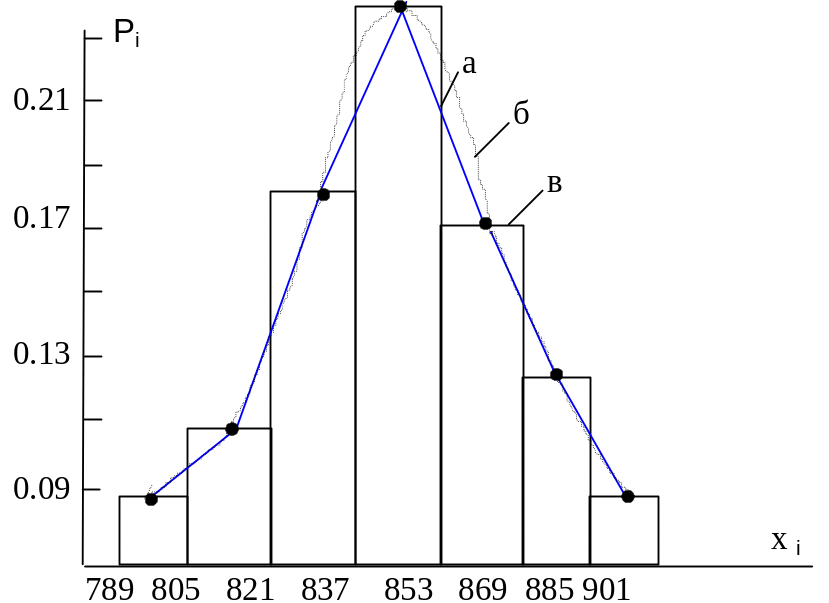

Для биологических объектов характерно то, что они в большинстве представляют однородные популяции (виды, породы, сорта, заболевания и др.). Изучение какого-либо признака у всех особей популяции дало бы множество, несколько отличающихся друг от друга значений случайной величины, характеризующей данный признак.

Множество значений случайной величины, измеренной у всех особей данной популяции, называется генеральной совокупностью.

Определить это множество практически невозможно в виду многочисленности или недоступности особей популяции. Поэтому измеряют случайную величину у части особей.

Множество значений случайной величины, измеренных у отдельных особей популяции, называют выборкой из генеральной совокупности.

Выборку можно представить в виде закона или функции распределения и определить ее основные характеристики. Обозначим - математическое ожидание выборки, - среднее квадратичное отклонение выборки, - предполагаемое математическое ожидание генеральной совокупности, его называют истинным значением измеряемой величины.

Задача статистики состоит в том, что, зная параметры выборки, оценить параметры генеральной совокупности. Конкретно, статистика ставит вопрос – определить доверительный интервал  , в который бы с достаточной степенью надежности входило истинное значение .

Надежностью результата серии измерений называется вероятность того, что истинное значение измеряемой величины попадает в выбранный доверительный интервал выборки.

Для точных физических измерений надежность равна 0,99, т.е. 99% за то, что истинное значение измеряемой величины попадет в выбранный доверительный интервал. Для биологических измерений используют надежность 0,95.

Если число измерений в выборке n  30, то доверительный интервал определяется следующим образом:

для надежности 0,95  =  2

для надежности 0,99  =  3

Если n  30, то доверительный интервал определяется по формуле

 =  t ,

где t – критерий Стьюдента, он находится по таблице Стьюдента (в любом учебнике по статистике) для надежности 0,95 – в биологических исследованиях; для надежности 0,99 – в точных физических измерениях.