3. Масштаб в проекции Гаусса — Крюгера

Перенос точек с поверхности эллипсоида на плоскость в проекции Гаусса — Крюгера происходит при следующих условиях:

1) осевой меридиан зоны изображается прямой линией, принимаемой за ось абсцисс (у = 0);

2) для точек осевого меридиана абсциссы должны быть равны соответствующим дугам, т. е. расстояниям этих точек от экватора эллипсоида, следовательно, начало прямоугольных координат — точка пересечения осевого меридиана с экватором, на проекции изображающимся прямой линией; он является осью ординат (х = 0); масштаб вдоль осевого меридиана равен единице;

3) проекция комформная, следовательно, масштабы по главным направлениям должны быть равны m=n.

На рис. 3.1 показано определение точки на поверхности эллипсоида, а на рис. 3.2 — на проекции координатами х и у.

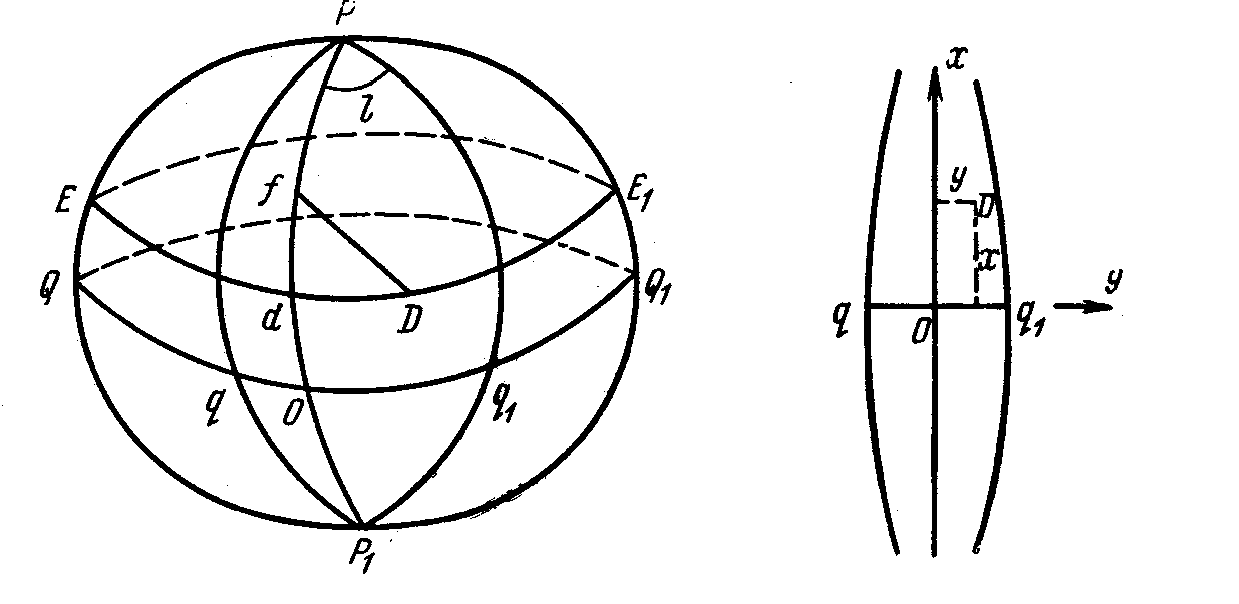
Рис. 3.1 Рис. 3.2

Указанные условия делают проекцию Гаусса — Крюгера поперечно-цилиндрической с касанием цилиндра по осевому меридиану зоны.

PfdOP₁ — осевой меридиан зоны; QqOq₁Q₁ — экватор; EdDE₁ — параллель точки D; PqP₁q₁Р — зона; дуга Odf — сфероидическая абсцисса точки D — х_с ; дуга fD — сфероическая ордината у_с точки D.

Главные направления совпадают с направлениями, параллельными сфероидическим осям координат, а в проекции — с направлениями, параллельными осям координат х и у.

Меридианы и параллели в проекции Гаусса — Крюгера, как и вообще в поперечно-цилиндрических проекциях, изображаются кривыми линиями.

Сравним проекцию Гаусса — Крюгера с поперечной цилиндрической проекцией Зольднера — Кассини. Обе проекции прямоугольные; как в той, так и в другой проекции цилиндр касается эллипсоида или шара по меридиану, который изображается в проекции прямой линией, принимаемой за ось абсцисс. В обеих проекциях для точек осевого меридиана абсциссы равны соответствующим дугам от экватора на поверхности эллипсоида или шара. Следовательно, искажения по направлениям, параллельным оси х, в этих проекциях одинаковы. Таким образом, в проекции Гаусса — Крюгера масштаб в точках по оси х, так же, как и в проекции Зольднера — Кассини, равен .

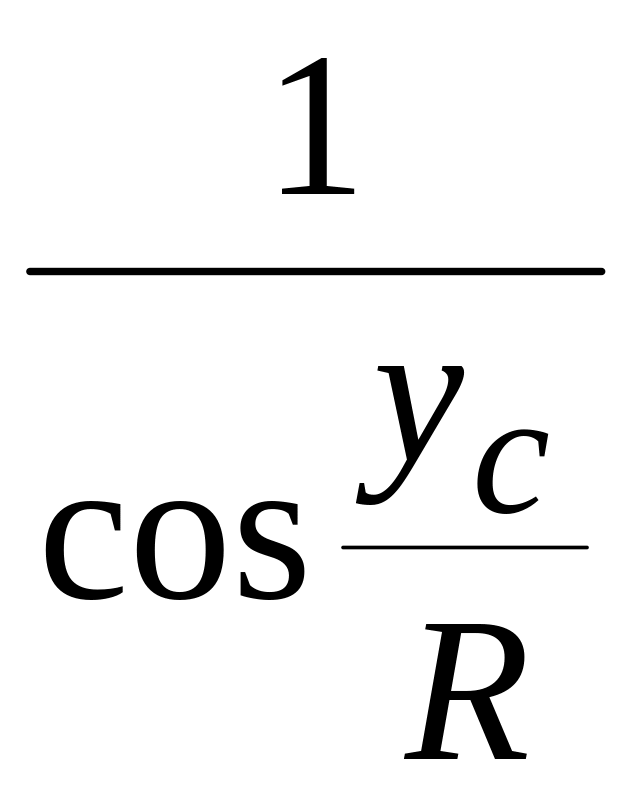Принимая в соответствии с нашим выводом радиус шара равным N, для проекции Гаусса — Крюгера находим

m = .

По условию конформности в проекции Гаусса — Крюгера масштаб по другому главному направлению, т. е. по направлению оси у, должен быть таким же, следовательно,

m = n = .

Разложим cos — в ряд и возьмем три члена ряда, тогда

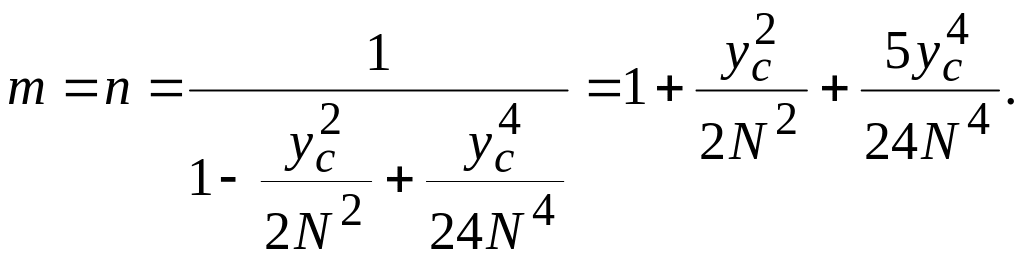(3.1)

Из (2.4: следует, что ордината у_c зависит от широты и долготы точки, поэтому масштаб в каждой точке проекции различный и искажения зависят от удаления точки от осевого меридиана зоны по оси у (табл. 3.1).

Таблица 3.1

Масштабы на краю шестиградусной зоны (при l = 3°)

Масштаб	Широта
	0°	15°	30°	45°	60°	75°	90°
m=n……….	1,0014	1,0013	1,0010	1,0007	1,0004	1,0001	1
p…………...	1,0028	1,0026	1,0020	1,0014	1,0008	1,0002	1

Искажения углов нет, поэтому ω = 0.

На рис. 3.3 изображена сетка меридианов и параллелей этой проекции.

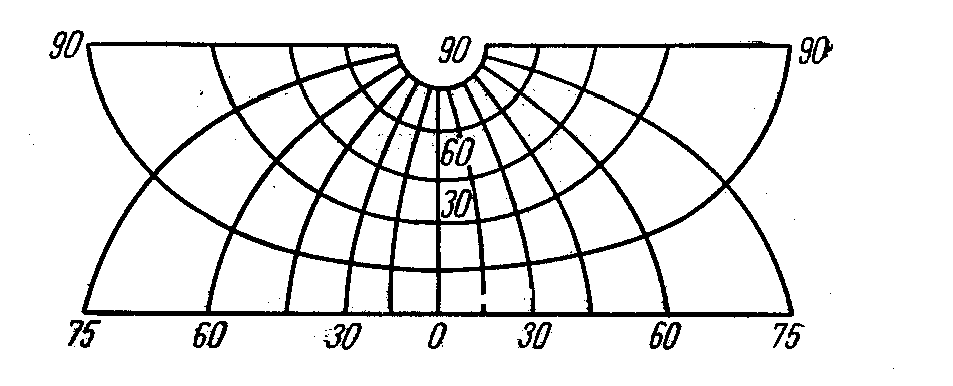
Рис. 3.3

Если бы в проекции Гаусса — Крюгера касание цилиндра происходило не по меридиану, а по экватору, то она обратилась бы в проекцию Меркатора.