
- •Miary zmienności
- •Ogólna postać tabeli korelacyjnej
- •Sposoby badania współzależności między cechami
- •Współczynnik korelacji rang spearmana
- •Kowariancje
- •Korelacja liniowa Pearsona
- •Równanie linii regresji
- •Szereg czasowy
- •Miary dynamiki zmian szeregu czasowego:
- •Jak badamy średnie tempo zmian zjawiska w czasie?
- •Indeksy cen, ilości, wartości
- •Indywidualne indeksy:
- •Zespołowe indeksy dla wszystkich absolutnych:
PODSTAWY STATYSTYKI DLA EKONOMISTOW
Statystyka – nauka o metodach ilościowych, badania zjawisk masowych. Zajmuje się badaniem procesów, jakie zachodzą w zbiorowościach statystycznych.
Zjawisko masowe – występują w przyrodzie, społeczeństwie, badane dla większej liczby przypadków, wykazują pewną prawidłowość.
Badanie statystyczne – ogół prac mających na celu:
Poznanie struktury badanej zbiorowości ze względu na określone cechy
Ocenę współzależności zjawisk
Poznanie dynamiki zmian zjawiska w czasie i przyczyn wywołujących zmienność tego zjawiska.
Populacja statystyczna (zbiorowość statystyczna) – zbiór osób, przedmiotów, zjawisk podobnych do siebie, ale nie identycznych, poddanych badaniom statystycznym. Każdy element populacji statystycznej to jednostka statystyczna.
Jednostka statystyczna – element zbiorowości statystycznej, posiada ona cechy wspólne lub przynajmniej jedną cechę wspólną z innymi jednostkami oraz różnice w stosunku do innych jednostek.
Przy określaniu populacji statystycznej określamy:
kogo, co badamy
jaki obszar obejmuje badanie
jakiego okresu dotyczy badanie
np. badamy stan zdrowia dzieci rozpoczynających naukę w 2000 roku na terenie województwa łódzkiego. W tym badaniu zbiorowością statystyczną są dzieci rozpoczynające naukę w 2000 roku. Jednostką jest każde z tych dzieci.
Badanie statystyczne ma dwojaki charakter:
całkowite (pełne, wyczerpujące) – to takie, w którym bezpośredniej obserwacji podlegają wszystkie jednostki statystyczne. Badania te przeprowadza się dla zbiorowości mało licznych, ponieważ są małe koszty. Przy tym badaniu otrzymujemy opis statystyczny.
częściowe – bezpośredniej obserwacji podlega pewien podzbiór zbiorowości statystycznej nazywany próbą i wyniki uogólniamy na całą zbiorowość. By to uogólnienie miało sens, próba musi być liczna i reprezentatywna (struktura musi być zbliżona do danej zbiorowości). Przy tym badaniu opis dotyczy próby. W częściowym odniesieniu do całej zbiorowości mamy do czynienia z wnioskowaniem statystycznym.
Cechy statystyczne - własności jednostek statystycznych podlegające badaniom. Jednocześnie cecha statystyczna jest kryterium podziału całej zbiorowości statystycznej, czyli wszystkich jednostek na mniejsze części.
Podział cech statystycznych:
mierzalne – ilościowe – wartości otrzymujemy w wyniku pomiaru lub policzenia, i które w naturalny sposób wyrażają się liczbami i występują w określony w określonych jednostkach. Dzielą się na:
skokowe (dyskretne) przyjmują wartości nie zależące od pomiaru np. liczba osób w rodzinie, dni w roku na odpoczynek
ciągłe przyjmują wartości z poziomych przedziałów. Wartości te często zależą od dokładności pomiaru (czas wykonania pewnego detalu np. długość włókna przędzy przy badaniu jej jakości)
niemierzalne – jakościowe – warianty opisujemy słowami np. zawód, wykształcenie. Dzielimy je na:
dwudzielne – istnieją dwa warianty np. płeć, tak-nie
wielodzielne – wiele wariantów np. zawód
Etapy badania statystycznego:
Projektowanie – sprecyzować cel badania, określić zbiorowość statystyczną i oszacować jej liczebność, określić charakter badania (pełne, częściowe), uściślić badane cechy, podać źródła pozyskiwania danych, przygotować formularze ankiet
Zbieranie danych statystycznych – źródła danych statystycznych są pierwotne (bezpośrednio od jednostek, obserwacje, ankieta) lub wtórne (opracowania firm, instytucji, ośrodków badań statystycznych). Dane zgromadzone są tzw. Surowe
Opracowanie danych – tabele, wykresy. Materiał należy pogrupować, usystematyzować. Grupowanie ma charakter typologiczny (gdy łączymy w grupy jednostki, które mają taki sam wariant cechy) lub wariacyjny (porządkujemy dane ze względu na wartości cechy dla tych jednostek) Pogrupowane dane zapisujemy w szeregach statystycznych
Analiza wyników – podanie informacji
Charakterystyki liczbowe struktury zbiorowości
Parametry statystyczne – są to liczby, które w systematyczny sposób opisują strukturę zbiorowości ze względu na badaną cechę mierzalną.
Parametry statystyczne dzielą się na następujące grupy:
Miary położenia
Miary zmienności
Miary asymetrii
Miary koncentracji
Miary położenia mogą być:
Klasyczne
Średnia arytmetyczna
Średnia harmoniczna
Średnia geometryczna
Inne średnie
Pozycyjne
Dominanta (moda, wartość modalna)
Kwantyle:
Kwartyle
Kwartyl dolny
Mediana
Kwartyl górny
Kwintyle
Decyle
Centyle
Miary klasyczne:
Średnia arytmetyczna określana jest wzorami:
Dla szeregu szczegółowego
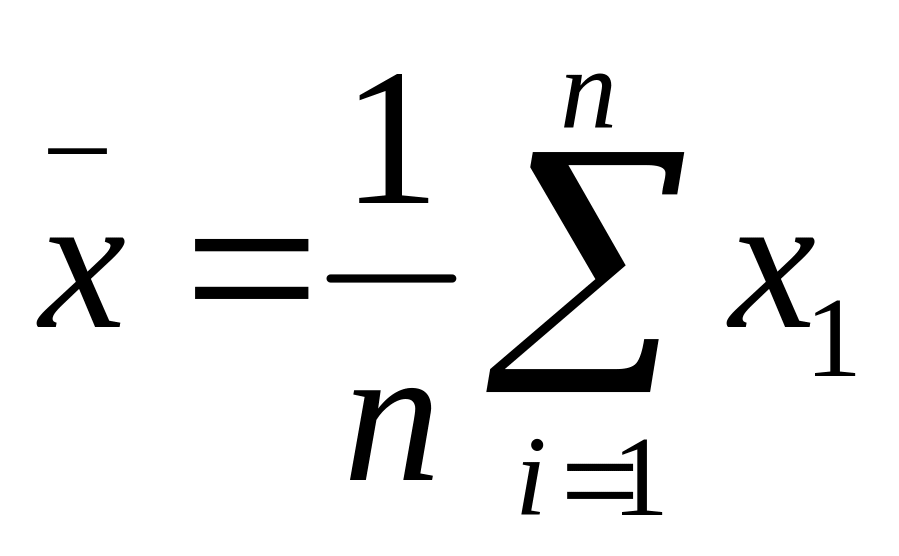
Dla szeregu rozdzielczego

Dla szeregu z przedziałem klasowym liczebność grupy
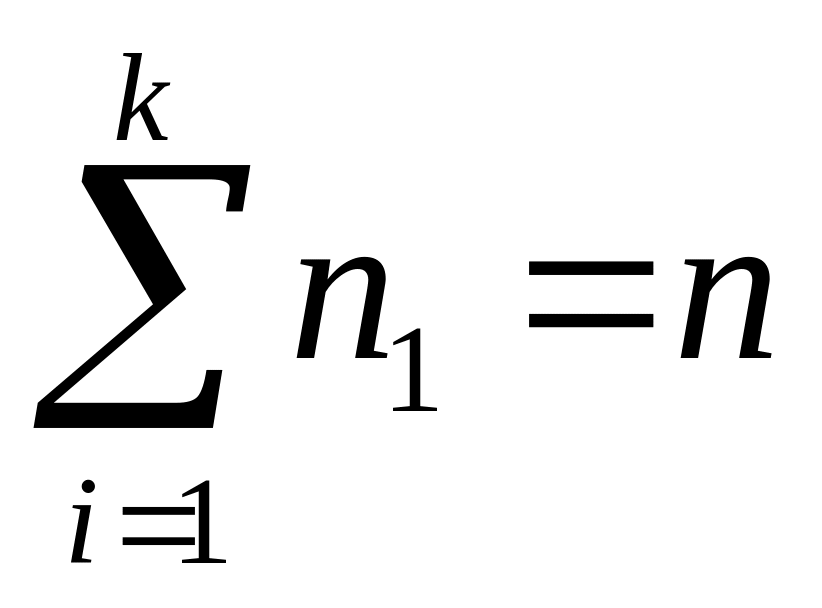
Przykład:
Badano liczbę czasopism ilustrowanych zakupionych w ciągu tygodnia przez mieszkańców pewnego bloku dane zawarto w tabeli:
Lp |
Liczba czasopism x1 |
Liczba mieszkańców n1 |
X1n1 |
Nis |
1 |
0 |
7 |
0 |
7 |
2 |
1 |
13 |
13 |
20 |
3 |
2 |
18 |
36 |
38 |
4 |
3 |
7 |
21 |
45 |
5 |
4 |
5 |
20 |
50 |
|
|
Ni=50 |
Xini=90 |
|
nis – liczebność skumulowana (dodajemy wszystkie cyfry z kolumny ni)
Szereg
punktowy
![]()
Średnio mieszkańcy tego bloku kupowali 1,8 czasopisma
Dominanta = 2 (w kolumnie xini największą liczbą jest 36 czyli liczba czasopism wynosi 2)
Mediana
-
![]()
Przykład:
Badano oszczędności mieszkańców pewnego osiedla i otrzymane wyniki przedstawiono w tabeli:
Lp |
Oszczędności w tys zł |
Liczba osób ni |
X1 |
xini |
nis |
1 |
0-2 |
8 |
1 |
8 |
8 |
2 |
2-4 |
17 |
3 |
51 |
25 |
3 |
4-6 |
12 |
6 |
60 |
37 |
4 |
6-8 |
8 |
7 |
56 |
45 |
5 |
8-10 |
5 |
9 |
45 |
50 |
|
|
50 |
|
220 |
|
Szereg
z przedziałami klasowymi:
![]()
Najliczniejsza grupa osób mająca oszczędności ok. 4,4 tys zł
Dominanta:
![]()
Własności średniej arytmetycznej
Średniej arytmetycznej nie wyznacza się dla szeregów z przedziałami klasowymi w których skrajnie przedziały są otwarte i mają stosunkowo dużą liczebność. Jeśli liczebność w skrajnych otwartych przedziałach jest stosunkowo mała, to możemy je skutecznie domknąć i wtedy obliczymy średnią arytmetyczną. Jeśli w szeregach z przedziałami klasowymi przedziały mają różne szerokości, to wzór na obliczanie średniej arytmetycznej podawany jest z pewną korektą
Średnia arytmetyczna jest dobrą miarą przeciętną tylko dla zbiorowości jednorodnych nie daje się natomiast obrazu przeciętnego poziomu cechy, gdy badana zbiorowość nie jest jednorodna np. gdy liczymy średnią płacę łącząc pracowników z różnych grup uposażenia
Średnia arytmetyczna jest większa od najmniejszej, zaś mniejsza od największej wartości w grupie
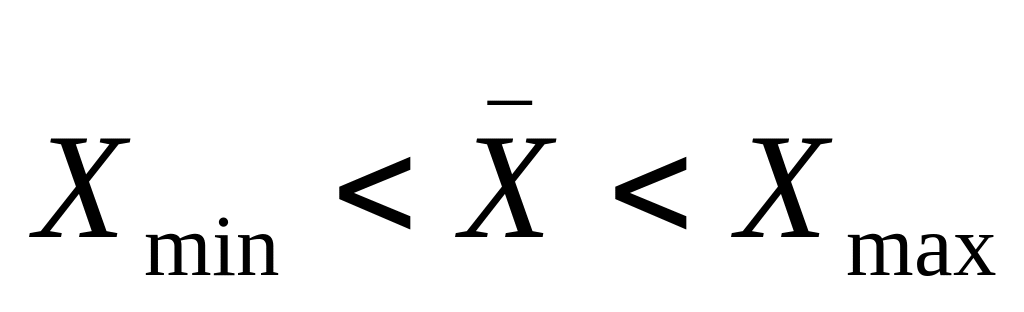
Suma odchyleń wartości cech od średniej arytmetycznej jest =0.
dla szeregu szczegółowego
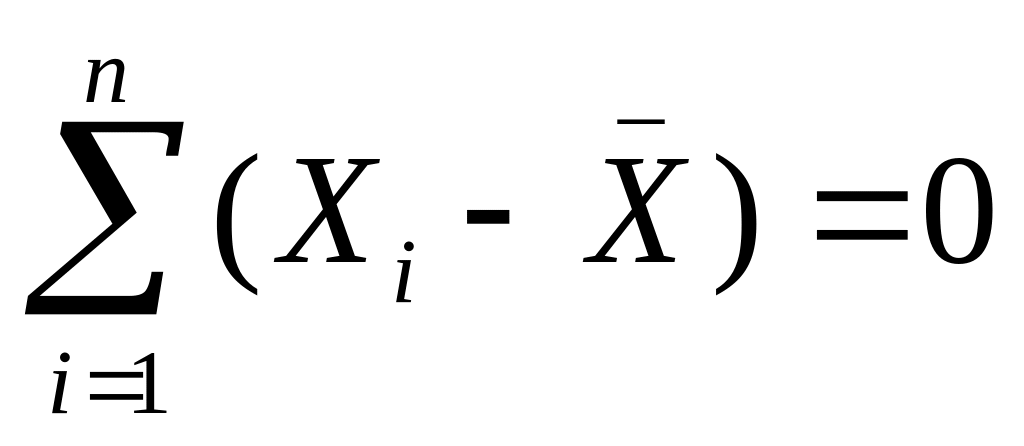
dla szeregu rozdzielczego
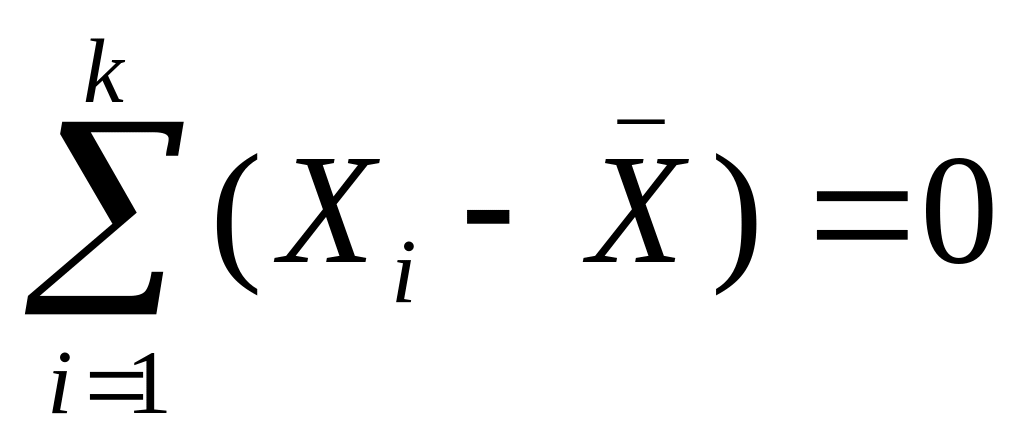
Omówienie miar pozycyjnych
Dominanta – nie istnieje w każdym szeregu, posiada ją najliczniejsza grupa
dla szeregów bez przedziałów klasowych dominantą jest taka wartość cechy, która w danym szeregu występuje największą liczbę razy o ile nie jest to wartość skrajna (najmniejsza, największa)
dla szeregów z przedziałami klasowymi dominanta istnieje jeśli wśród przedziałów klasowych występuje przedział o wyraźnie większej od innych przedziałów liczebności i szerokości zbliżonej do szerokości przedziałów z nim sąsiadujących i nie jest to przedział skrajny.
Wyznaczanie dominanty w sposób przybliżony:
GRAFICZNIE:
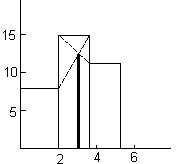
INTERPOLACYJNY
Przybliżony
![]()
gdzie:
x0 – początek przedziału dominanty
n0 – liczebność przedziału dominanty
nm-1 – liczebność przedziału stojącego nad przedziałem dominanty
nm+1 – liczebność przedziału stojącego za przedziałem dominanty
h0 – rozpiętość przedziału dominanty
Średnia arytmetyczna, dominanta i mediana traktowane są jako miary przeciętnego poziomu zjawiska.
Mediana:
Zalety mediany:
można ją wyznaczyć zawsze
nie jest miara wrażliwą na wartości skrajne
jest lepszą miarą przeciętną w sytuacji, gdy w zbiorze występują jednostki o nietypowych wartościach cechy
Wyznaczanie mediany:
Dla szeregów bez przedziałów klasowych
Me
= wartość cechy
![]() gdy „n” jest nieparzyste
gdy „n” jest nieparzyste
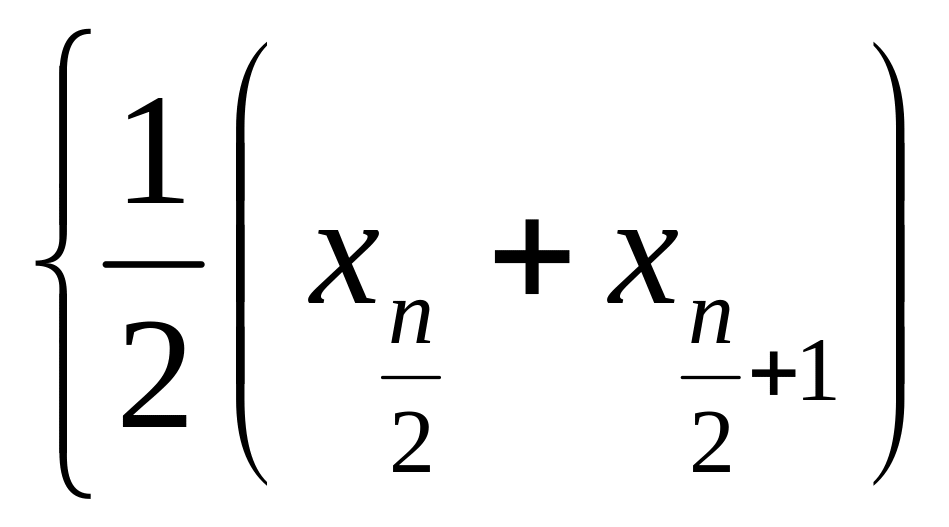 gdy
„n” jest parzyste
gdy
„n” jest parzyste
Kwartyle
Wyznaczanie:
Dla szeregów bez przedziałów klasowych
Aby wyznaczyć Q1 w szeregach bez przedziałów klasowych, bierzemy pod uwagę wszystkie wartości cechy stojące przez Me.
A jeśli Me jest elementem szeregu, to razem z tą Me i Q1 wyznaczamy tak jakby to była mediana dla tej części szeregu.
Aby wyznaczyć Q3 w szeregu bez przedziałów klasowych, bierzemy pod uwagę wszystkie wartości cechy stojące za Me.
A jeśli Me jest elementem szeregu, to razem z tą Me i Q3 wyznaczamy tak jakby to była mediana dla tej części szeregu.
Wyznaczanie mediany i kwartyli w szeregu z przedziałami klasowymi:
Wyznaczamy medianę, liczebność skumulowaną
Obliczamy
numer mediany
![]() i
sprawdzamy, w którym przedziale się mieści
i
sprawdzamy, w którym przedziale się mieści
Miary zmienności
Dzielą się na:
1. Klasyczne:
Odchylenie przeciętne
Odchylenie standardowe
Współczynniki zmienności
2. Pozycyjne:
Rozstęp szeregu
Odchylenie kwartylowe (ćwiartkowe)
Współczynniki zmienności
Miary zmienności charakteryzują stopień zróżnicowania jednostek zbiorowości pod względem badanej cechy. Miary te inaczej nazywamy miarami dyspersji lub zróżnicowania.
Współczynniki zmienności
Pozycyjne
-
![]()
Warunki te podaje się po przemnożeniu przez 100 i podajemy w procentach. Wartości tych współczynników mieszczą się w przedziale od 0 do 100 %. Im wartość bliższa 100% jest wartość współczynnika zmienności tym bardziej zróżnicowana jest badana zbiorowość pod względem analizowanej cech. Współczynniki zmienności znajdują szczególnie ważne zastosowanie w dwóch sytuacjach:
Gdy badamy kilka zbiorowości ze względu na tę samą cechę i chcemy porównać stopień zróżnicowania tych zbiorowości ze względu na tę cechę.
Gdy badamy jedną zbiorowość ze względu, na którą z tych cech zbiorowość jest najbardziej zróżnicowana.
Przykład:
Przy poprzednim podziale Polski na 49 województw badano zróżnicowanie tych województw ze względu na powierzchnię i liczbę ludności.
Otrzymano dane:
Powierzchnia (w tyś. km²) -
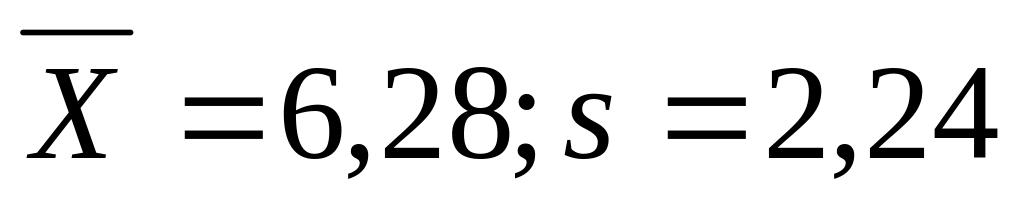
Liczba ludności (w tyś. osób) -
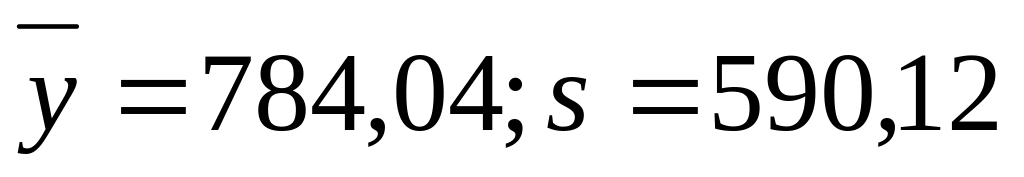
Rozwiązanie:
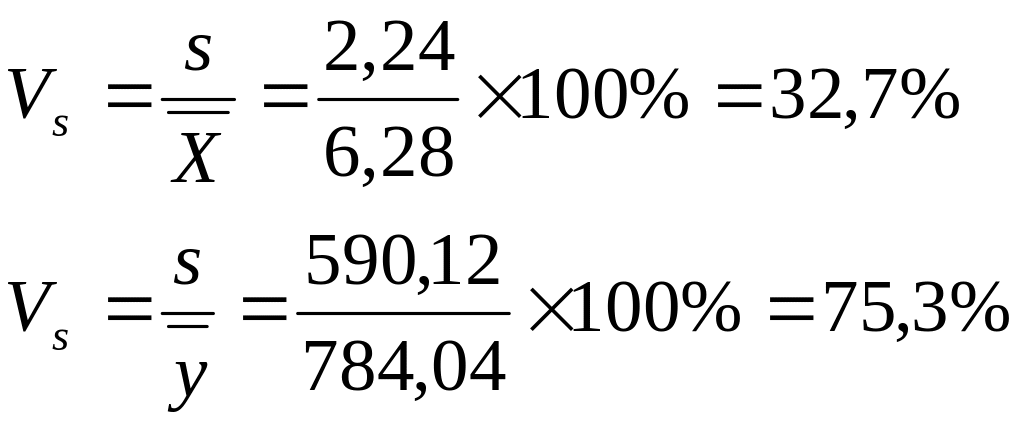
Odpowiedź:
Stopień zróżnicowania województw ze względu na liczbę ludności był znacznie wyższy niż ze względu na powierzchnię.
Przykład:
Badano liczbę czasopism ilustrowanych zakupionych w ciągu tygodnia przez mieszkańców pewnego bloku dane zawarto w tabeli:
Lp. |
Liczba czasopism
|
Liczba mieszkańców
|
|
|
|
|
|
|
|
1 |
0 |
7 |
0 |
7 |
0 |
1,8 |
12,6 |
3,24 |
22,68 |
2 |
1 |
13 |
13 |
20 |
13 |
0,8 |
10,4 |
0,64 |
8,32 |
3 |
2 |
18 |
36 |
38 |
36 |
0,2 |
3,6 |
0,04 |
0,72 |
4 |
3 |
7 |
21 |
45 |
21 |
1,2 |
8,4 |
1,44 |
0,08 |
5 |
4 |
5 |
20 |
50 |
20 |
2,2 |
11 |
4,84 |
24,2 |
|
|
|
|
90 |
|
46 |
|
66 |
|
- liczebność skumulowana (dodajemy wszystkie cyfry z kolumny )
Szereg
punktowy:
![]()
Średnio mieszkańcy tego bloku kupowali 1,8 czasopisma.
Dominanta: D = 2
Mediana:
![]()
![]()
![]()
Liczba czasopism kupowanych przez mieszkańców bloku różniła się od średniej przeciętnie o 0,92 czasopisma.
![]() =1,15
=1,15
Liczba czasopism kupowanych przez mieszkańców bloku odchyla się od średniej o 1,15 czasopisma.
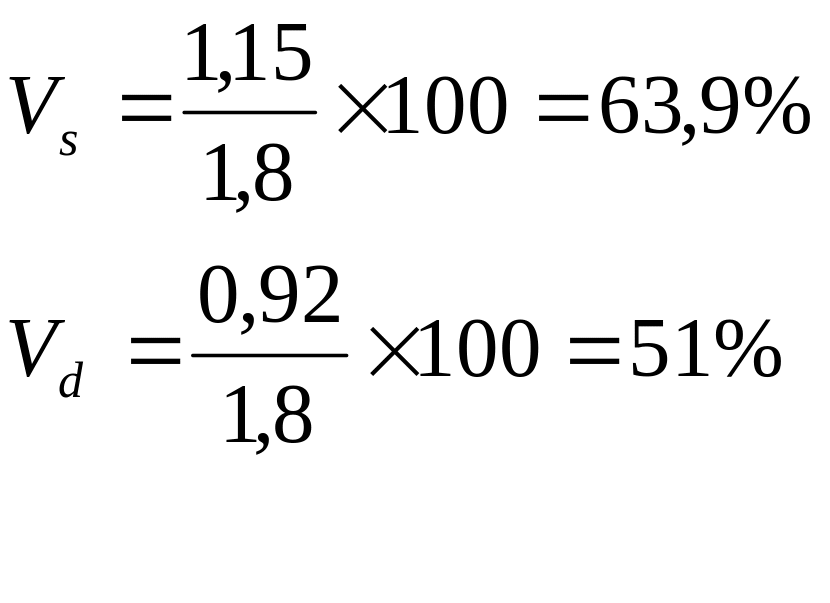
Stopień zróżnicowania mieszkańców bloku ze względu na liczbę kupowanych czasopism jest dość wysoki.
![]()
Przeciętna liczba kupowanych czasopism różniła się od mediany o 0,5.
Przykład:
Badano oszczędności mieszkańców pewnego osiedla i otrzymane wyniki przedstawiono w tabeli:
Lp. |
Oszczędności tys. zł. |
Liczba osób
|
|
|
|
|
|
|
|
1 |
0 – 2 |
8 |
1 |
8 |
8 |
3,4 |
27,2 |
11,56 |
92,48 |
2 |
2 – 4 |
17 |
3 |
51 |
25 |
1,4 |
23,8 |
1,96 |
33,32 |
3 |
4 – 6 |
12 |
6 |
60 |
37 |
0,6 |
7,2 |
0,36 |
4,32 |
4 |
6 – 8 |
8 |
7 |
56 |
45 |
2,6 |
20,8 |
6,76 |
54,08 |
5 |
8 – 10 |
5 |
9 |
45 |
50 |
4,6 |
23 |
21,16 |
105,8 |
|
50 |
|
220 |
|
|
102 |
|
290 |
|
Szereg
z przedziałami klasowymi:
![]()
Najliczniejsza grupa osób mająca oszczędności ok. 4,4 tys. zł.
Dominanta:
![]()
![]()
Oszczędności mieszkańców osiedla różniły się przeciętnie średnio o 2,04 tyś. zł.
![]() =2,408
tyś. zł.
=2,408
tyś. zł.
Oszczędności mieszkańców osiedla odchylają się od średniej przeciętnie o 2408 zł.
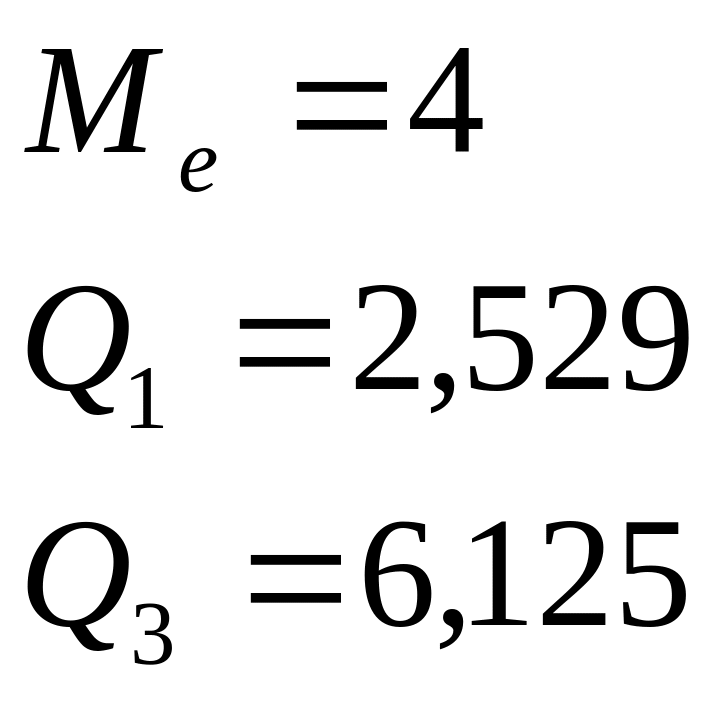
![]()
Oszczędności mieszkańców osiedla różniły się od mediany o 1798 tyś. zł.
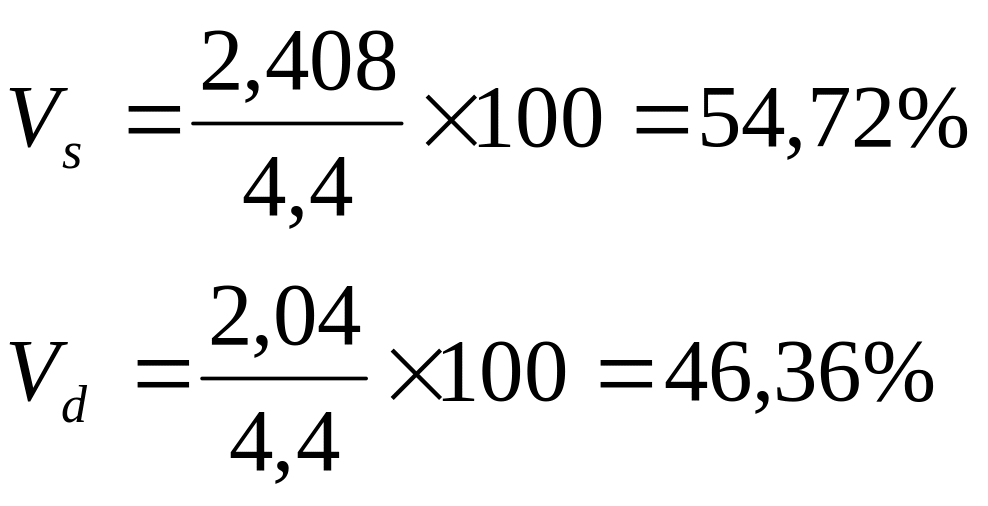
Stopień zróżnicowania mieszkańców osiedla ze względu na oszczędności jest dość wysoki.
Przykład:
Badano zarobki pracowników w trzech zakładach ABC i otrzymano dane:
|
A |
B |
C |
|
0,9 tyś zł |
0,9 tyś zł |
0,9 tyś zł |
|
0,9 tyś zł |
0,88 tyś zł |
0,92 tyś zł |
|
0,9 tyś zł |
0,75 tyś zł |
1,05 tyś zł |
|
|
|
|
![]() -
jest
to szereg statystyczny, gdzie zachodzi równość tych miar jest to
szereg symetryczny. Szereg symetryczny przedstawia grupę jednostek
statystycznych mających takie same wartości cechy jak średnia.
-
jest
to szereg statystyczny, gdzie zachodzi równość tych miar jest to
szereg symetryczny. Szereg symetryczny przedstawia grupę jednostek
statystycznych mających takie same wartości cechy jak średnia.
- asymetria prawostronna dodatnia przy tej asymetrii najliczniejsza grupa jednostek mająca wartości cechy poniżej średniej.
- asymetria lewostronna ujemna najliczniejsza grupa jednostek statystycznych mająca wartości cechy większe niż średnia.
Wskaźniki skośności
Kierunek
asymetrii mierzy wskaźnik
skośności:
![]()
Szereg symetryczny -
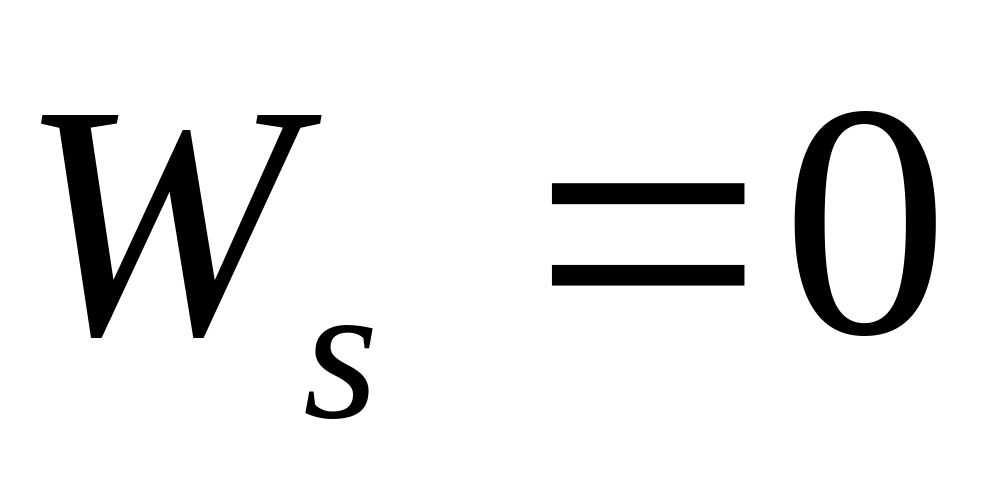
Asymetria prawostronna -
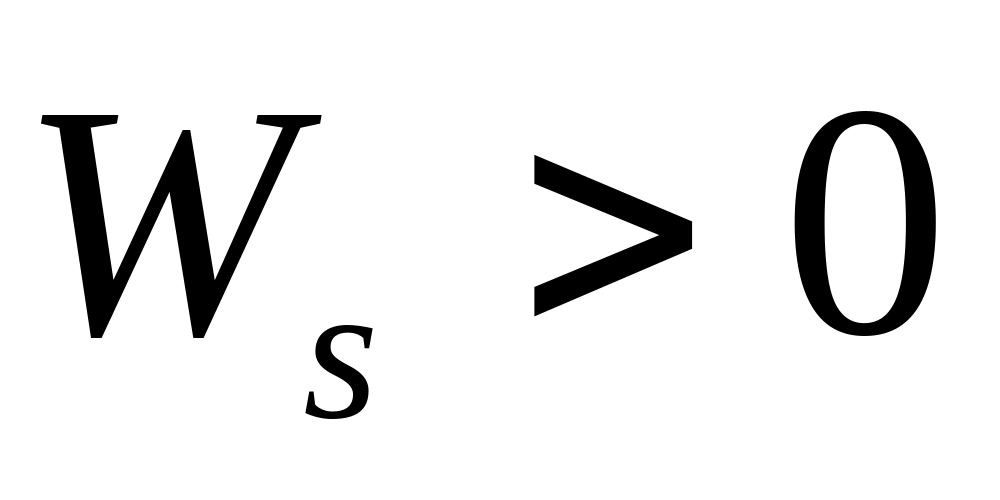
Asymetria lewostronna -
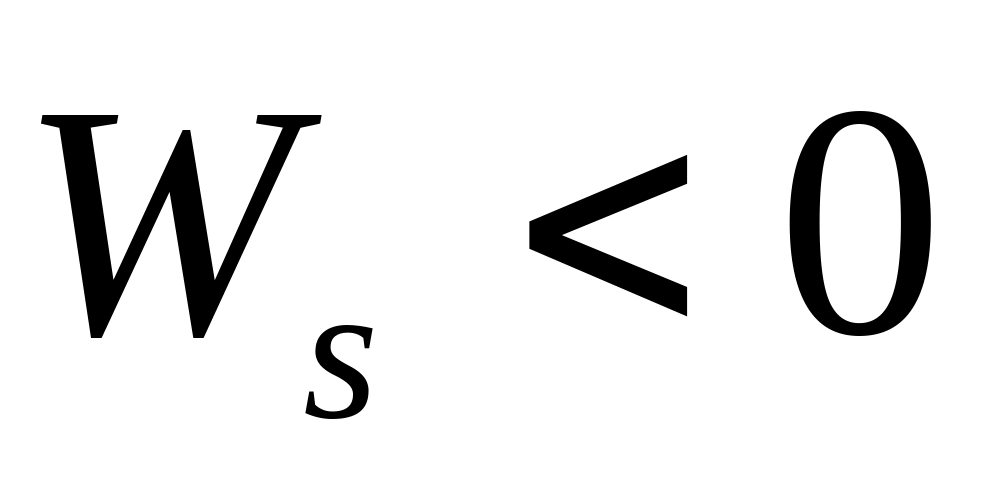
Kierunek
i siłę asymetrii mierzy współczynnik
skośności:

![]()
W przypadku skrajnej asymetrii współczynnik ten może znaleźć się za tymi granicami.
Badanie zbiorowości ze względu na dwie cechy
Przy badaniu zbiorowości ze względu na dwie cechy dane dotyczące tych cech porządkujemy w następujący sposób: gdy liczba obserwacji jest mała budujemy szereg szczegółowy.
Np.: przebadano 6 firm zajmujących się usługami porządkowymi, porównując ich miesięczne wydatki na reklamę.
X – wydatki na reklamę ( w tyś zł)
Y – dochody (w tyś zł)
Lp. |
Wydatki na reklamę |
Dochody |
1 |
1,5 |
10 |
2 |
2 |
20 |
3 |
2,5 |
20 |
4 |
2,5 |
15 |
5 |
4,5 |
25 |
6 |
5 |
30 |
Przykład:
W grupie 50 studentów badano oceny z matematyki X i statystyki Y
(2,2) – 10 osób, (2,3) – 5 osób, (3,2) – 12 osób, (3,3) – 8 osób
( 4,3)
- , (4,4) – 5 osób, (4,5) – 6 osób, (5,5) –
4 osoby
4,3)
- , (4,4) – 5 osób, (4,5) – 6 osób, (5,5) –
4 osoby
Budujemy tabelę korelacyjną
Oceny z matematyki |
Oceny ze statystyki |
|
|||
2 |
3 |
4 |
5 |
||
2 |
10 |
5 |
|
|
15 |
3 |
12 |
8 |
|
|
20 |
4 |
|
|
5 |
6 |
11 |
5 |
|
|
|
4 |
4 |
|
22 |
13 |
5 |
10 |
|
![]() -
rozkład brzegowy cechy X,
-
rozkład brzegowy cechy X,
![]() -
rozkład brzegowy cechy Y
-
rozkład brzegowy cechy Y
