
- •Введение.
- •Логическая структура современной физики.
- •Границы применимости физической теории.
- •Глава 1. Основные понятия и законы классической механики.
- •§2. Классические представления о пространстве и времени и их арифметизация.
- •§3. Кинематические и динамические характеристики механического движения.
- •§4. Законы динамики Ньютона.
- •§5. Принцип относительности Галилея.
- •§ 6. Основная задача динамики и роль начальных условий. Принцип причинности классической механики.
- •§ 7. Потенциальная энергия и классификация свободных механических систем.
- •Глава. 2. Законы сохранения и принцип симметрии.
- •§ 8. Первые интегралы уравнений движения и законы сохранения.
- •§ 9. Закон сохранения энергии и его связь с однородностью времени.
- •§ 10. Закон сохранения импульса и его связь с однородностью пространства.
- •§ 11. Закон сохранения момента импульса и его связь с изотропностью пространства.
- •Глава 3. Основы аналитической механики.
- •§ 12. Постановка задачи о движении несвободной механической системы. Классификация связей.
- •13. Уравнения Лагранжа. Функция Лагранжа.
- •С учетом (13.12) перепишем уравнения (13.11) в окончательном виде
- •§ 14. Функция Лагранжа и законы сохранения.
- •§ 15. Основная задача вариационного исчисления. Уравнения Эйлера.
- •Простейшим функционалом является криволинейный интеграл
- •Интегрируя второй интеграл в правой части (15.6) по частям с учетом предельных условий (15.4) получаем:
- •Обобщим полученные результаты для функционала
- •§ 16. Принципы наименьшего действия Гамильтона-Остроградського.
- •§ 17. Канонические уравнения движения.
- •Подставляя (17.8) в (17.7), получаем
- •§ 18. Скобоки Пуассона.
- •§ 19. Уравнение Гамильтона-Якоби.
§2. Классические представления о пространстве и времени и их арифметизация.
Движение материальных объектов происходит в пространстве и во времени. Поэтому представления о пространстве и времени являются основными понятиями не только классической механики, но и всей физики. Эти понятия отражают порядок расположения одновремéнно сосуществующих объектов (пространство) и последовательность существования сменяющих друг друга явлений (время). Материализм подчеркивает объективный характер пространства и времени, отрицает вневременнýю и внепространственную реальность. Пространство и время неотделимы от материи. В єтом проявляется их универсальность и всеобщность. Диалектический материализм признает не просто внешнюю связь времени и пространства с движущейся материей, а считает, что это движение является сущностью времени и пространства (т.е. свойства их полностью зависят от свойств движущейся материи) и что, следовательно, материя, движение, пространство и время неотделимы друг от друга. Отметим здесь, что именно эти идеи получают все более полное подтверждение в современной ФКМ.
Однако, в классической механике (и во всей МКМ) количественно реализована не диалектико-материалистическая, а метафизическая концепция, согласно которой время и пространство существуют независимо от материальных процессов и отдельно друг от друга. Другими словами, в основе МН лежат наиболее примитивные представления о пространстве и времени, полученные в результате обобщения наблюдений только медленных движений макроскопических тел в условиях Земли. Отсюда следует, что эволюция, а на некоторых этапах даже коренная ломка этих классических представлений о пространстве и времени настолько же закономерны, сколь закономерен сам процесс развития физики.
Для количественного описания движения тел необходимо предварительно арифметизировать пространство и время и получить тем самым возможность выражать любые пространственные и временные соотношения с помощью чисел. Для этого (помня о том, что физика - наука экспериментальная) требуется указать: 1) способ измерения расстояний между материальными точками (это можно осуществить с помощью тех или иных эталонов длины); 2) способ измерения интервалов между различными моментами времени (для этого надо иметь какие-нибудь часы, т.е. прибор, действие которого основана на использовании некоторого периодического процесса, протекающего равномерно и независимо от других явлений природы); 3) ту или другую систему координат, связанную с телом отсчета (относительно которого описывается механическая форма движения). Совокупность системы координат и часов, связанных с телом отсчета, называется системой отсчета (СО) в механике. Т.о., пользуясь в дальнейшем понятием «СО», мы будем всегда подразумевать вполне определенный способ арифметизации пространства и времени и способ измерения пространственных и временных интервалов.
При этом в классической механике постулируются следующие свойства пространства и времени:
1) пространство является трехмерным многообразием (в математическом понятии "многообразие" закодировано важнейшее постулируемое свойство пространства - его непрерывность, что позволяет рассматривать сколь угодно малые, даже бесконечно малые, интервалы в просторные и, следовательно, использовать всю мощь математического анализа; 3х - мерность означает, что положение любой геометрической точки в просторные можно задать в произвольной системе координат тремя числами);
2) пространство однородно, т.е. в нем отсутствуют чем-либо примечательные точки, которые могут быть выделены среди всех точек (все точки пространства равноправны);
3) пространство изотропно, т.е. в нем отсутствуют чем-либо примечательные направления, которые могут быть выделены среди всех направлений (все направления в пространстве равноправны);
4) пространство является евклидовым, т.е. его метрические свойства полностью описываются системой аксиом геометрии Евклида;
5) пространство абсолютно в том смысле, что все его перечисленные выше свойства никак не связанны со свойствами времени и полностью независимы от протекающих в пространстве физических процессов. В частности, этим постулатом утверждается абсолютность пространственных интервалов (т.е. одинаковость расстояний между двумя материальными точками m1 и m2 в данный момент времени "с точки зрения" всех СО), что в декартовой системе координат можно записать так:
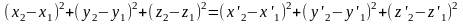 ,
(2.1)
,
(2.1)
или для расстояний между двумя бесконечно близкими точками:
 ,
(2.1')
,
(2.1')
где штрихами отмечены координаты тех же точек в другой С).
6) время является одномерным многообразием (т.е., оно непрерывно и для задания любого момента времени необходимо только одно число);
7) время однородно, т.е. нет чем-либо примечательных, выделенных моментов времени (все моменты времени равноправны);
8) время абсолютно, т.е. во всех точках пространства оно «течет» одинаково равномерно и это его «течение» не зависит от движения материальных тел и физических процессов. В частности, этим постулатом утверждается абсолютность временных интервалов между событиями, т.е. принимается, что продолжительность любого процесса одинакова во всех СО, движущихся друг относительно друга произвольным образом, т.е.
 или
или
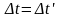 (2.2)
(2.2)
где
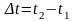 и
и
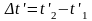 -
продолжительность одного и того же
процесса в двух различных СО. Для процесса
бесконечно малой продолжительности
(2.2) записывается в виде
-
продолжительность одного и того же
процесса в двух различных СО. Для процесса
бесконечно малой продолжительности
(2.2) записывается в виде
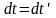 (2.2')
(2.2')
Согласно (2.2) во всех СО можно произвольным образом выбрать одно и то же начало отсчета времени и ввести во всех СО единую временнýю координату t, т.е. фактически здесь постулируется существование таких часов, период которых не зависит от характера их движения и не изменяется при переносе из одной произвольно движущейся СО в другую.
Замечание. Перечисленные постулаты о конкретных свойствах пространства и времени справедливы только в классической механике (шире - в МКМ). Современное развитие физики установило несправедливость постулатов 2) - 5) и 7) - 8); сомнению в ЕКТП поддаются даже постулаты 1) и 6).
