§ 19. Уравнение Гамильтона-Якоби.
Для формулировки принципа наименьшего действия Гамильтона-Остроградского мы в § 16 определили действие S механической системы как определенный интеграл
, (19.1)
зависящий от вида конфигурационных траекторий системы, начинающихся и заканчивающихся в двух заданных конфигурациях и в заданные моменты времени и (см. рис. 16.1)).
Возможна, однако, и постановка таких физических задач, когда действительные движения системы могут:
1) “оканчиваться” в разных конфигурациях ,
2) совершаются из одной конфигурации в другую за разные промежутки времени .
Таковыми являются
задачи, связанные с рассмотрением
множества различных действительных
движений системы, которые отличаются
друг от друга различным выбором ее
начального состояния (точнее,
различным выбором ее обобщенных
начальных скоростей
при одинаковой начальной конфигурации
– см. рис. (16.1)). Так как при такой постановке
задач все изучаемые движения системы
являются действительными, то все
рассматриваемые при этом конфигурационные
траектории автоматически удовлетворяют
уравнениям Лагранжа (13.18). Т.о., в самом
общем случае (учитывающем и изложенную
выше возможность постановки физических
задач), понятие о действии механической
системы (19.1) следует обобщить и
рассматривать действие
как явную функцию
конечного момента времени
и конечной конфигурации системы
,
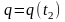т.е. действие системы в общем случае
можно определить неопределенным
интегралом
. (19.2)
Используя (17.3), (19.2) можно переписать в виде (см. также (17.6))
, (19.3)
откуда для полного
дифференциала
получаем выражение
. (19.4)
С другой стороны,
формальное выражение для полного
дифференциала от функции
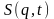имеет вид
. (19.5)
Из сравнения (19.4) и (19.5) находим:
(19.6)
,
(19.7)
Если теперь в соотношении (19.6) обобщенные
импульсы
,
входящие в функцию Гамильтона, заменить
согласно (19.7) частными производными
,
то мы получим уравнение
, (19.8)
которому должна
удовлетворять функция действия
механической системы с обобщенно-потенциальными
активными силами и голономными идеальными
связями. Это уравнение в частных
производных первого порядка называется
уравнением Гамильтона-Якоби. Оно
является нелинейным уравнением,
т.к. частные производные
входят в него во второй степени. Например,
для свободной материальной точки массы
,
движущейся в потенциальном поле
,
функция Гамильтона имеет вид
;
поэтому уравнение Гамильтона-Якоби
(19.8) для такой системы записывается в
виде (если в качестве обобщенных координат
точки использовать ее декартовые
координаты):
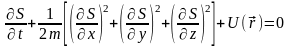. (19.9)
Наряду с методом Лагранжа и Гамильтона уравнение (19.8) составляет основу еще одного метода интегрирования уравнения движения, который здесь не излагается.
Важное значение уравнения Гамильтона-Якоби (19.8) состоит в том, что оно помогает: 1) вскрыть аналогию между классической механикой частицы и волновым процессом (т.н. оптико-механическую аналогию), играющую важную роль при объяснении волновых свойств микрочастиц в квантовой механике; 2) установить предельный переход от квантовой механики к механике классической (см. часть IV).
Заключительное замечание. Аналитические методы исследования механического движения, изложенные в главе 3, развиты на основе механической картины мира, т.е. на основе примитивных (с современной точки зрения) представлений о физической форме движения материи, и поэтому, на первый взгляд, не могут быть использованы за пределами МКМ. Однако, как мы уже неоднократно подчеркивали, эти методы при соответствующем их обобщении с большим успехом применяются и в рамках других ФКМ – ЭМКС и КПКМ. Это обстоятельство отчетливо подтверждает единство физической реальности и является убедительной естественно научной иллюстрацией положения диалектического материализма о единстве материального мира. Это же обстоятельство дает убедительный ответ на вопрос, почему серьезное изучение «древней» науки – классической механики совсем необходимо для воспитания современного физика-исследователя.