
- •Введение.
- •Логическая структура современной физики.
- •Границы применимости физической теории.
- •Глава 1. Основные понятия и законы классической механики.
- •§2. Классические представления о пространстве и времени и их арифметизация.
- •§3. Кинематические и динамические характеристики механического движения.
- •§4. Законы динамики Ньютона.
- •§5. Принцип относительности Галилея.
- •§ 6. Основная задача динамики и роль начальных условий. Принцип причинности классической механики.
- •§ 7. Потенциальная энергия и классификация свободных механических систем.
- •Глава. 2. Законы сохранения и принцип симметрии.
- •§ 8. Первые интегралы уравнений движения и законы сохранения.
- •§ 9. Закон сохранения энергии и его связь с однородностью времени.
- •§ 10. Закон сохранения импульса и его связь с однородностью пространства.
- •§ 11. Закон сохранения момента импульса и его связь с изотропностью пространства.
- •Глава 3. Основы аналитической механики.
- •§ 12. Постановка задачи о движении несвободной механической системы. Классификация связей.
- •13. Уравнения Лагранжа. Функция Лагранжа.
- •С учетом (13.12) перепишем уравнения (13.11) в окончательном виде
- •§ 14. Функция Лагранжа и законы сохранения.
- •§ 15. Основная задача вариационного исчисления. Уравнения Эйлера.
- •Простейшим функционалом является криволинейный интеграл
- •Интегрируя второй интеграл в правой части (15.6) по частям с учетом предельных условий (15.4) получаем:
- •Обобщим полученные результаты для функционала
- •§ 16. Принципы наименьшего действия Гамильтона-Остроградського.
- •§ 17. Канонические уравнения движения.
- •Подставляя (17.8) в (17.7), получаем
- •§ 18. Скобоки Пуассона.
- •§ 19. Уравнение Гамильтона-Якоби.
13. Уравнения Лагранжа. Функция Лагранжа.
В этом параграфе мы изложим такой способ решения основной динамической задачи для связанных механических систем, который не содержит недостатков способа изложенного в § 12. Основная идея состоит в том, чтобы общую динамическую задачу об отыскании закона движения системы и сил реакции связей разбить (расчленить) на две задачи: 1) найти сначала закон движения системы (эту задачу в дальнейшем мы и будем называть основной); для этого необходимо получить замкнутую систему уравнений для S =3n-k независимых координат системы (с помощью которых можно задать состояние связанной системы в любой момент времени); 2) затем с помощью уравнений (12,11) определить и неизвестные , если в этом есть необходимость (эта задача тривиальная по сравнению с первой, так как ее решение сводится к взятию вторых производных по временем от координат, что всегда выполнимо). В дальнейшем мы будем решать только основную задачу нахождения закона движения связанной механической системы, состоящей из n материальных точек, на которые наложено k идеальных, удерживающих голономных связей. Необходимые для решения этой задачи уравнения движения можно получить последовательным исключением из системы уравнений Ньютона (12,11) сначала неизвестных сил реакций связей , а затем и зависимых координат связанной системы.
Для исключения сил реакций связей, умножим скалярно каждое из уравнений движения (12,11) на виртуальное перемещение соответствующей точки и сложим почленно результаты умножения. Получаем уравнение
 (13,1)
(13,1)
В силу условия идеальности связей (12,10) последняя сумма в (13,1) равняется нулю, поэтому перепишем (13,1) в виде
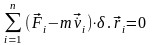 .
(13,2)
.
(13,2)
Уравнение
(13,2) представляет собой математическую
формулировку одного из важнейших
дифференциальных
вариационных принципов механики
– принципа
Д’Аламбера–Лагранжа,
который утверждает: если на механическую
систему наложены удерживающие, голономные
и идеальные связи, то в каждый момент
времени сумма виртуальных работ всех
активных сил
и так называемых “сил инерции” Д’Аламбера
 равняется нулю для любого виртуального
перемещения системы. Уравнение (13,2)
называют так же общим
уравнением динамики голономных систем,
так как его можно принять в качестве
основной и единственной аксиомы для
построения теории движения таких систем
(из него можно получить любые другие
уравнения движения, т.е. как уравнения
Ньютона, так и уравнения Лагранжа).
равняется нулю для любого виртуального
перемещения системы. Уравнение (13,2)
называют так же общим
уравнением динамики голономных систем,
так как его можно принять в качестве
основной и единственной аксиомы для
построения теории движения таких систем
(из него можно получить любые другие
уравнения движения, т.е. как уравнения
Ньютона, так и уравнения Лагранжа).
Уравнение (13,2) содержит вариации как независимых, так и зависимых координат связанной системы, так как на ее наложена k связей вида (12,2). Поэтому для получения из (13,2) дифференциальных уравнений движения необходимо исключить из этого уравнения вариации зависимых координат, т.е. перейти к независимым (или, как говорят, обобщенным) координатам механической системы.
Обобщенными
(или независимыми)
координатами
механической системы называют любые
3n-k величин
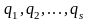 (число которых совпадает с числом
степеней воли системы s=3n-k), однозначно
определяющих положение
системы в пространстве в любой момент
времени. Из этого определения следует,
что обобщенные координаты должны
удовлетворять следующим двум требованиям:
(число которых совпадает с числом
степеней воли системы s=3n-k), однозначно
определяющих положение
системы в пространстве в любой момент
времени. Из этого определения следует,
что обобщенные координаты должны
удовлетворять следующим двум требованиям:
Декартовые координаты точек должны быть однозначными функциями обобщенных координат вида
 ,
(13,3)
,
(13,3)
если на систему наложенные нестационарные связи, или связи вида
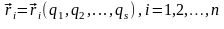 ,
(13,4)
,
(13,4)
если на систему наложенные стационарные связи.
Обобщенные координаты необходимо выбирать в полном соответствии с наложенными на систему связями. Это означает, что уравнения связей (12,2) должны обращаться в тождества при подстановке в них функций (13,3) или (13,4).
Поясним сказанное на примере сферического маятника, рассмотренного в § 12. Для этой системы n=1, k=1, поэтому s=3n–k=2, т.е. положение маятника можно задать с помощью двух обобщенных координат, в качестве которых можно выбрать сферические координаты θ и φ. При этом декартовые координаты однозначно выражаются через θ и φ:
 ,
(13,5)
,
(13,5)
а уравнение связи (12,17) обращается в тождество при подстановке в него функции (13,5), что легко проверить.
Замечание.
В §6 мы видели, что состояние
свободной
системы в любой момент времени определяется
одновременным
заданием ее декартовых координат
 и декартовых компонент скоростей точек
и декартовых компонент скоростей точек
 .
Аналогично, состояние
связанной
системы в любой момент времени полностью
определяется одновременным
заданием
ее обобщенных
координат
и обобщенных
скоростей
.
Аналогично, состояние
связанной
системы в любой момент времени полностью
определяется одновременным
заданием
ее обобщенных
координат
и обобщенных
скоростей
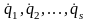 .
Ясно, что физически такое определение
состояния системы основано на допущении
о возможности одновременного
точного измерения у макроскопических
тел любых физических величин (см. §6).
.
Ясно, что физически такое определение
состояния системы основано на допущении
о возможности одновременного
точного измерения у макроскопических
тел любых физических величин (см. §6).
Выпишем здесь ряд формул, которыми мы в дальнейшем воспользуемся, описывая переход от декартових координат к обобщенным. Для виртуальных перемещений из (13,3) имеем
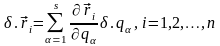 , (13,5)
, (13,5)
где
 - вариации обобщенных (независимых)
координат. Связь между скоростями точек
- вариации обобщенных (независимых)
координат. Связь между скоростями точек
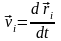 и их обобщенными
скоростями
и их обобщенными
скоростями
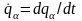 получаем, дифференцируя (13,3) по времени:
получаем, дифференцируя (13,3) по времени:
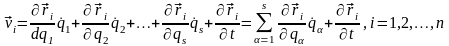 .
(13,6)
.
(13,6)
Так
как согласно (13,6) скорости
являются линейные
функции обобщенных скоростей
 ,
то беря частные производные по
от соотношений (13,6), получаем тождества
,
то беря частные производные по
от соотношений (13,6), получаем тождества
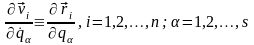 .
(13.7)
.
(13.7)
Дале,
учитывая, что
 есть функции обобщенных координат
есть функции обобщенных координат
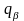 и времени t , и используя (13,6) получаем:
и времени t , и используя (13,6) получаем:
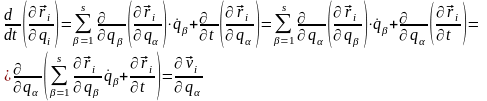
т.е. окончательно имеем тождества
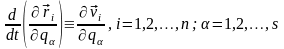 .
(13,8)
.
(13,8)
Перейдем теперь в уравнении (13,2) к обобщенным координатам. Подставляя в (13,2) выражения (13,5) и изменяя порядок выполнения операций суммирования по индексам i и α , получаем
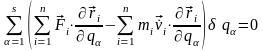 (13,9)
(13,9)
Введем обозначение
 (13,10)
(13,10)
и
назовем скалярную
величину
 обобщенной
силой,
соответствующей независимой координате
обобщенной
силой,
соответствующей независимой координате
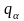 .
Так как виртуальные перемещения
независимы,
то все коэффициенты при всех перемещениях
в левой части равенства (13,9) должны
обращаться в нуль, т.е. с учетом (13,10)
имеем уравнения
.
Так как виртуальные перемещения
независимы,
то все коэффициенты при всех перемещениях
в левой части равенства (13,9) должны
обращаться в нуль, т.е. с учетом (13,10)
имеем уравнения
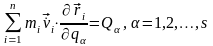 . (13,11)
. (13,11)
Это
и есть, по сути дела, искомые уравнения
движения в обобщенных координатах, где
и
согласно (13,3) и (13,6) следует рассматривать
как функции обобщенных координат и
скоростей:
 ,
,
 .
Здесь и в дальнейшем мы воспользуемся
сокращенными обозначениями:
.
Здесь и в дальнейшем мы воспользуемся
сокращенными обозначениями:
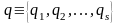 и
и
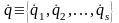 .
Для лучшего понимания физического
смысла величины, состоящей в левой части
(13,11), проделаем с ней ряд тождественных
преобразований. Прежде всего заметим,
что
.
Для лучшего понимания физического
смысла величины, состоящей в левой части
(13,11), проделаем с ней ряд тождественных
преобразований. Прежде всего заметим,
что
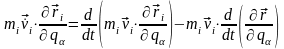 ,
,
откуда с учетом тождеств (13,7) – (13,8) получаем
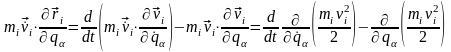
и, следовательно,
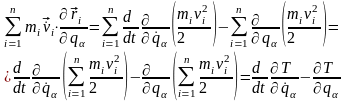 (13.12)
(13.12)
где
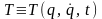 - кинетическая
энергия системы,
представленная как функция обобщенных
координат
- кинетическая
энергия системы,
представленная как функция обобщенных
координат
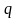 ,
обобщенных скоростей
,
обобщенных скоростей
 и времени
и времени
 .
.
