
- •Введение.
- •Логическая структура современной физики.
- •Границы применимости физической теории.
- •Глава 1. Основные понятия и законы классической механики.
- •§2. Классические представления о пространстве и времени и их арифметизация.
- •§3. Кинематические и динамические характеристики механического движения.
- •§4. Законы динамики Ньютона.
- •§5. Принцип относительности Галилея.
- •§ 6. Основная задача динамики и роль начальных условий. Принцип причинности классической механики.
- •§ 7. Потенциальная энергия и классификация свободных механических систем.
- •Глава. 2. Законы сохранения и принцип симметрии.
- •§ 8. Первые интегралы уравнений движения и законы сохранения.
- •§ 9. Закон сохранения энергии и его связь с однородностью времени.
- •§ 10. Закон сохранения импульса и его связь с однородностью пространства.
- •§ 11. Закон сохранения момента импульса и его связь с изотропностью пространства.
- •Глава 3. Основы аналитической механики.
- •§ 12. Постановка задачи о движении несвободной механической системы. Классификация связей.
- •13. Уравнения Лагранжа. Функция Лагранжа.
- •С учетом (13.12) перепишем уравнения (13.11) в окончательном виде
- •§ 14. Функция Лагранжа и законы сохранения.
- •§ 15. Основная задача вариационного исчисления. Уравнения Эйлера.
- •Простейшим функционалом является криволинейный интеграл
- •Интегрируя второй интеграл в правой части (15.6) по частям с учетом предельных условий (15.4) получаем:
- •Обобщим полученные результаты для функционала
- •§ 16. Принципы наименьшего действия Гамильтона-Остроградського.
- •§ 17. Канонические уравнения движения.
- •Подставляя (17.8) в (17.7), получаем
- •§ 18. Скобоки Пуассона.
- •§ 19. Уравнение Гамильтона-Якоби.
§ 10. Закон сохранения импульса и его связь с однородностью пространства.
Рассмотрим замкнутую механическую систему n взаимодействующих между собой материальных точек.
В
силу однородности
пространства
уравнения движения (9.5) должны быть
инвариантны
(неизменны) при любом параллельном
переносе
замкнутой системы как одного целого в
пространстве.
Ясно, что при этом не должно быть и
никакого изменения потенциальной
энергии системы
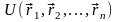 ,
существенно определяющей форму уравнений
(9.5). Эта инвариантность U накладывает
сильные ограничения на ее явный вид:
может быть только функцией взаимных
положений точек системы, т.е. функцией
переменных вида
,
существенно определяющей форму уравнений
(9.5). Эта инвариантность U накладывает
сильные ограничения на ее явный вид:
может быть только функцией взаимных
положений точек системы, т.е. функцией
переменных вида
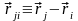 .
.
Математически
параллельный перенос (сдвиг) системы в
просторные на произвольный бесконечно
малый вектор
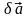 записывается
в виде
записывается
в виде
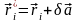 ,
.
(10.1)
,
.
(10.1)
Изменение U при этом преобразовании координат формально можно записать следующим образом:
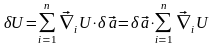 .
(10.2)
.
(10.2)
Однако,
так как никакого изменения U на самом
деле не происходит, то
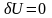 ;
поэтому учитывая, что
;
поэтому учитывая, что
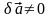 ,
с учетом (10.2) получаем для замкнутой
системы
,
с учетом (10.2) получаем для замкнутой
системы
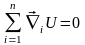 .
(10.3)
.
(10.3)
Далее, записывая уравнения движения (9.5) в виде
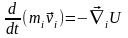 ,
.
(10.4)
,
.
(10.4)
и суммируя их почленно, имеем уравнение
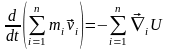 .
(10.5)
.
(10.5)
С помощью (10.5) перепишем условие (10.3) в следующем окончательном виде
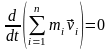 .
(10.6)
.
(10.6)
Уравнение (10.6) показывает, что в процессе движения замкнутой системы сохраняется его импульс (см. § 3)
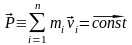 .
(10.7)
.
(10.7)
Так как (10.7) – векторное равенство, эквивалентное трем скалярным
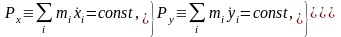 (10.8)
(10.8)
то можно сказать, что с однородностью пространства связаны три первых интеграла движения замкнутой механической системы. Аддитивность вектора импульса системы очевидна из его определения; важно отметить, что в отличие от энергии импульс системы равен сумме импульсов
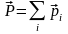 ;
;
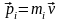 (10.9)
(10.9)
отдельных материальных точек независимо от того, можно или нельзя пренебрегать их взаимодействием между собой.
Т.о., закон сохранения импульса можно сформулировать так: следствием однородности пространства является сохранение импульса замкнутой механической системы.
Замечание 1. Закон сохранения механического импульса (10.7) является частным случаем всеобщего закона сохранения и превращения импульса различных форм движения материи. Следовательно, всякий раз, когда мы сталкиваемся с не сохранением импульса замкнутой механической системы, то причину исчезновения механического импульса следует искать в превращении некоторой его части в импульс других форм или видов движения материи (или в ошибочности нашего предположения о замкнутости системы в более широком, физическом смысле).
Замечание
2. Не
сохранение импульса
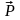 у незамкнутой
системы не исключает возможность
сохранения отдельных составляющих
импульса. Более того, из изложенного
ясно видно, что если внешнее
силовое поле обладает трансляционной
симметрией вдоль некоторого направления
у незамкнутой
системы не исключает возможность
сохранения отдельных составляющих
импульса. Более того, из изложенного
ясно видно, что если внешнее
силовое поле обладает трансляционной
симметрией вдоль некоторого направления
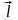 в пространстве, то потенциальная энергия
системы не изменяется при параллельном
переносе этой системы как целого вдоль
(т.е.
в пространстве, то потенциальная энергия
системы не изменяется при параллельном
переносе этой системы как целого вдоль
(т.е.
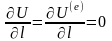 ),
поэтому у такой системы сохраняется
проекция вектора импульса на указанное
направление (т.е.
),
поэтому у такой системы сохраняется
проекция вектора импульса на указанное
направление (т.е.
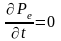 или
или
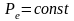 ).
).
