
- •Часть I (модуль 1)
- •Лекция 1 Введение
- •Модуль 1
- •Методы исследования вычислительных систем
- •§1.1 Классификация вс по назначению, по возможностям ос и методы исследования вс
- •Классификация вс по возможностям ос
- •Классификация вс по назначению
- •§1.2. Сущность аналитических методов исследования вс. Системы массового обслуживания (смо) и вычислительные системы.
- •§1.3. Модель процессора и оперативной памяти на основе смо
- •Лекция 3
- •§1.4. Модели каналов на основе смо, обслуживающих внешние устройства
- •§1.5. Стохастическая сетевая модель. Граф передач и матрица вероятностей передач. Экспоненциальная стохастическая сетевая модель
- •§1.6. Разомкнутые и замкнутые стохастические сети. Параметры стохастических сетей
- •Лекция 4
- •§1.7. Расчет интенсивностей потоков в стохастических сетях
- •§1.8. Характеристики стохастических сетей
- •§1.9. Структура многопроцессорной вс с общей памятью и ее характеристики
- •§1.10. Структура многопроцессорной вс с индивидуальной памятью и её характеристики
- •Лекция 11
- •§1.11. Достоинства и недостатки аналитических методов исследования вс Достоинства:
- •Недостатки:
- •Лекция 5
- •§1.12. Сущность использования имитационного моделирования для исследования вычислительных систем
- •§1.13. Общие сведения о системе программного обеспечения gpss pc.
- •§1.14. Физическое, модельное, машинное время
- •Лекция 6
- •§1.15. Пример структуры вычислительной системы для имитационного моделирования
- •Лекция 7
- •§1.16. Пример построения имитационной модели каналов передачи данных.
§1.3. Модель процессора и оперативной памяти на основе смо
Модель “процессор-оперативная-память” можно рассматривать как отображение следующего устройства.
На рис. 1.2. представлена упрощенная структура модели процессора (Пр) и оперативной памяти (ОП). Предполагается, что объём ОП достаточен для хранения прикладных программ (задачи) и обращение процессора к памяти не приводит к дополнительным задержкам. В связи с указанным объем оперативной памяти и задержки обращения к ОП не учитываются.
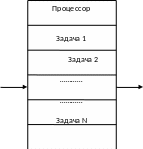
Рис. 1.2.
Тогда модель одного процессора с оперативной памятью можно представить, как показано на рис. 1.3, в виде одноканальной СМО. Группа однотипных процессоров, функционирующих с ОП, представляется, как показано на рис. 1.4. в виде многоканальной СМО.
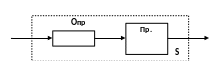
Рис. 1.3.

Рис. 1.4.
Лекция 3
§1.4. Модели каналов на основе смо, обслуживающих внешние устройства

Рис. 1.4.
Каналы будем подразделять на две группы:
- обслуживающие медленнодействующие внешние устройства (ВУ) или мультиплексные каналы (принтер);
- обслуживающие быстродействующие устройства или селекторные каналы.
1. Особенностью мультиплексных каналов (МК) является то, что основные задержки в работе вносятся самими внешними устройствами (ВУ), а задержки собственно канала по сравнению с заданными ВУ малы (в модели ими можно пренебречь). При этом обслуживание обычно осуществляется по кольцу в соответствии с последовательно выделяемыми квантами времени для каждого устройства.
В этой модели собственно нет канала, так как задержки, вносимые им столь малы, что мы им пренебрегли. Поэтому здесь всё зависит от ВУ. Пример представления модели мультиплексного канала на основе СМО представлен на рис. 1.5.
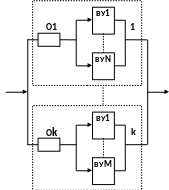
Рис. 1.5.
2. Особенностью селекторных каналов является то, что каналы используются монопольно для обслуживания отдельных устройств процессором передачи данных (ПД).
В работе каналов выделяются два этапа:
подготовительный; Например, подвод зоны диска; подвод адреса ленты.
передача информации по каналу связи со считыванием или записью.
На
рис. 1.6
представлена
модель селекторного канала для разнотипных
внешних устройств (n+1
- средняя задержка передачи данных;
 -
средние задержки в установившемся
режиме (одноканальные СМО).
-
средние задержки в установившемся
режиме (одноканальные СМО).
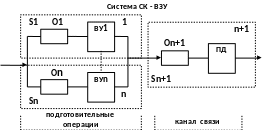
Рис. 1.6
На рис. 1.7. представлена модель селекторного канала для однотипных внешних устройств (задержка у всех ВУ одинаковая (многоканальная СМО).

Рис. 1.7
§1.5. Стохастическая сетевая модель. Граф передач и матрица вероятностей передач. Экспоненциальная стохастическая сетевая модель
Модель вычислительной системы может быть представлена как совокупность рассмотренных СМО, которые отображают отдельные устройства или группы однотипных устройств, а также связи между устройствами. Совокупность взаимосвязанных СМО называется стохастической сетевой моделью.
В конфигурации стохастической сети отражаются:
а) структура вычислительной системы;
б) последовательность выполняемых вычислительных этапов обработки информации.
Для простейших сетей в теории массового обслуживания принято:
а) входной поток является простейшим;
б) длительность обслуживания подчиняется экспоненциальному закону:
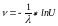 ,
,
где U – поток равномерно распределенных случайных величин. Такие стохастические сети (модели) называются экспоненциальными. На основе конфигурации экспоненциальной стохастической модели формируются аналитические выражения, по которым непосредственно могут быть оценены характеристики системы.
В качестве примера рассмотрим следующую вычислительную систему (рис.1.8), в которую входят следующие подсистемы: S1 - процессор; S2 – быстродействующее ВУ (например, накопитель на магнитных дисках (НМД)); S3 – быстродействующее ВУ (например, накопитель на магнитных лентах (НМЛ)); S4 - группа однотипных медленно действующих ВУ(например, принтеры); S5 - канал передачи данных.
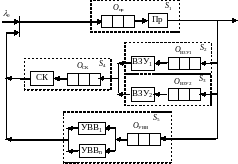
Рис. 1.8
В такой стохастической сети предполагается, что отсутствует последействие. Это означает, что все последующие события могут зависеть только от текущего события и не зависят от предшествующих событий. Такой процесс называется марковским. Он характеризуется множеством состояний S1 . . . S5 и матрицей вероятностей перехода в эти состояния. Вычислительный процесс всегда начинается с момента поступления заявки в процессор (состояние S1). Инициализация обращения к любому из устройств осуществляется только процессором. Связи между отдельными СМО устанавливаются в результате анализа порядка следования этапов обработки заявок. Для отображения вычислительного процесса используется направленный граф передач. Вершины графа соответствуют состояниям вычислительного процесса S1 , S2, … Sn, а дуги между вершинами указывают на связи между отдельными СМО (переход системы из одного состояния в другое). Дуги взвешиваются вероятностями перехода. Если система может перейти из одного состояния в одно из нескольких состояний, то возникает необходимость оценки вероятностей переходов. При этом строится матрица вероятностей передач.
Этап – процесс, завершающийся выходом заявки из процессора.
П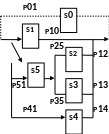 усть
имеем систему, модель которой в укрупненном
представлении имеет вид, представленный
на рис.1.9, где:
S1
–процессор; S2,
S3
–
быстродействующие
устройства; S4
– медленнодействующее устройство
(например, принтер); S5
– селекторный
канал; S0
– источник запросов.
усть
имеем систему, модель которой в укрупненном
представлении имеет вид, представленный
на рис.1.9, где:
S1
–процессор; S2,
S3
–
быстродействующие
устройства; S4
– медленнодействующее устройство
(например, принтер); S5
– селекторный
канал; S0
– источник запросов.
Рис. 1.9
Граф вероятностей передач и матрица вероятностей передач представлены на рис. 1.10.
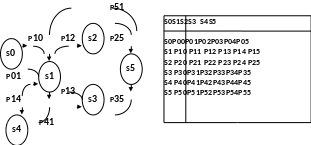
Рис. 1.10
Здесь указаны вероятности перехода pji из j -ой подсистемы в i-ю. S0 - источник заявок (генератор заявок) в системе. Таким образам, число подсистем в системе (n+1), и размерность матрицы вероятностей передач соответственно тоже (n+1).
Рассмотрим, как оценивается вероятность перехода pji из j -ой подсистемы в i -ю. Для этого возьмём две вершины графа Sj и Si (рис.1.11) и тогда pji можно определить в виде
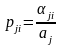 ,
,
где
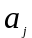 - весь
суммарный (средний) поток, который
исходит из подсистемы
Sj;
- весь
суммарный (средний) поток, который
исходит из подсистемы
Sj;
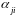 -
средний поток заявок, который из
подсистемы Sj
поступает в Si;
входной и выходной потоки равны.
-
средний поток заявок, который из
подсистемы Sj
поступает в Si;
входной и выходной потоки равны.
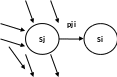 i
i
Рис.1.11
Рассмотрим простейший пример расчета для системы на рис.1.9. Пусть S2 и S3 - внешние накопители. Имеется N файлов, которые распределены между накопителями S2 и S3. К каждому файлу при решении средней задачи должно быть осуществлено Dj обращений (j = 1, N). При каждом полном решении задачи на выходе системы появляется обслуженный запрос, который направляется к S0. Пусть также к внешнему устройству S4 при обслуживании средней задачи осуществляется d обращений.
Общее количество обращений к файлам D определяется в виде
D
=
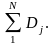
На выходе S1 заявка появляется (D + d + 1) раз.
Матрица вероятностей передач имеет вид, представленный на рис. 1.12.
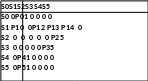
Рис.1.12.
Значения вероятностей передач определяются в следующем виде:
P01 = 1; P25 = 1; P35 = 1; P51 = 1; P41 = 1;
P10
=
 ;
P14
=
;
P14
=
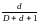 ;
P12
=
;
P12
=
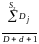 ;
P13
=
;
P13
=
 .
.
Суммы вероятностей передач по строкам должны удовлетворять соотношению
P10 + P12+P13+P14 =1.
