
- •1. Дерево решений
- •Задачи с решениями
- •3.3. Задачи для самостоятельного решения
- •Раздел 2 Теория очередей
- •5.1. Задачи с решениями
- •3. Результаты расчетов сводятся в таблицу 2.
- •Задачи для самостоятельного решения
- •Раздел 3 Управление запасами и техника управления «точно вовремя»
- •9.1. Задачи с решениями
Раздел 2 Теория очередей
Модель, иллюстрируемая одноканальной однофазной системой с пуассоновым распределением появления заявок и экспоненциальным временем обслуживания – это модель А; модель В – многоканальный эквивалент модели А; модель С характеризуется постоянным временем обслуживания; модель D – с ограниченным размером источника появления заявок.
Все четыре модели связаны с пуассоновым распределением заявок, дисциплиной обслуживания «первым пришел, первым ушел» и с однофазным сервисом.
Типичными операционными характеристиками рассматривают среднее время ожидания в очереди и в системе, среднее число заявок в очереди и в системе, время простоя и коэффициент использования системы.
Интенсивность
нагрузки систем
![]() ,
,
![]()
Величина
представляет собой долю времени
занятости канала обслуживанием требований
и изменяется в пределах
= 0 - 1. При
= 0 канал совершенно не загружен (![]() =0),
при
=1
(
=0),
при
=1
(![]() )
канал загружен полностью.
)
канал загружен полностью.
- вероятность того, что в системе есть требование, равна ;
вероятность того,
что в системе нет требований (k=0),
представляет собой вероятность
противоположного события и равна ![]() ;
;
вероятность того,
что в системе находится больше одного
требования (т.е. вероятность образования
очереди), равна
![]()
вероятность того,
что в системе более п требований, равна
![]()
— вероятность
того, что в системе находится k требований
(в очереди или в канале обслуживания),
равна
![]()
— среднее число
требований, находящихся в системе, равно
![]()
- среднее число
требований в очереди для всего периода
функционирования системы
![]() равно
равно
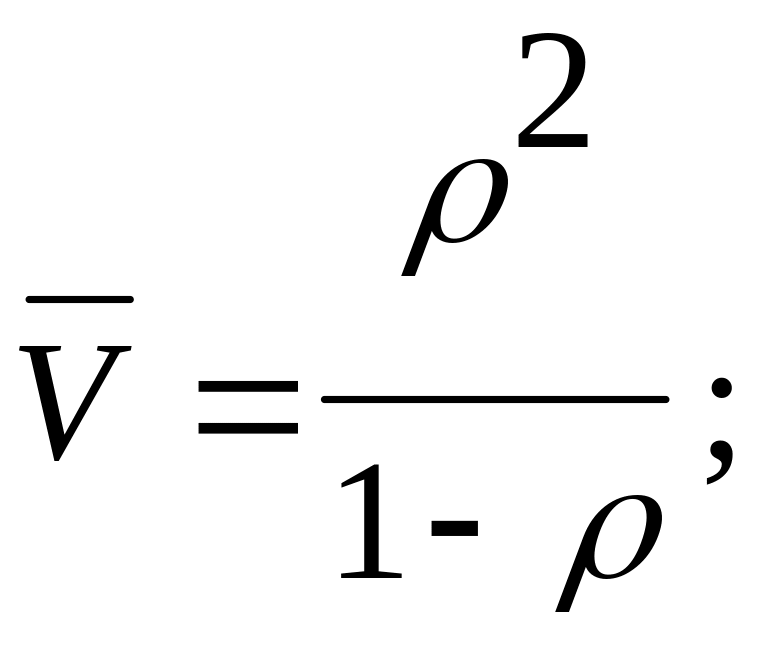
среднее число
требований в очереди для того времени,
когда очередь существует (![]() ),
равно
),
равно
![]()
— среднее время
ожидания требованием обслуживания
![]() равно
равно
![]()
среднее время
пребывания заявки в системе
![]() равно
равно
![]()
С помощью данных зависимостей можно рассчитывать основные показатели, характеризующие качество процесса обслуживания, т.е. решать задачи оценки.
Для решения задач оптимизации необходимо сформулировать критерий. Поскольку внешние условия функционирования считаются заданными характером и интенсивностью потока заявок, цель оптимизации состоит в том, чтобы выбрать такую систему обслуживания, которая позволила бы свести потери от ожидания в очереди и простоя канала обслуживания до минимума. Эта цель достигается главным образом выбором оптимальной пропускной способности канала.
Задачу можно сформулировать как обратную задачу, которая состоит в выборе лучшей пропускной способности канала обслуживания. Лучшей будем считать такую пропускную способность, которая при заданном потоке заявок обеспечит минимальные потери от нахождения заявок в очереди и затрат на содержание канала обслуживания.
![]()
Потери от нахождения в системе одной заявки в единицу времени С1, а затраты на содержание единицы пропускной способности канала обслуживания С2..
Для многоканальных систем обслуживания основными параметрами являются:
- среднее число
требований в очереди (![]() );
);
- среднее число
требований в системе (![]() ;
;
- среднее время
ожидания обслуживания одного требования
(![]() ;
;
- среднее время
пребывания требования в системе (![]()
- вероятность
образования очереди (вероятность того,
что в системе с S каналами находится
![]() требований).
требований).
Эти характеристики позволяют не только определять основные показатели многоканальных систем обслуживания, но и решать задачи оптимизации их пропускной способности. Для нахождения оптимального числа каналов в системе можно воспользоваться целевой функцией следующего вида:
![]()
где L - потери от ожидания требованиями обслуживания и от простоев каналов обслуживания в единицу времени;
С![]() -
убытки от ожидания одной заявкой
обслуживания в единицу времени;
-
убытки от ожидания одной заявкой
обслуживания в единицу времени;
- среднее число заявок, ожидающих обслуживания;
С![]() -
убытки от простоя канала обслуживания
в единицу времени;
-
убытки от простоя канала обслуживания
в единицу времени;
![]() - среднее число
незанятых каналов.
- среднее число
незанятых каналов.
