Проектирование логического комбинационного автомата

Проектирование логического управляющего автомата выполняется методами логического синтеза. Под синтезом понимается процесс составления логических выражений, описывающих схему устройства по заданным условиям технологического процесса. Процедуру синтеза можно разделить на следующие этапы:

• Получение логической функции, описывающей алгоритм функционирования проектируемого устройства;

• Минимизация логической функции.

• Проверка минимизации.

• Построение комбинационной логической схемы.

• Проверка работы схемы.

Получение логической функции

Рассмотрим решение задачи синтеза на примере таблицы истинности, приведенной в табл. 3.

Таблица 3 Таблица истинности (контрольный вариант)

Номер набора	Аргументы (входные переменные)				Выходная переменная Y=F(Х3,Х2,Х1,Х0)
	Х3	Х2	Х1	Х0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1	0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1	0 0 1 0 0 0 0 0 1 1 0 0 1 1 1 0

Запись логической функции, описывающей работу схемы, обычно производят в виде дизъюнктивной нормальной формы (ДНФ). ДНФ - это дизъюнкция (логических сумм) конъюнкций (логических произведений) аргументов или их инверсий. Для каждой функции существует несколько эквивалентных ДНФ.

В классе ДНФ в качестве исходной формы выделяют совершенную дизъюнктивную нормальную форму (СДНФ). Для каждой функции существует только одна СДНФ.

СДНФ удобно находить в такой последовательности:

а) выбрать в таблице истинности (табл. 3) все наборы (второй, восьмой, девятый, двенадцатый, тринадцатый и четырнадцатый - всего шесть наборов) значе­ний аргументов Х₃, Х₂ , Х₁, Х₀ на которых функция Y=F(Х₃,Х₂,Х₁,Х₀) обращается в еди­ницу;

б) выписать ряд конъюнкций всех аргументов и соединить их знаками дизъюнкций. Количество конъюнкций должно равняться числу наборов, на которых функция обраща­ется в единицу

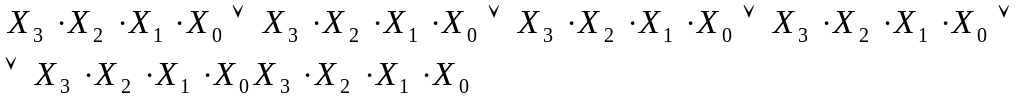
(6)

в) каждое произведение привести в соответствие с одним из выбранных наборов, и над аргументами, равными нулю, поставить знаки инверсии (отрицания). Каждое произведение называется исходной конъюнкцией (минтермом, конституентом единицы).

Полученная форма является развернутой СДНФ логической функции:

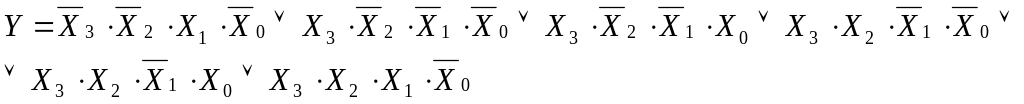
(7)

Таким образом, СДНФ логической функции записывается в виде дизъюнкции минтермов, каждый из которых является конъюнкцией, включающей все аргументы функции (в прямом или инверсном виде) и обращающимся в единицу на одном и только одном наборе значений аргументов.

Сокращенная запись СДНФ логической функции имеет вид:

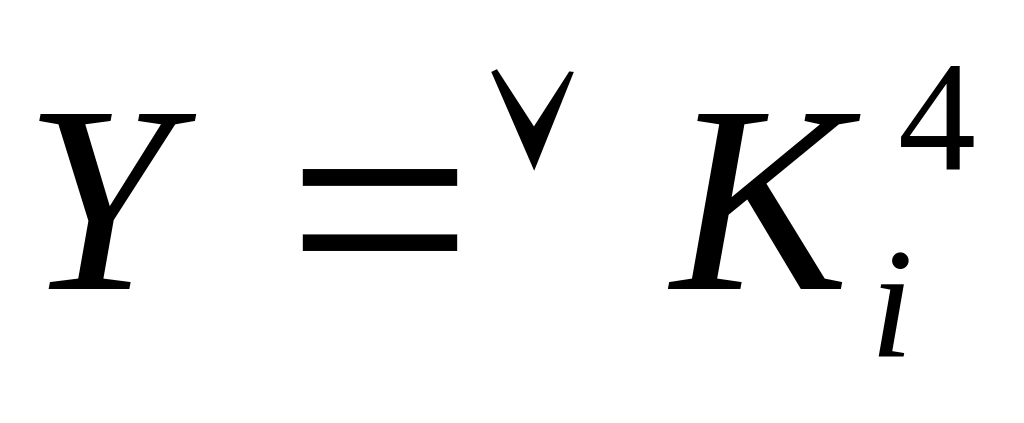, при i = 2, 8, 9, 12, 13, 14.

(8)

Выражение (8) читается следующим образом: «дизъюнкция конъюнкций четвертого ранга, принимающая единичные значения на наборах 2, 8, 9, 12, 13, 14». Рангом наз. длина функции, равная количеству аргументов.