12. Самоторможение в червячной передаче.

М1- момент на валу червяка,М2 — момент нагрузки на валу колеса.

Движение зуба колеса по витку червяка это перемещение по наклонной плоскости, расположенной под углом γ к горизонтали. Сила F2 момент нагрузки М2 и диаметр d2 известны.При отсутствии движения сила F2 уравновешивается силой F'1 = F2tgγ . При движении возникает сила трения FТР, отклоняющая проекцию Fn на угол трения ρ.

F2= F1 /tg (γ-ρ)

Следовательно, при γ=ρ передача невозможна. Это условие отсутствияпередачи называется самоторможением. т. е. Движение возможно при γ > ρ.

Это обеспечивает плавность хода, бесшумность, возможность исключения обратной передачи вращения, низкий КПД из-за больших потерь на трение в зацеплении

13. Планетарные механизмы: состав, назначение, основные характеристики, достоинства и недостатки.

Передачи, имеющие зубчатые или фрикционные колеса с перемещающимися осям, называют планетарными. Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение, называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси.

Наиболее распространена зубчатая однорядная планетарная передача (рис.60). Она состоит из центрального колеса 1 с наружными зубьями, неподвижного (центрального) колеса 2 с внутренними зубьями и водила на котором закреплены оси планетарных колес g (или сателлитов).

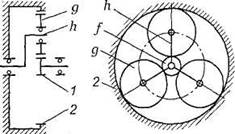
Рис.60. Планетарная передача

 

Водило вместе с сателлитами вращается вокруг центральной оси, а са­теллиты обкатываются по центральным колесам и вращаются вокруг своих осей, совершая движения, подобные движению планет. При неподвижном колесе 2 движение передается от колеса 1 к водилу h или наоборот.

Планетарную передачу ус­пешно применяют в транспортном машиностроении, станкостроении, приборостроении.

Достоинства и недостатки планетарных передач.

Основное достоинство — широкие кинематические возможности, по­зволяющие использовать передачу в качестве редуктора коробки скоро­стей, передаточное число в которой изменяется путем поочередного тормо­жения различных звеньев, и как дифференциальный механизм.

- Планетарный принцип позволяет получать большие передаточные чис­ла (до тысячи и больше) без применения многоступенчатых передач.

- Эти передачи компактные и имеют малую массу. Переход от простых передач к планетарным позволяет во многих случаях снизить их массу в 4 раза и более.

- Сателлиты в планетарной передаче расположены симметрично, а это снижает нагрузки на опоры (силы в передаче взаимно уравновешиваются), что приводит к снижению потерь и упрощает конструкцию опор.

- Эти передачи работают с меньшим шумом, чем обычные зубчатые и имеют более лёгкое управление и регулирование скорости;

- Имеют малый шум вследствие замыкания сил в механизме.

Основные недостатки: повышенные требования к точности изготовле­ния и монтажа (для обеспечения сборки планетарных передач необходимо соблюдать условие соосности (совпадение геометрических центров колёс); условие сборки (сумма зубьев центральных колёс кратна числу сателлитов) и соседства (вершины зубьев сателлитов не соприкасаются друг с другом); резкое снижение КПД передачи с увеличением передаточ­ного отношения.

Характеристики: 1)Число сателитов k. 2).Соосность входного и выходного вала. 3).Равенство углов между сателитами. 3).Условие соседства при k>3.

Передаточное отношение.

Для определения передаточного отношения планетарной передачи ис­пользуется метод Виллиса — метод останова водила.

Передаточное отношение планетарной передачи (см. рис. 60)

(33)

где и — угловые скорости колес 1 и 2 относительно води­ла h; и — числа зубьев этих колес.

Для реальной планетарной передачи (колесо 2 закреплено неподвиж­но, колесо 1 — ведущее, водило h ведомое) при из формулы (36) получим

или

(34)

Для однорядной планетарной передачи , для многоступен­чатых , для кинематических передач . Чем больше передаточное отношение планетарной передачи, тем меньше КПД (0,99...0,1).

Расчет на контактную прочность зубьев планетарных передач проводится по аналогии с расчетом обыкновенных зубчатых передач от­дельно для каждого зацепления (см. рис.60): пара колес 1—g (внешнее зацепление) и g—2 — (внутреннее). Для таких передач достаточно рассчи­тать только внешнее зацепление, так как модули и силы в зацеплениях одинаковые, а внутреннее зацепление прочнее внешнего.

Проектировочный расчет планетарной передачи на контактную ус­талость активных поверхностей зубьев проводится по следующей формуле:

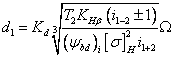(35)

где d₁ — делительный диаметр ведущего звена (шестерни), мм; K_d = 78 МПа — вспомогательный коэффициент (рассматриваются сталь­ные прямозубые колеса); T₂ — вращающий момент на шестерне, Нмм; — коэффициент нагрузки (см. табл.4); — коэффици­ент, учитывающий неравномерность распределения нагрузки среди сател­литов; — передаточное отношение; — коэффициент длины зуба (ширины колеса); — допускаемое контактное напряжение, МПа.

При расчете планетарных передач выбор числа зубьев колес зависит не только от передаточного отношения , но и от условий собираемости пере­дач. При этом сумма зубьев центральных колес должна быть кратной числу сателлитов (лучше 3).