Частота затухающих колебаний

. (3.22)

Период затухающих колебаний Т* представляет собой промежуток времени между двумя последовательными прохождениями точки в одном направлении через положение покоя (рис. 3.6):

. (3.23)

Формулу (24) можно представить в следующем виде:

, (3.24)

где Т = 2π/k — период свободных колебаний этой же точки.

Формула (3.24) показывает, что период затухающих колебаний больше периода свободных колебаний точки. Однако при небольшом сопротивлении это увеличение незначительно. В случае небольшого сопротивления период затухающих колебаний можно принимать рав­ным периоду свободных колебаний.

Амплитудой затухающих колебаний называют наибольшие отклонения точки в ту и другую сторону от положения покоя в течение каждого колебания.

Из последовательных значений переменной амплитуды можно составить ряд (рис. 3.7): .

Определим отношение последовательных членов ряда A_i+1 и A_i, соответствующих моментам времени :

. (3.25)

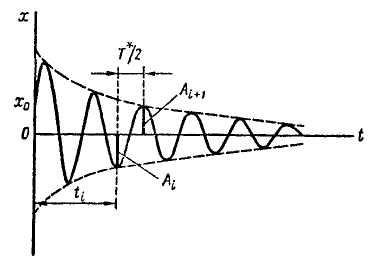
Рис. 3.7

Так как отношение А_i+1 /А_i постоянно и по величине меньше единицы, то последовательные значения амплитуды составляют убывающую геометрическую прогрессию со знаменателем .

Отвлеченное число называется декрементом колебаний: натуральный логарифм декремента, т. е. величина , называется логарифмическим декрементом:

. (3.26)

Коэффициент n называют коэффициентом затухания. Затухание колебаний происходит очень быстро даже при малом сопротивлении. Так, например, при n=0,05k

,

т.е. период затухающих колебаний Т* отличается от периода свободных колебаний Т лишь на 0,125%, а амплитуда колебаний за время одного полного колебания уменьшается на 0,27 своей величины, а после 10 полных колебаний становится равной лишь 0,04304 своего первоначального значения.

Tаким образом, основное влияние сопротивления на свободные колебания материальной точки выражается в уменьшении амплитуды колебаний с течением времени, т. е. в затухании колебаний.

Случаи апериодического движения. Движение материальной точки теряет колебательный характер и становится апериодическим в случае большого сопротивления, т. е. при n≥ k или α ≥ 2 .

а) При n > k корни общее решение уравнения (3.15) имеет вид

. (3.27)

Введем вместо постоянных интегрирования C₁ и С₂ две новые постоянные В₁ и В₂, положив

.

Подставим эти значения C₁ и С₂ в уравнение (3.27):

.

Введем в полученное уравнение гиперболические функции

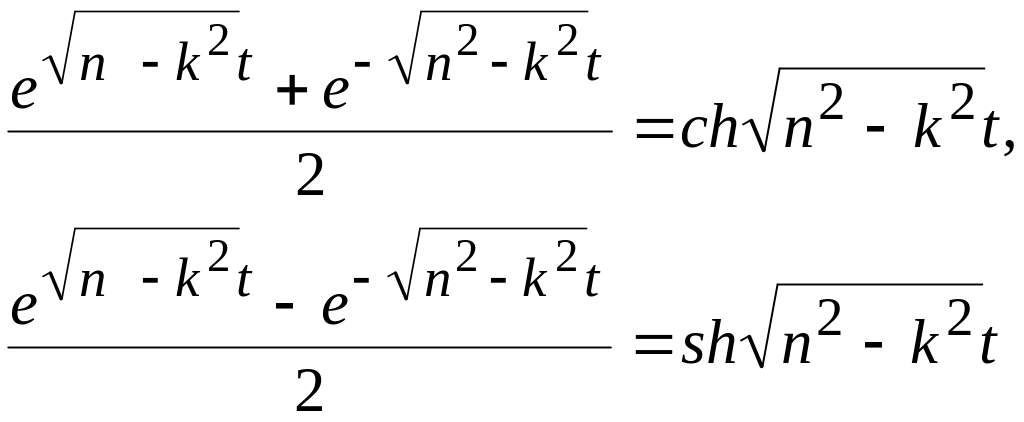
Тогда получаем уравнение в следующем виде:

.

Дальнейшее преобразование этого уравнения проведем, заменив постоянные B₁ и В₂ двумя другими постоянными A и β по условию

.

Тогда уравнение примет вид

. (3.28)

Уравнение движения точки (3.28) показывает, что рассматриваемое движение точки не является колебательным, так как гиперболический синус не является периодической функцией. В зависимости от начальных условий материальная точка может совершать одно из движений, графики которых показаны на рис. 3.8—3.10. Эти графики соответствуют начальному отклонению точки от положения покоя на величину .

На рис. 3.8 показан график движения точки с начальной скоростью v₀, имеющей направление, совпадающее с направлением оси x. Благодаря этой скорости точка сначала удаляется от положения покоя, а затем под действием восстанавливающей силы постепенно приближается к этому положению.

Графики (рис. 3.9 и 3.10) соответствуют движению точки с начальной скоростью , направленной противоположно направлению оси х. При достаточно большой начальной скорости точка может совершить один переход через положение покоя и затем при обратном движении приближаться к этому положению (рис. 3.9).

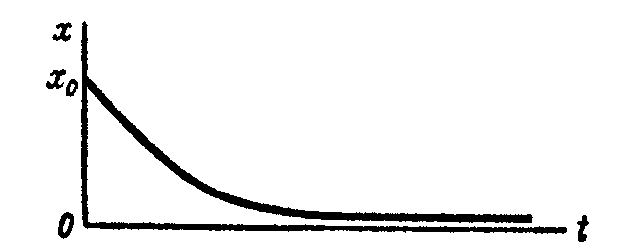
Рис. 3.8 Рис. 3.9 Рис. 3.10

б) При n=k общее решение уравнения (3.15) в этом случае имеет вид

. (3.29)

Чтобы найти C₁ и С₂, получим уравнение, определяющее скорость точки, продифференцировав уравнение (3.29):

. (3.30)

Пусть в начальный момент t= 0 точка имеет координаты x₀ и проекцию скорости на ось х, равную .

Подставим в уравнения (3.29) и (3.30) эти начальные условия:

,

откуда

.

Зная значения С₁ и С₂, представим уравнение (3.29) в следующем виде:

. (3.31)

Движение точки, определяемое уравнением (3.31), является также апериодическим.

Пример. Тело весом G = 20 Н, лежащее на гладкой горизонтальной плоскости и прикрепленное к концу недеформированной пружины (рис. 3.11), отклоняют из положения покоя вправо, растягивая пружину на 4 см, и отпускают, сообщая начальную скорость 56 см/с, направленную влево (удлинение пружины на 1 см вызывается силой 4 Н). Определить дальнейшее движение тела, пренебрегая массой пружины.

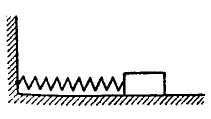
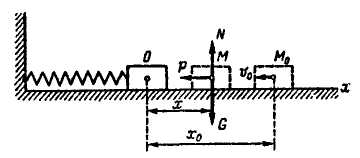
Рис. 11 Рис. 12

Решение. Направим ось х горизонтально вправо, считая началом координат О положение покоя тела, принятого за материальную точку. Тогда начальные условия будут следующими (рис. 3.12):

.

В произвольный момент времени t на тело М, имеющее координату х, действуют сила тяжести , реакция плоскости и сила упругости деформированной пружины , направленная к точке О. Модуль силы пропорционален деформации пружины, т. е.

,

где с - коэффициент жесткости пружины.

Проекция силы на ось х

.

По условию задачи, с = 4 Н/см.

Дифференциальное уравнение свободных колебаний:

.

Решение дифференциального уравнения представим в форме:

.

Вычислим частоту и период колебаний по формулам:

;

.

Амплитуду А и начальную фазу β свободных колебаний тела вычислим по начальным условиям с помощью формул:

;

.

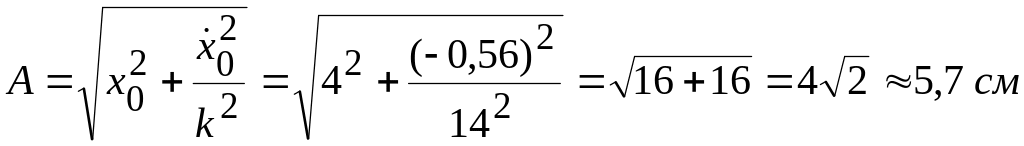Уравнение свободных колебаний груза имеет вид

.

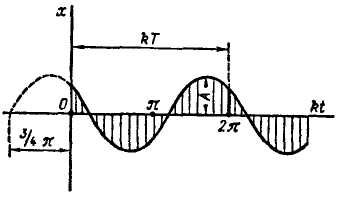
Рис. 3.13

На рис. 3.13 построен график движения, соответствующего полученному уравнению. При этом по оси абсцисс отложены не значения t, а пропорциональные им произведения kt. Тогда начальная фаза β изображается величиной смещения начала волны синусоиды в направлении, противоположном направлению оси абсцисс.

Примечание. Амплитуда свободных колебаний зависит как от начального отклонения тела из положения покоя, так и от начальной скорости. При этом направление начальной скорости не влияет на амплитуду. Так, если начальную скорость направить вправо ( =56 см/с), амплитуда будет иметь ту же величину. Если тело опустить без начальной скорости ( = 0), то амплитуда

,

т. е. амплитуда будет равна начальному отклонению тела от положения покоя. Наличие начальной скорости увеличивает амплитуду,

Лекция 4

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ТОЧКИ

1. Вынужденные колебания точки.

возмущающая сила

Вынужденные колебания совершает материальная точка, на которую наряду с восстанавливающей силой действует периодически изменяющаяся сила, называемая возмущающей силой.

Практически наиболее важным является случай, когда возмущающая силa изменяется по гармоническому закону, т. е. проекция ее на ось х, направленную по траектории точки, определяется так:

. (4.1)

где Н – максимальный модуль, или амплитуда, возмущающей силы; р - частота изменения возмущающей силы, равная числу полных циклов изменения возмущающей силы за 2π с; pt+δ - фаза изменения возмущающей силы: δ- начальная фаза изменения возмущающей силы.

Период изменения возмущающей силы определяется по ее частоте:

. (4.2)

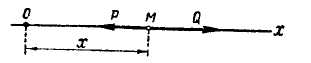
Рис. 4.1

Рассмотрим прямолинейное движение материальной точки М (рис. 4.1) под действием восстанавливающей силы и возмущающей силы , изменяющейся по гармоническому закону.

Направим ось х по прямолинейной траектории точки М, а начало координат поместим в положение покоя точки М, соответствующее недеформированной пружине.

Составим дифференциальное уравнение движения точки, учитывая, что на точку М с координатой х в момент времени t действуют силы и , имеющие проекции на ось х:

и .

Тогда

,

или

.

Здесь - квадрат частоты свободных колебаний. Введем обозначение Н/т = h:

. (4.3)

Уравнение (4.3) представляет собой дифференциальное уравнение вынужденных колебаний материальной точки.

Общее решение уравнения (4.3) складывается из общего решения однородною уравнения и частного решения данного уравнения (4.3):

.

Однородное уравнение имеет общее решение:

.

В соответствии с видом функции f(t) в правой части уравнения (4.3) будем искать частное решение уравнения (4.3) в виде

. (4.4)

Определим постоянную А_B подстановкой функции (4.4) в уравнение (4.3). Так как , то после подстановки (4.4) в уравнение (4.3)

.

Полученное равенство должно быть справедливо при любом значении sin (pt +δ). Это выполняется лишь при равенстве коэффициентов в левой и правой частях, т. е.

,

откуда

. (4.5)

Подставляя значение А_В в выражение (4.4), находим искомое частное решение уравнения (4.3):

. (4.6)