5 Решение задачи при действии силы, зависящей от положения точки
Материальная
точка М
массой m=20
г
отталкивается от некоторого центр О
с силой, обратно пропорциональной кубу
расстояния ОМ.
В начальный момент расстояние ОМ=5
см,
скорость точки
.
направленная по прямой ОМ
от центра О,
и сила отталкивания Р
= 0,4 мН.
Требуется получить уравнение движение точки под действием силы отталкивания, а также определить скорость, приобретенную точкой на расстоянии 20 см от центра О (рис. 2.5).
Решение. Центр отталкивания О примем за начало координат, ось х направим но прямой, соединяющей этот центр с движущейся точкой М. Установим начальные условия:
.
На точку действует сила отталкивания , направленная по оси х. Модуль этой силы обратно пропорционален кубу расстояния ОМ:
.
Значение
коэффициента k
можно определи пo условию, что при
сила отталкивания
:
.
Составим дифференциальное уравнение движения точки М:
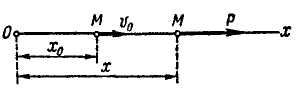
Рис. 2.5
.
Чтобы понизить порядок дифференциального уравнения, представим ускорение в виде
.
где v - алгебраическое значение скорости. Тогда
.
Последнее уравнение содержит переменную величину х, кроме переменных v и t. Исключаем из уравнения переменную t, применив преобразование:
.
(2.6)
Дифференциальное уравнение движения точки примет вид
.
Разделим переменные
.
При
интегрировании уравнения воспользуемся
определенными интегралами с переменным
верхним пределом. При изменении скорости
от
до v
координата точки изменяется от
до х.
Тогда
,
или
,
откуда
.
Подставим сюда числовые значения k, т, :
,
или
.
(2.7)
Полученное выражение определяет скорость v точки в зависимости от ее координаты х. Из этого уравнения можно найти искомое значение скорости при х= 20 см:
.
Чтобы получить уравнение движения точки x =f(t), воспользуемся уравнением (2.7).
или
Разделим переменные:
.
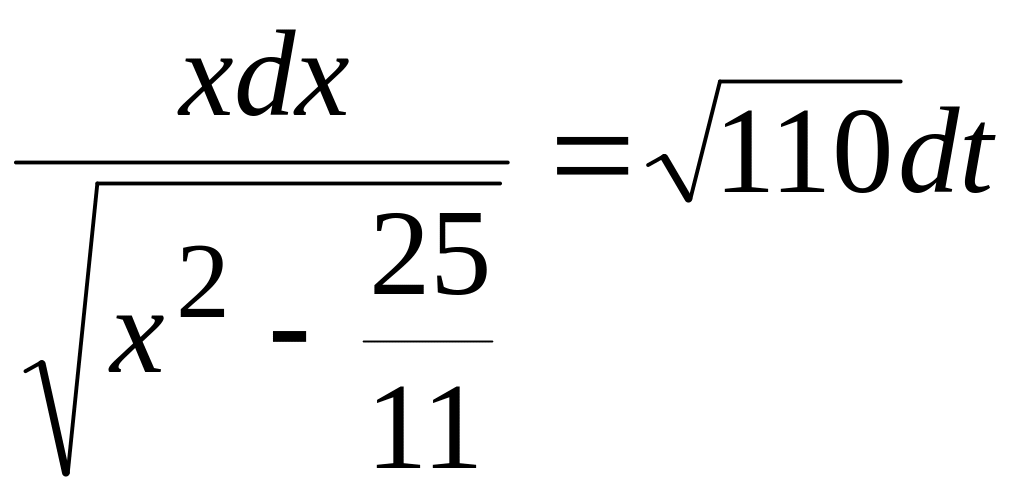Левую
часть проинтегрируем в пределах от
до х,
а правую - в пределах от
до t:
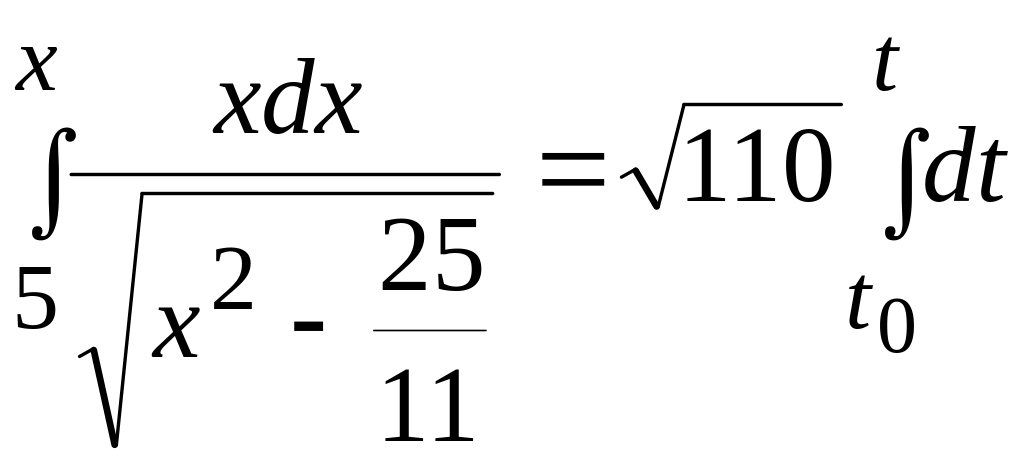или
.
Подставим сюда значения пределов:
или
.
Возведем в квадрат обе части уравнения:
.
Отсюда получим уравнение движения точки:
см.
Примечание 1. Определенные интегралы с переменными верхними и нижними пределами, соответствующими начальными значениями переменных интегрирования, могли быть использованы и при решении предыдущих примеров. Применение их освобождает от определения постоянных интегрирования по начальным условиям. Наоборот, при решении последнего примера можно было бы применять неопределенные интегралы, определяя постоянные интегрирования по начальным условиям.
2. Преобразование (2.7) иногда удобно применять и в случае силы, зависящей от скорости. Тогда дифференциальное уравнение с переменными v и t переходит в уравнение с переменными v и х.