Задача 5. Исследование механической системы с применением уравнений Лагранжа второго рода

По условию задачи № 3 определить ускорение тела 1, используя уравнение Лагранжа П рода.

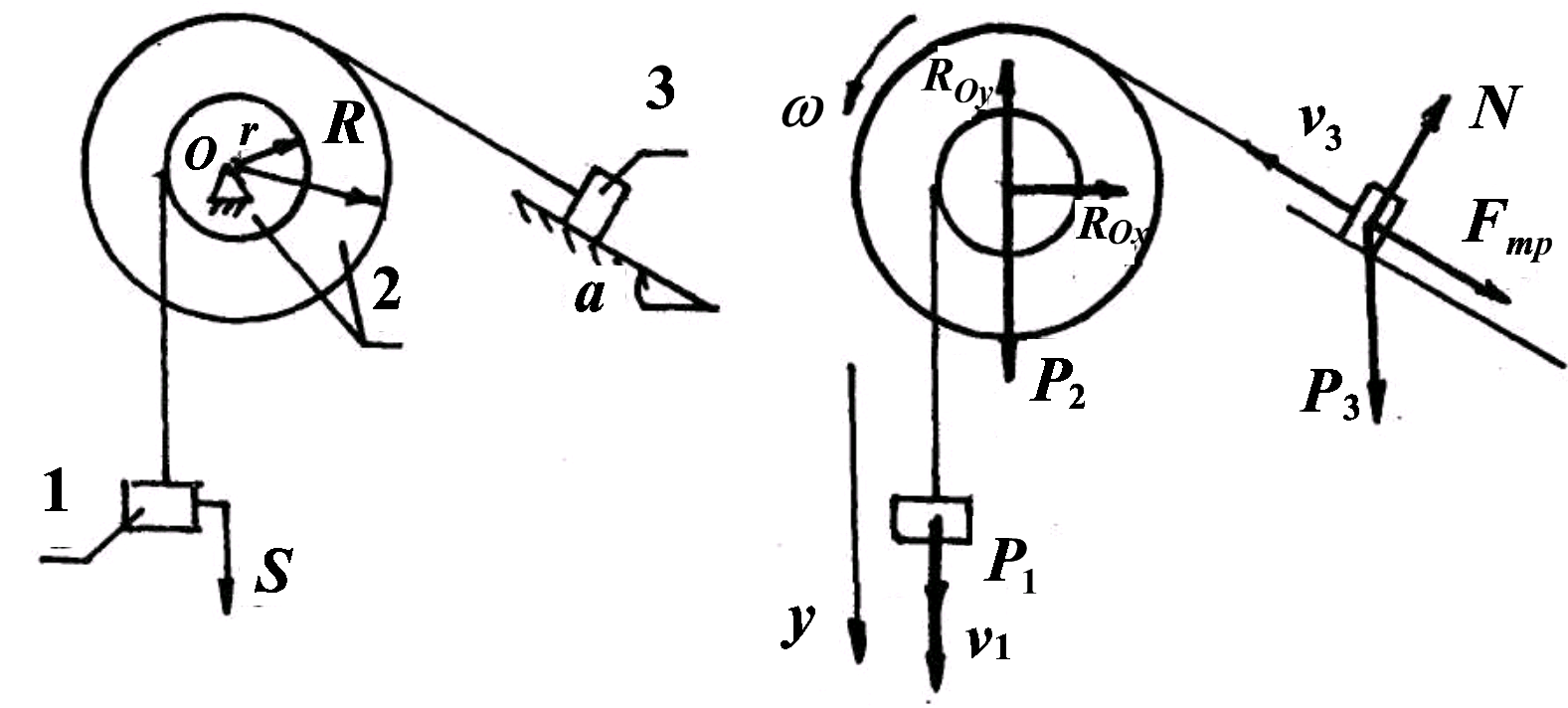
Решение.

1. Составление расчетной схемы.. На механическую систему действуют активные силы , , .

Применяя принцип освобождаемости от связей только к внешним связям, покажем на расчетной схеме реакции шарнирно-неподвижной опоры и реакции шероховатой поверхности и . Силу трения направим в сторону, противоположную движению тела 3.

Изобразим скорости тел системы исходя из того, что тело 1 опускается.

2. Выбор теоремы.

Задачу решаем, используя дифференциальное уравнение механической системы в обобщенных координатах

.

Так как система имеет одну степень свободы, а определяем ускорение тела 1, то за обобщенную координату примем координату первого тела у

q=y.

Обобщенная скорость, в таком случае, .

3. Составление уравнения.

а) Определение кинетической энергии системы.

Кинетическая энергия системы представляет собой сумму кинетических энергий тел 1,2 и 3.

.

Вычислим Q для неконсервативных сил

,

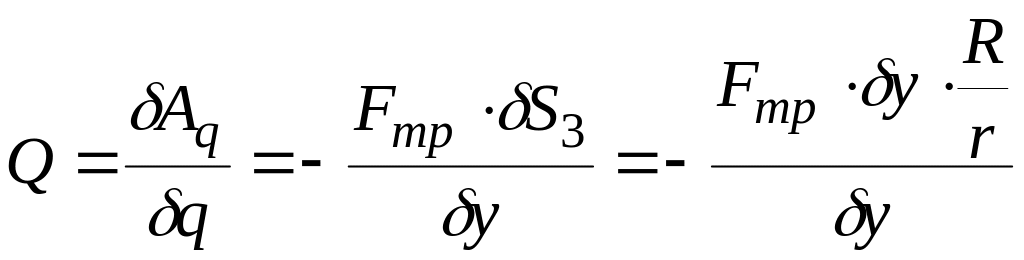то есть

.

Работа сил и на заданном приращении обобщенной координаты равна нулю, так как силы приложены к неподвижной точке. Работа нормальной реакции поверхности N также равна нулю, сила перпендикулярна направлению движения.

Подставим в обобщенную силу значения

.

или .

в) Определение потенциальной энергии системы.

Потенциальная энергия численно равна работе потенциальных сил, действующих на систему, которую необходимо совершить, чтобы вернуть систему из отклоненного положения в положение равновесия.

.

Высота, на которую переместится точка приложения силы , равна

.

В обобщенных координатах

.

Подставляя числовые параметры, запишем

.

Подставляем значения Т, П и Q в уравнение Лагранжа П рода и преобразовываем

,

,

,

так как Т не содержит у.

.

Таким образом, запишем

,

Значение ускорения тела получили со знаком «+». Это означает, что груз опускается ускоренно.

2. Кинетический потенциал. Циклические координаты

Предположим, что на рассматриваемую механическую систему на­ряду с силами, имеющими потенциал (консервативными силами), дев­ствуют силы, не имеющие потенциала (неконсервативные силы). При этом условии обобщенную силу Q_j удобно представить в виде сум­мы обобщенной силы , соответствующей консервативным силам и обобщенной силы , соответствующей неконсервативным силам :

.

Если на рассматриваемую систему действуют только консерватив­ные силы, то обобщенная сила определяется формулой:

.

В этом случае уравнения Лагранжа второго рода принимают следующий вид:

. (14.8)

Уравнения (14.8) можно преобразовать путем введения функции Лагранжа L=T- П, называемой кинетическим потенциалом.

Так как

.

.

Следовательно, кинетический потенциал является функцией обоб­щенных координат, обобщенных скоростей и времени:

. (14.9)

Потенциальная энергия является функцией только обобщенных координат и времени, а потому

.

Пользуясь этим условием, получим

.

Подставим эти частные производные в уравнения Лагранжа (14.8):

,

или

. (14.10)

Уравнения (14.10) называются уравнениями Лагранжа второго рода для консервативной системы.

Уравнения Лагранжа широко используют при изучении свободных колебаний механических систем во многих областях техники. При­менение уравнений Лагранжа второго рода к определению чистоты и периода свободных колебаний механической системы с одной сте­пенью свободы показано в примерах. Применение уравнений Лагранжа к изучению свободных и вы­нужденных колебаний механических систем с конечным числом сте­пеней свободы можно найти в ряде специальных курсов.