Задача 4. Применение общего уравнения динамики к изучению механической системы

Для заданной механической системы определить ускорение груза 1 и натяжение в ветви нити 1, к которой прикреплен груз. Массами нитей пренебречь. Система движется из состояния покоя. Считать, что , , , , см, , f= 0,1 (рис. 1).

Рис 1

Решение.

1. Составление расчетной схемы. На механическую систему действуют активные силы , , . Применяя принцип освобождаемости от связей к внешним связям, покажем , , N. Силу трения изобразим в сторону, противоположную предполагаемую направлению движения.

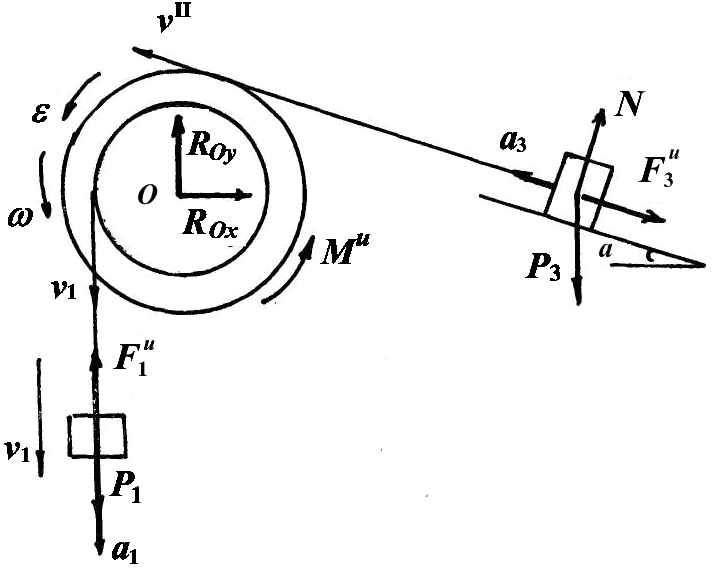
Рис. 2

Так как система пришла в движение из состояния покоя, то ускорения точек системы 1 направлены в сторону движения.

Приложим силы инерции. Тела 1 и 3 движутся поступательно, силы инерции этих тел выражаются векторами

и показываются на расчетной схеме противоположно ускорениям.

Силы инерции блока 2, вращающегося вокруг неподвижной оси Oz с угловым ускорением , приводятся к паре, момент которой равен

и изображается на схеме в сторону противоположную .

2. Выбор теоремы.

Применим общее уравнение динамики

.

Произведение силы, перемещения точки приложения силы и косинуса угла, который образуют сила и направление движения, представляет собой работу силы на данном перемещении.

Работа силы на заданном перемещении равна нулю, если точка приложения силы неподвижна или сила перпендикулярна направлению движения.

3. Составление уравнения.

, (1)

где - возможное перемещение тела 1, - угол поворота блока 2, -возможное перемещение центра масс тела 3 по направлению скорости, -высота, на которую поднимется центр масс тела 3 при перемещении на .

Уравнения связей. В общее уравнение динамики входят неизвестные перемещения. Выразим скорости центров масс и угловую скорость тел системы через скорость тела 1. Зависимости между возможными перемещениями такие же, как и между соответствующими скоростями.

Скорость любой точки обода блока малого радиуса равна скорости тела 1, а также произведению угловой скорости тела 2 и радиуса вращения .

,

отсюда

. (2)

Вращательная скорость любой точки обода блока большого радиуса с одной стороны, равна произведению угловой скорости блока и радиуса вращения R, а с другой - скорости тела 3.

.

Подставляя значение угловой скорости, получим

. (3)

Проинтегрируем при нулевых начальных условиях равенство (2) и (3) и получим соотношения возможных перемещений точек системы

.

Подставим полученные возможные перемещения в (1) и произведем замену

.

Поделив обе части равенства на запишем

Модули силы инерции: тела 1 ; тела 2 .

Момент пары сил инерции

.

Связь между ускорениями точек системы получим, продифференцировав по времени уравнения (2) и (3)

.

Тогда силы инерции точек системы запишутся

; .

Момент инерции блока

.

Тогда

.

Сила трения скольжения

.

В выражение (4) подставим значения сил инерции, силы трения и учитывая, что , запишем

.

4. Определение неизвестных.

.

Откуда

.

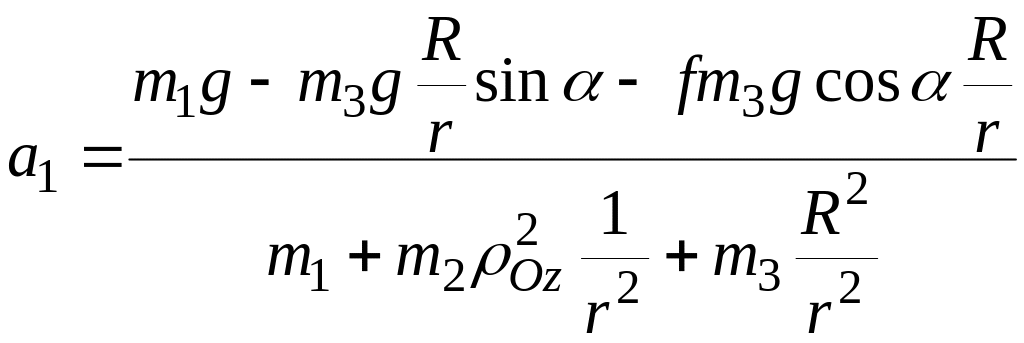Окончательно

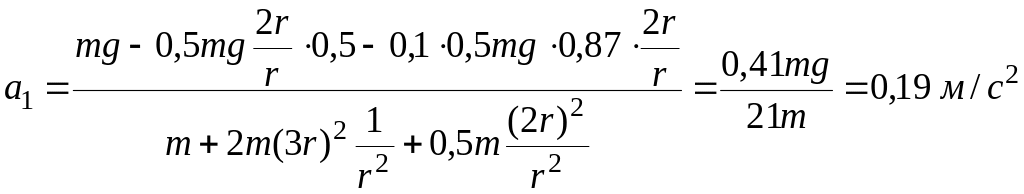
Для определения натяжения в ветви 1 - 2 мысленно разрежем нить и заменим ее действие на груз 1 реакцией .

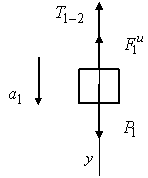
Общее уравнение динамики

.

Откуда

.

Пример. Составить дифференциальное уравнение движения механической системы, состоящей из груза 1, блока 2 и катка 3, имеющих соответственно массы т₁, т₂, т₃, и пружины с коэффици­ентом жесткости с (рис. 9.1). Груз и каток, расположенные на наклонных плоскостях, составляющих с горизонтом углы и , связаны невесомой и нерастяжимой нитью, перекинутой через блок. Тре­нием груза о плоскость, массой пружины и сопротивлением каче­нию пренебречь. Проскальзывание нити на блоке отсутствует. Каток катится без скольжения. Блок считать однородным цилиндром, мо­мент инерции катка относительно центральной оси равен , радиусы ступеней катка R и r.

Решение. Рассматриваемая система имеет одну степень свобо­ды при выполнении следующих условий:

1. Тела, входящие в систему, абсолютно твердые.

2. Нить нерастяжимая и при движении системы всегда натянута.

3. Проскальзывание нити на блоке отсутствует.

4. Каток катится без скольжения.

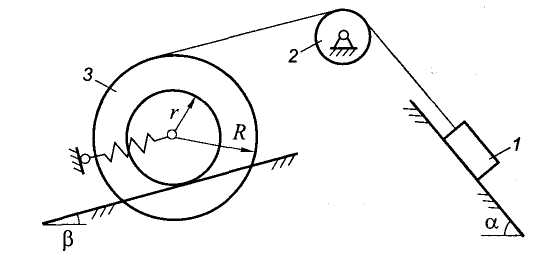
Рис. 9.1

Будем определять положение системы с помощью координаты х, направив соответствующую ось Ох параллельно наклонной плос­кости, на которой расположен груз. Начало оси совместим с поло­жением центра масс груза при равновесии системы (рис. 9.2). Пусть , и - соответствующие координате х углы поворота блока и катка и смещение центра масс катка от положения его равновесия. Легко установить, что (точка P₃, - МЦС катка)

(9.3)

где - радиус блока.

Для составления дифференциального уравнения движения вос­пользуемся общим уравнением динамики. Построим расчетную схему задачи. Изобразим на рисунке активные силы , , , реакцию неидеальной связи (пружины) ; приложим к телам сис­темы силы инерции.

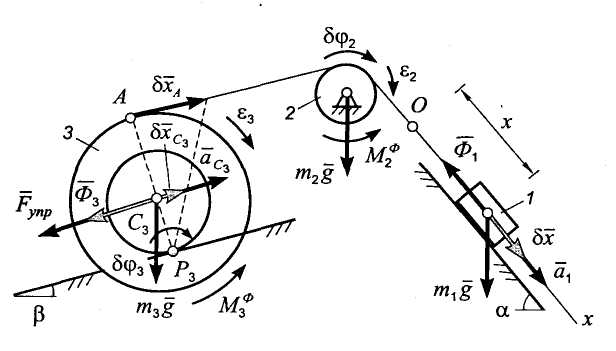
Рис. 9.2

Груз движется поступательно. Силы инерции его частиц эквива­лентны равнодействующей

, (9.4)

приложенной в центре масс ( - ускорение груза).

Блок вращается вокруг главной центральной оси инерции. Силы инерции его частиц эквивалентны паре сил с моментом

, (9.5)

где - момент инерции блока относительно оси вращения.

Вектор направлен по оси вращения блока противоположно вектору углового ускорения . На расчетной схеме это отражено дуговыми стрелками противоположного направления.

Каток совершает плоское движение. Силы инерции его частиц эквивалентны системе, состоящей из одной силы

, (9.6)

приложенной в центре масс катка ( - ускорение центра масс), и пары сил с моментом

, (9.7)

где - угловое ускорение катка.

Сообщим грузу возможное перемещение . Возможным пере­мещением блока является поворот на угол вокруг собственной оси. Возможным перемещением катка является поворот на угол вокруг оси, проходящей через мгновенный центр скоростей Р₃ пер­пендикулярно плоскости рисунка. Векторы и направлены по соответствующим осям, на расчетной схеме направления воз­можных поворотов блока и катка показаны дуговыми стрелками.

Запишем общее уравнение динамики

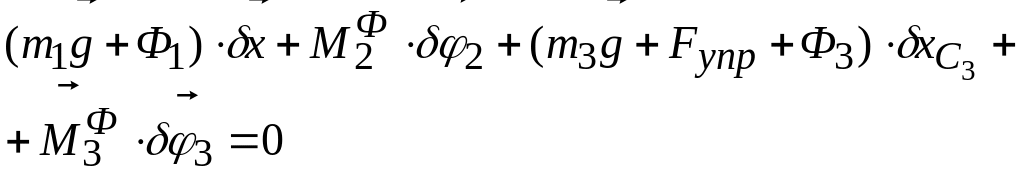. (9.8)

Заметим, что элементарная работа силы равна нулю, так как равно нулю возможное перемещение точки ее приложения.

Подставив в уравнение (9.8) формулы (9.4)-(9.7) и раскрыв ска­лярные произведения, получим

. (9.9)

Используя формулы (9.3), находим

(9.10)

(9.11)

Подставляя формулы (9.10) и (9.11) в уравнение (9.9), находим после сокращения на и простых преобразований:

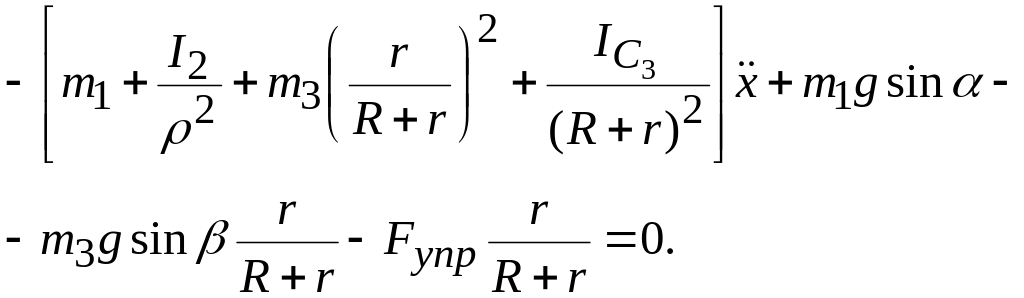(9.12)

Из уравнения (9.12) легко получить условие равновесия систе­мы. Действительно, поскольку

, (9.13)

где - статическая деформация пружины, то, подставляя (9.13) в уравнение (9.12) и имея в виду, что при равновесии x = 0, = 0, на­ходим

. (9.14)

С учетом условия (9.14) уравнение (9.12) принимает вид

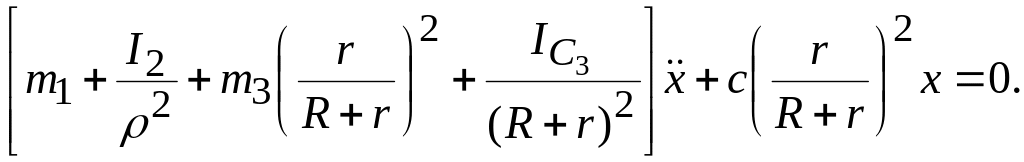(9.15)

Назовем приведенной массой и приведенной жесткостью величины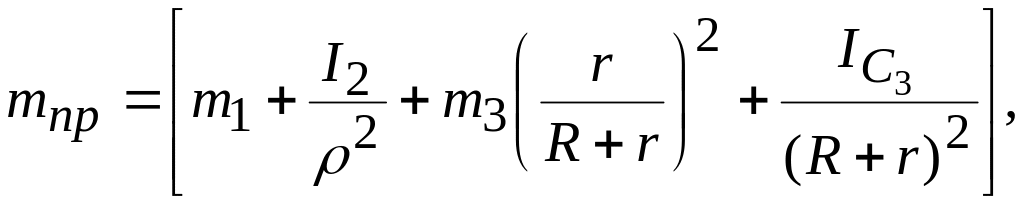

.

Тогда дифференциальное уравнение (9.15) можно записать в виде

, (9.16)

где

.

Пример. Груз 3 массы т₃ поднимается с помощью устройства, состоящего из шкивов 1 и 2, связанных невесомым ремнем (рис. 9.3). К ведущему шкиву 1 радиуса R₁ при­ложена пара сил с посто­янным моментом М. Оп­ределить угловое уско­рение ведущего шкива, если R₂, r₂ - радиусы ступеней ведомого шки­ва; I₁ и I₂ - моменты инерции шкивов относи­тельно осей их вращения. Сопротивлением и мас­сой троса пренебречь.

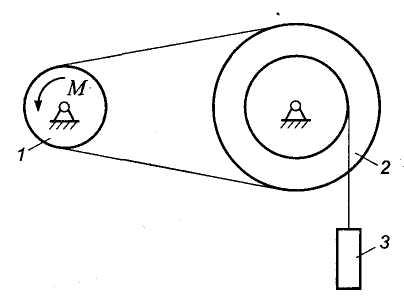
Рис. 9.3

Решение. Рассмат­риваемая механическая система имеет одну степень свободы, если выполняются следующие условия:

1. Тела 1, 2, 3 - абсолютно твердые.

2. Ремень и трос нерастяжимые.

3. Проскальзывание ремня на шкивах отсутствует.

4. Груз поднимается, не раскачиваясь (по направляющим).

Построим расчетную схему задачи. Связи, наложенные на сис­тему, являются идеальными. Поэтому на расчетной схеме (рис. 9.4) показаны только активные силы (вращающий момент и силы тяже­сти тел) и силы инерции.

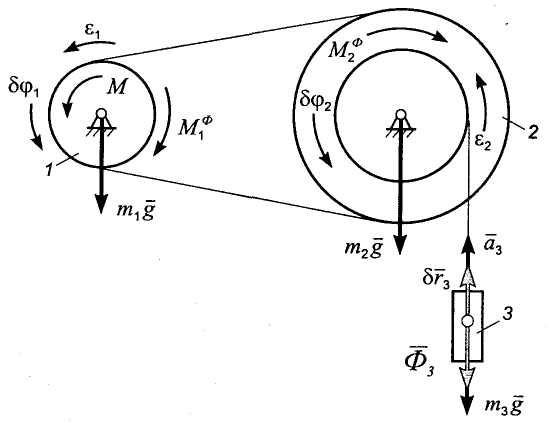
Рис. 9.4

Шкив 1 вращается вокруг своей главной центральной оси инер­ции. Поэтому система сил инерции его частиц эквивалентна паре сил, момент которой направлен противоположно угловому ускоре­нию шкива и имеет величину

. (9.17)

Шкив 2 также вращается вокруг своей главной центральной оси инерции. Поэтому система сил инерции его частиц эквивалентна паре сил, момент которой направлен противоположно угловому ускорению шкива и имеет величину

. (9.18)

Груз движется поступательно. Система сил инерции частиц гру­за эквивалентна равнодействующей силе, которая приложена в цен­тре масс, направлена противоположно его ускорению и имеет вели­чину

. (9.19)

Сообщим шкиву 1 возможное перемещение . Шкив 2 и груз 3 получат при этом возможные перемещения и соответствен­но. Запишем общее уравнение динамики

. (9.20)

Нетрудно установить, что

, (9.21)

. (9.22)

Подставив формулы (9.17)-(9.19), (9.22) в уравнение (9.20), по­лучим, с учетом (9.21), уравнение

.

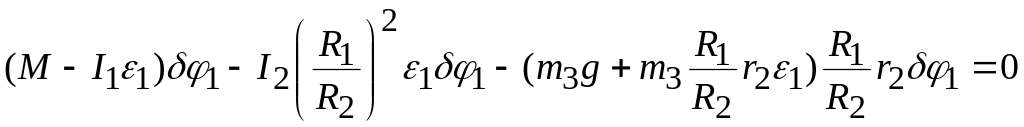из которого, после сокращения на находим

.

.

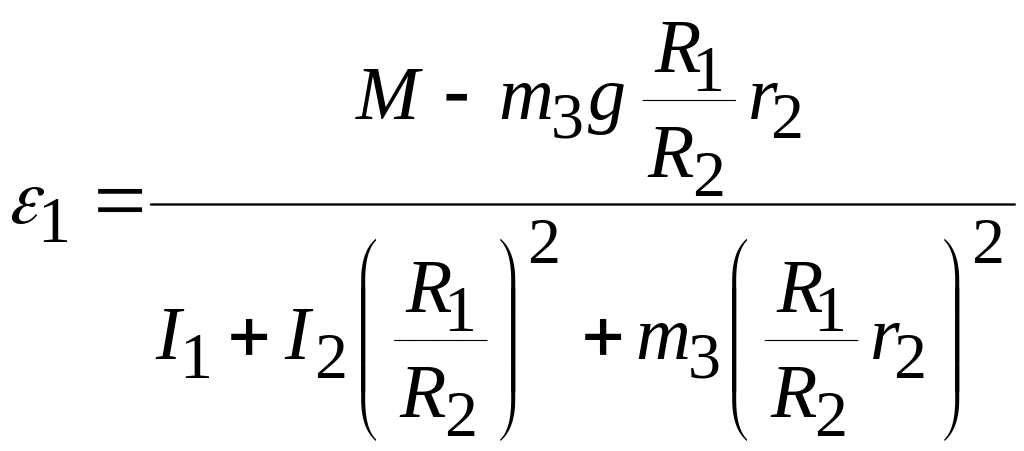Пример. Центробежный регулятор (рис. 9.5) вращается с постоянной угловой скоростью . Найти зависимость между угловой скоростью регулятора и углом отклонения его стержней 1 от вертикали, если муфта С массы М отжимается вниз пружиной 2, находящейся при = 0 в не деформированном состоянии и закреплен­ной верхним концом на оси регулятора.

Массы шаров А и В равны т, длина стержней равна l, оси подвеса стержней отстоят от оси регулятора на расстоянии а. Массами стержней и пружины, а также сопротивлением пренебречь. Коэффициент жесткости пружины равен с (И.В. Мещерский. Сборник задач по теоретической механике. М.: Наука, 1981. Задача №47.17).

Решение. Рассматриваемая система имеет две степени свободы. В качестве обобщенных координат примем угол поворота регуля­тора вокруг основной оси и угол отклонения стержней от вертика­ли. Закон изменения первой координаты задан: .

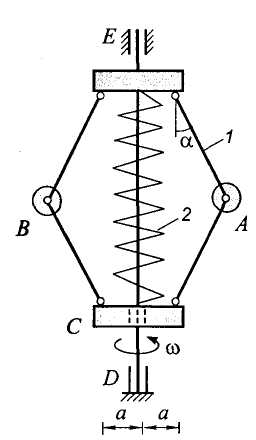
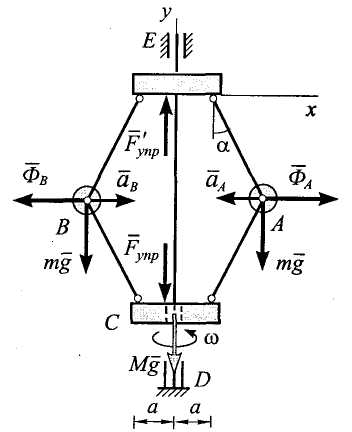
Рис. 9.5 Рис. 9.6

Построим расчетную схему задачи. Изобразим на рис. 9.6 активные силы (силы тяжести шаров и муфты), реакции пру­жины и (пружина - неидеальная связь) и силы инерции шаров , . Шары принимаем за материальные точки; силы инерции шаров направлены соответственно противоположно их ускорени­ям , и имеют величины

,

где

.

Таким образом,

. (9.23)

Для ответа на вопрос, поставленный в задаче, достаточно сооб­щить системе независимое возможное перемещение , и составить общее уравнение динамики в виде (9.2):

. (9.24)

Запишем координаты точек приложения сил относительно ко­ординатных осей ху, скрепленных с регулятором:

и вычислим их вариации

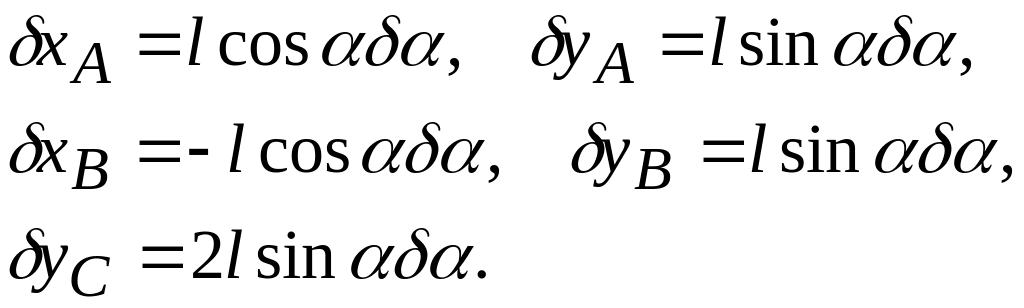. (9.25)

Подставляя формулы (9.23) и (9.25) в уравнение (9.24) и учиты­вая, что , получаем после простых преобразований:

.

Пример. Рейки 1 и 2 массы m₁ и т₂ движутся в параллельных направляющих, расположенных в горизонтальной плоскости (рис. 9.7). К рейке 2 прикреплен конец пружины 4, коэффициент жесткости которой с. Другой конец пружины закреплен неподвиж­но. Рейки находятся в зацеплении с диском 3, имеющим централь­ный момент инерции I₃, массу т₃ и радиус r. К диску приложена пара сил с моментом М.

Составить дифференциальные уравнения движения системы (Сборник задач по теоретической механике /Под ред. К.С. Колесни­кова. М.: Наука, 1983. Задача № 12.26).

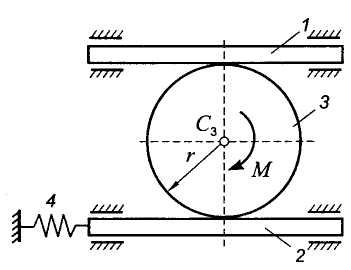
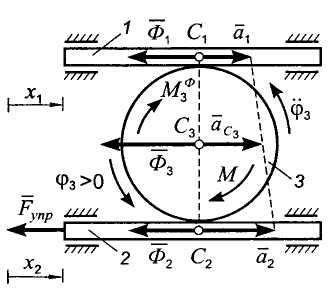
Рис. 9.7 Рис. 9.8

Решение. Рассматриваемая механическая система имеет две степени свободы. Будем определять ее положение с помощью коор­динат х₁ и х₂ (рис. 9.8). Угол поворота диска отсчитываем против хода часовой стрелки. При х₁ = 0, х₂=0 пружина не деформирована.

Изобразим на расчетной схеме:

1) активные силы - пару сил с моментом М (силы тяжести не по­ казаны, так как механизм расположен в горизонтальной плоскости);

2) реакцию пружины (неидеальная связь) - ;

3) силы инерции реек

, (9.26)

приложенные соответственно в центрах масс реек С₁ и С₂ и направ­ленные противоположно их ускорениям и ;

4) силы инерции частиц диска, совершающего плоское движение, эквивалентные системе, состоящей из силы и пары сил:

, (9.27)

где , - соответственно ускорение центра масс и угловое уско­рение диска; момент инерционной пары , перпендикулярный плоскости механизма, изображен на рисунке дуговой стрелкой.

Сообщим системе последовательно каждое из независимых воз­можных перемещений: , ; , .

Пусть сначала , (рис. 9.9).

Возможным перемещением диска является поворот вокруг точки Р₃ на угол (с учетом направления отсчета угла )

(9.28)

при этом центр масс диска име­ет возможное перемещение

. (9.29)

Запишем общее уравнение динамики

. (9.30)

Раскрыв скалярные произведения в уравнении (9.30) с учетом формул (9.26) и (9.27), получим

. (9.31)

Заметив, что

. (9.32)

Подставляя формулы (9.28), (9.29) и (9.32) в уравнение (9.31), получаем после простых преобразований второе дифференциальное уравнение движения системы:

. (9.33)

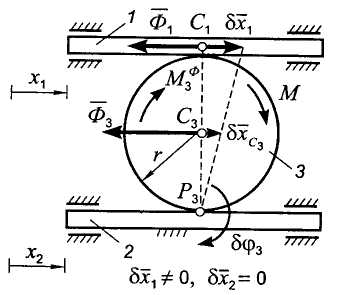
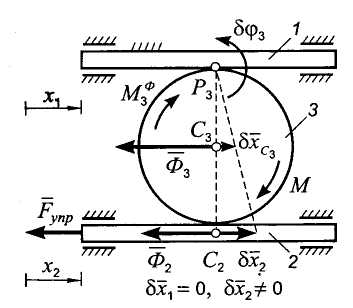
Рис. 9.9 Рис. 10

Пусть теперь , (рис. 9.10).

Возможным перемещением диска является поворот вокруг точки Р₃ на угол

, (9.34)

при этом центр масс диска име­ет возможное перемещение

. (9.35)

Запишем общее уравнение динамики

. (9.36)

Раскрыв скалярные произведения в уравнении (9.36) с учетом формул (9.26) и (9.27), получим:

. (9.37)

Подставляя формулы (9.32), (9.34) и (9.35) в уравнение (9.37), получаем после простых преобразований второе дифференциальное уравнение движения системы:

. (9.38)

Таким образом, движение рассматриваемой механической сис­темы описывается совокупностью двух дифференциальных уравне­ний (9.33) и (9.38).

Пример. Груз 7 массы т₇ поднимается по наклонной плоскости, образующей с горизонтом угол , с помощью невесомого и нерастяжимого троса, перекинутого через блок 6 и навиваемого на барабан 5 радиусе r (рис. 9.11). Передаточный механизм состоит из двух пар зубчатых колес: цилиндрических 1, 2 и конических 3, 4. Колесо 1 находится на ведущем валу I, колесо 2 и 3 расположены на ведомом валу II, колесо 4 и барабан находятся на валу III. К ведущему валу приложен со стороны мотора постоянный вращающий момент М. Определить ускорение груза, если z₁, z₂, z₃, z₄ - числа зубьев колес; R - радиус блока; I₁, I_II, 1_III - моменты инерции валов (вместе с распо­ложенными на них деталями) относительно осей вращения; М_с - по­стоянный момент сопротивления на оси блока; f - коэффициент тре­ния скольжения груза о плоскость. Центры масс вращающихся тел расположены на осях вращения. Массой блока пренебречь.

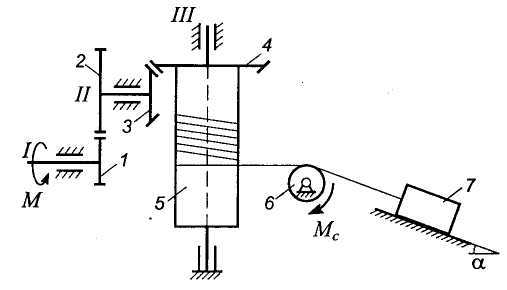
Рис. 9.11

Решение. Рассматриваемая система при выполнении следую­щих условий: 1) тела, входящие в ее состав, абсолютно твердые; 2) трос нерастяжимый; 3) проскальзывание троса на блоке отсутству­ет - имеет одну степень свободы. В качестве обобщенной координаты можно принять угол поворота ведущего вала или, с учетом цели зада­чи, параметр х, определяющий положение груза на плоскости.

Составим дифференциальное уравнение движения системы с помощью общего уравнения динамики. Изобразим на расчетной схеме (рис. 9.12) задаваемые силы: вращающий момент М; силы тяжести валов , , и груза ; момент сопротивления М_с и реакцию неидеальной связи (плоскости) - силу трения . Прило­жим к телам системы силы инерции. Поскольку оси вращения валов являются главными центральными осями инерции этих тел, то сис­темы сил инерции частиц валов эквивалентны парам сил, моменты которых имеют направление, противоположное угловым ускорениям , , соответственно, а их величины вычисляются по формулам:

. (9.39)

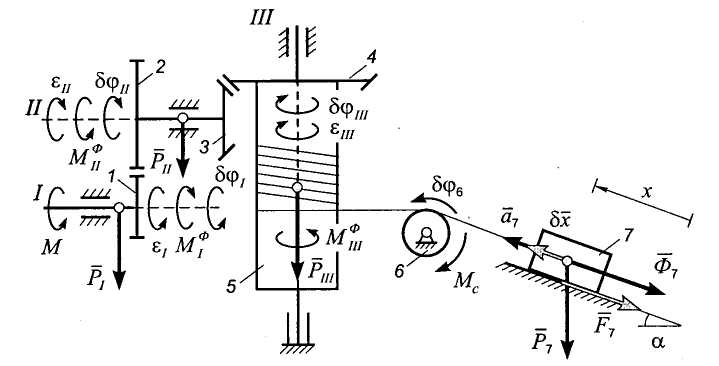
Рис. 9.12

Поскольку массой блока пренебрегаем, то никаких сил инерции к этому телу прикладывать не надо. Силы инерции частиц груза, движущегося поступательно, эквивалентны одной силе, направлен­ной противоположно его ускорению , приложенной в центре масс и имеющей величину

. (9.40)

Сообщим ведущему валу возможное перемещение , направ­ленное в сторону вращающего момента. Вал II получит при этом воз­можное перемещение , вал III - возможное перемещение , блок - возможное перемещение , груз - возможное перемещение . Составим общее уравнение динамики, т.е. вычислим сумму эле­ментарных работ задаваемых сил, силы трения и сил инерции на воз­можных перемещениях точек их приложения и приравняем ее нулю:

(9.41)

Преобразуем уравнение (9.41). Выразим возможные перемеще­ния через 8х, а ускорения, входящие в силы инерции (см. формулы (9.39), (9.40)), - через . Имеем

,

где r₁, r₂, r₃, r₄ - радиусы колес.

Отсюда

. (9.42)

По аналогии с последними формулами

(9.43)

Подставляя формулы (9.39), (9.40), (9.42) и (9.43) в уравнение (9.41) и учитывая, что , находим

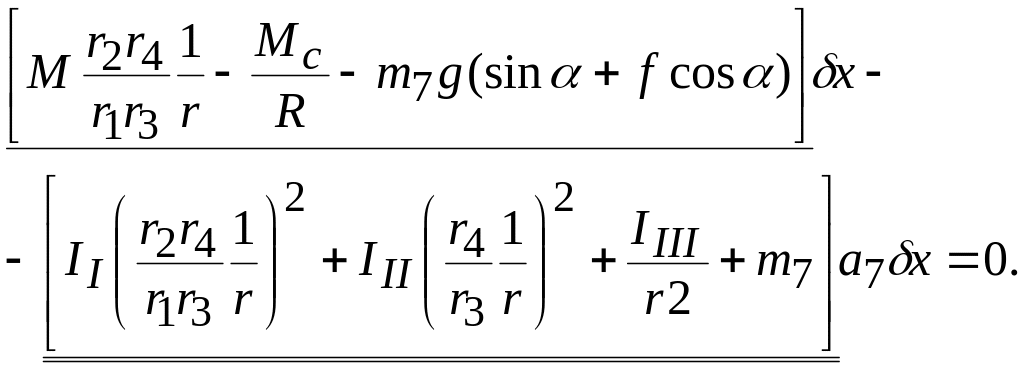(9.44)

Сокращая на , получаем дифференциальное уравнение движе­ния системы ( ):

, (9.45)

где через F_np и т_пр обозначены выражения, стоящие в квадратных скобках в уравнении (9.44), подчеркнутые соответственно одной и двумя линиями. Приведенная масса т_пр и приведенная сила F_np яв­ляются величинами постоянными. Следовательно, груз поднимается с постоянным ускорением. Поскольку радиусы колес и их числа зубьев - величины пропорциональные, то отношения радиусов мож­но заменить отношениями соответствующих чисел зубьев. Поэтому

.

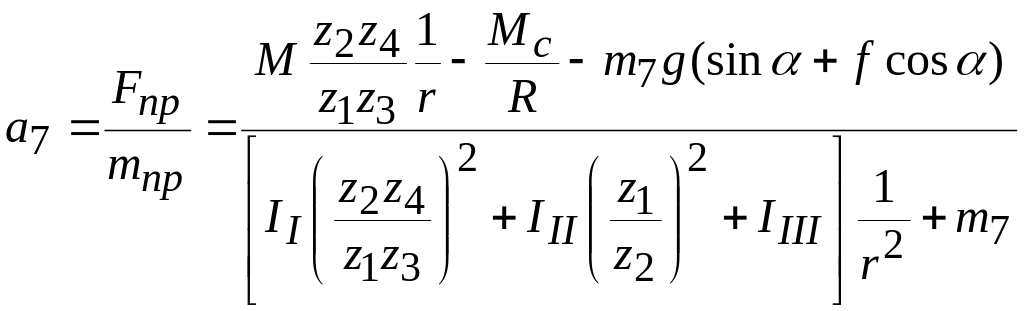Пример. Определить закон малых колебаний однородного прямолинейного стержня массы т, закрепленного в точке А с помо­щью цилиндрического шарнира и поддерживаемого в точке D вер­тикальной пружиной жесткости с (рис. 9.13). Размеры указаны на рисунке. Сопротивление не учитывать. При рав­новесии стержень зани­мает горизонтальное положение. В начальный момент стержню из со­стояния покоя сообщена угловая скорость , на­правленная против хода часовой стрелки.

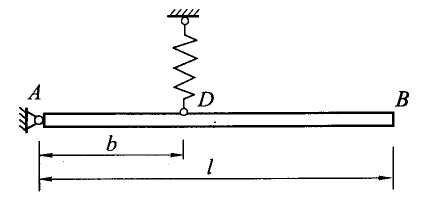
Рис. 9.13

Решение. Система имеет одну степень свободы. Примем в каче­стве обобщенной координаты угол поворота стержня , который будем отсчитывать от равновесного положения стержня по ходу часовой стрелки. Составим дифференциальное уравнение малых колебаний стержня с помощью общего уравнения динамики.

Расчетная схема приведена на рис. 9.14. На ней изображены стержень в произвольном положении с положительной координатой , сила тяжести , реакция пружины и силы инерции. Система инерционных сил частиц стержня эквивалентна совокупности одной силы, приложенной в центре масс, и одной пары. Сила инерции представлена ее составляющими: центробежной силой , направ­ленной противоположно нормальному ускорению центра масс и имеющей величину , где - угловая скорость стержня, и тангенциальной силой , направленной противополож­но тангенциальному ускорению центра масс и имеющей величину

, (9.46)

где - угловое ускорение стержня; предполагается, что в рассмат­риваемом положении стержня > 0.

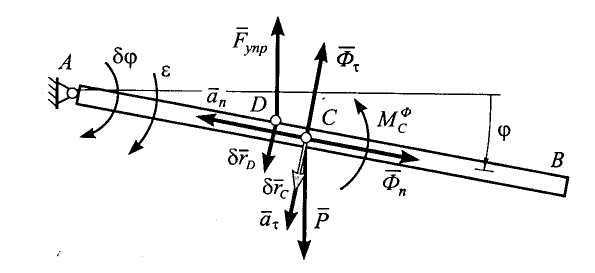
Рис. 9.14

Инерционная пара сил имеет момент, направленный противопо­ложно угловому ускорению стержня, а его величина

, (9.47)

где - момент инерции стержня относительно оси, про­ходящей через центр масс.

Угол поворота стержня считаем малым, поэтому отклонением упругой силы от вертикали пренебрегаем. Удлинение пружины равно , где - статическое удлинение пружины; Ь - отклонение точки D от равновесного положения. Таким образом,

. (9.48)

Шарнир А является идеальным, поэтому его реакции на расчетной схеме не показаны.

Сообщим стержню возможное перемещение в направлении возрастания обобщенной координаты. Точки приложения сил полу­чат при этом возможные перемещения и , перпендикуляр­ные к оси стержня, величины которых пропорциональны расстояни­ям точек от оси вращения:

. (9.49)

Запишем общее уравнение динамики. Для этого вычислим сумму элементарных работ сил, изображенных на расчетной схеме, на воз­можных перемещениях точек их приложения и приравняем ее нулю:

.

Заметим, что элементарная работа центробежной силы инерции равна нулю, так как . Подставляя в последнее уравнение формулы (9.46)-(9.49) и учитывая, что при малых колебаниях , получаем

. (9.50)

Сокращая на и учитывая, что при равновесии стержня вы­полняется условие

,

записываем, после несложных преобразований, уравнение (9.50) в виде

, (9.51)

где — циклическая частота колебаний.

Таким образом, малые колебания стержня описываются линей­ным дифференциальным уравнением (9.51), общее решение которого

(9.52)

содержит две постоянные интегрирования С₁ и С₂, определяемые по начальным условиям

. (9.53)

Производная

. (9.54)

Удовлетворяя условиям (9.53) в (9.52) и (9.54), находим

.

Подставляя значения постоянных интегрирования в общее решение (9.52), получаем закон движения стержня

.

Таким образом, стержень совершает гармонические колебания амплитуды и периода .

Пример. Зубчатое колесо 1 радиуса r, находящееся в зацепле­нии с рейкой 2 массы т, вращается вокруг горизонтальной оси С₁ под действием пары сил, имеющей постоянный момент М (рис. 9.15). Рейка перемещается в вертикальных направляющих, преодолевая постоянную силу сопротивления . Центр масс колеса расположен на оси вращения. Момент инерции колеса относительно оси враще­ния равен I. Определить угловое ускорение колеса.

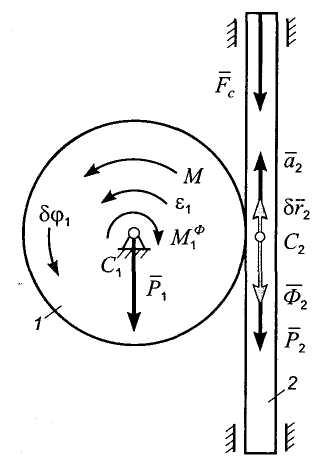
Рис. 9.15

Решение. Рассмотрим систему, состоящую из колеса и рейки. Эта система имеет одну степень свобо­ды. Будем определять положение системы с помощью угла поворота колеса, отсчитывая его в направ­лении вращения последнего.

Составим дифференциальное уравнение движения системы. Рас­четная схема приведена на рис. 9.15. Поскольку связи, наложенные на систему, являются идеальными, то на расчетной схеме изображены заданные силы - силы тяжести ко­леса и рейки и , сила сопро­тивления и силы инерции. Так как колесо вращается вокруг глав­ной центральной оси инерции, то система сил инерции его частиц эквивалентна паре сил, момент которой направлен противоположно угловому ускорению колеса и имеет величину

. (9.55)

Система сил инерции частиц рейки, движущейся поступательно, эквивалентна одной силе , которая приложена в центре масс рейки, направлена противоположно его ускорению и имеет величину

. (9.56)

Сообщим колесу возможное перемещение 5 возможное пере­мещение рейки при этом будет

. (9.57)

Запишем общее уравнение динамики

.

Сила тяжести колеса не вошла в это уравнение, так как воз­можное перемещение точки ее приложения равно нулю.

Подставляя в последнее уравнение формулы (9.55)-(9.57), по­лучаем после простых преобразований с учетом того, что , дифференциальное уравнение движения системы

,

где

.

Таким образом, колесо вращается с постоянным угловым уско­рением

.

Пример. Составить дифференциальные уравнения малых движений системы, состоящей из балки 1 массы _т1 и груза 2, скреп­ленного с балкой с помощью цилиндрического шарнира в точке С (рис. 9.16).

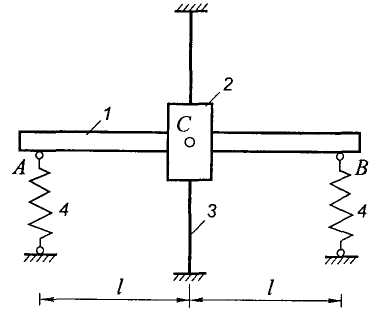
Рис. 9.16

Груз, имеющий массу т₂, перемещается по верти­кальной направляющей 3. Балка поддерживается дву­мя пружинами 4 жесткости с. Размеры указаны на рис. 9.16. Массу пружин и со­противление не учитывать. Центры масс балки и груза совпадают и находятся в точке С. Момент инерции балки относительно оси, проходящей через ее центр масс, равен I.

Решение. Система имеет две степени свободы. Будем опреде­лять ее положение с помощью двух независимых параметров: коор­динаты х, задающей положение центра масс системы и отсчитывае­мой вертикально вниз от его равновесного положения, и угла поворота балки. Угол отсчитываем от горизонтального направления против хода часовой стрелки. Составим дифференциальные уравне­ния движения системы с помощью общего уравнения динамики.

Построим расчетную схему (рис. 9.17). Изобразим систему в произвольном положении с положительными координатами х и , покажем на рисунке равнодействующую сил тяжести балки и груза , реакции пружин , и силы инерции систе­мы. Поскольку рассматриваются малые движения системы, то мож­но считать, что оси пружин при движении остаются вертикальными, а траекториями точек крепления пружин с балкой являются верти­кальные отрезки прямых АА₀ и ВВ₀ (точки А₀ и В₀ соответствуют равновесному положению верхних концов пружин). Указанные от­резки складываются из двух частей: поступательного перемещения вместе с центром масс, равного х, и перемещения при вращении во­круг центра масс, равного , т.е. , а , поэтому

, (9.58)

где - статическая деформация пружин.

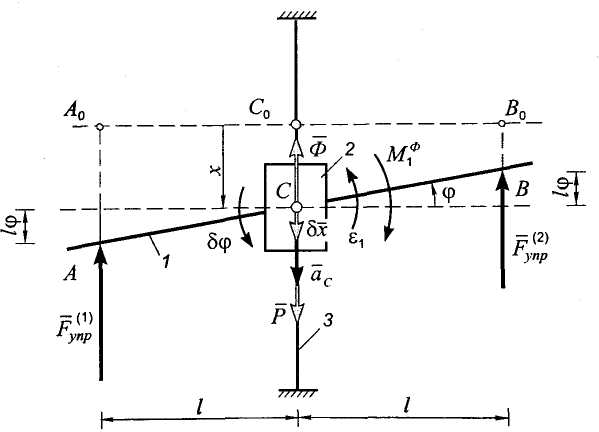
Рис. 9.17

Балка совершает плоское движение. Поэтому силы инерции ее частиц эквивалентны совокупности, состоящей из силы

,

приложенной в центре масс, где - ускорение центра масс, и па­ры, имеющей момент

,

где - угловое ускорение балки.

Сила инерции груза, движущегося поступательно, приложена в центре масс и определяется по формуле

.

На расчетной схеме показана равнодействующая

.

Сообщим теперь системе возможное перемещение, на котором изменяются обе обобщенные координаты, т.е. , , и запи­шем общее уравнение динамики. Для этого вычислим сумму элемен­тарных работ сил, изображенных на расчетной схеме, на возможных перемещениях точек их приложения и приравняем ее нулю. Возмож­ная работа сил тяжести запишется в виде ; воз­можная работа сил инерции ; работа инерци­онного момента .

Возможные перемещения точек приложения сил упругости складываются из двух составляющих: 1) поступательного переме­щения вместе с центром масс; и 2) перемещения при вращении вокруг центра масс. Во втором случае возможные перемещения пер­пендикулярны к оси балки, направлены в сторону и имеют вели­чину . Возможную работу каждой упругой силы вычислим как сумму ее работ на упомянутых перемещениях: и ; косинус в последних выражениях следует опустить, так как рассматриваются малые движения системы. Таким образом, с учетом формул (9.58), общее уравнение динамики можно записать в виде

(9 59)

Полагая в этом уравнении х = 0, =0, = 0, = 0, получаем ус­ловие равновесия системы

. (9.60)

Перепишем уравнение (9.59) с учетом (9.60), сгруппировав чле­ны, содержащие и :

. (9.61)

Поскольку система является голономной, то вариации обобщен­ных координат и суть независимые величины. Поэтому для получения дифференциальных уравнений движения системы следу­ет приравнять нулю выражения, стоящие в квадратных скобках в уравнении (9.61). После простых преобразований получаем

(9.62)

где

.

Таким образом, при малых колебаниях данной системы изме­нение координат х и описывается независимыми дифференци­альными уравнениями. Поскольку общие решения этих уравнений имеют вид

можно утверждать, что каждая из обобщенных координат колеблет­ся по гармоническому закону: координата х - с частотой , коорди­ната - с частотой .

Пример. Кривошип 1 длины r, вращающийся вокруг горизон­тальной оси О под действием пары сил с моментом М, приводит в движение с помощью ползуна 2 кулису 3, перемещающуюся по прямолинейным направляющим. Кулиса связана с центром колеса 4 радиуса R. Составить дифференциальное уравнение движения меха­низма, если т₂, т₃, т₄ - массы ползуна, кулисы и колеса, I - момент Инерции колеса относительно оси, проходящей через центр масс. Сопротивление движению и массу кривошипа не учитывать. Центр масс ползуна находится в точке А.

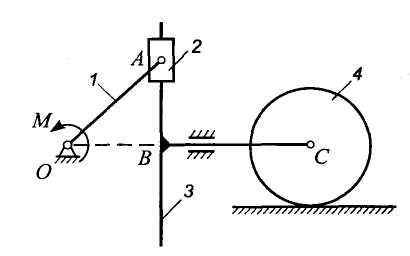
Рис. 9.18

Решение. Система имеет одну степень свободы при условии, что колесо катится без скольжения. Примем за обобщенную координату угол поворота кривошипа (рис. 9.19). Изобразим на расчетной схеме заданные силы: момент пары М и силы тяжести тел , , . Связи, наложенные на систему, являются идеальными, поэтому их реакции на расчетной схеме не показаны. Приложим к телам системы, обладающим массой, силы инерции. Ползун совершает круговое поступательное движение. Ускорение его центра масс

,

где - тангенциальное ускорение, - нормальное ускорение. В соответствии с этим силу инерции ползуна разложим на две составля­ющие: тангенциальную и нормальную .

i

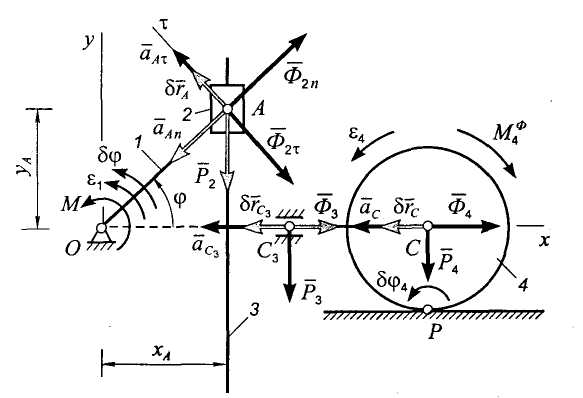
Рис. 9.19

Кулиса совершает прямолинейное поступательное движение, поэто­му система сил инерции ее частиц эквивалентна одной силе, прило­женной в центре масс С₃ и равной . Колесо совершает плоское движение. Система сил инерции его частиц эквивалентна силе , приложенной в центре масс колеса, и паре сил с моментом . В последних формулах -ускорение цен­тра масс колеса, - угловое ускорение колеса.

Сообщим кривошипу возможное перемещение 5 в направле­нии возрастания угла поворота; при этом центр масс ползуна полу­чит возможное перемещение , центр масс кулисы - . Воз­можным перемещением колеса является поворот на угол вокруг мгновенного центра скоростей (точки Р), при этом центр масс коле­са имеет перемещение 8. Запишем общее уравнение динамики

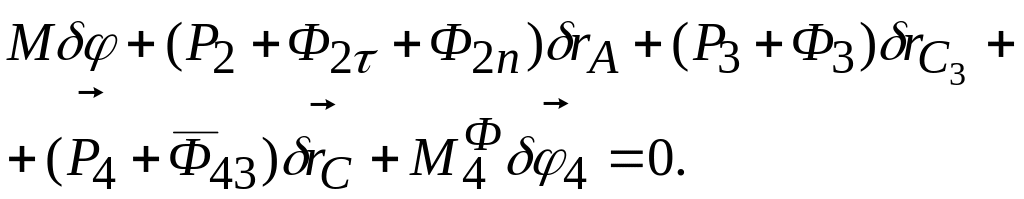(9.63)

Заметим, что , , , так как , , . Представляя другие скалярные произ­ведения в уравнении (9.63) через проекции векторов, получаем

. (9.64)

Ось Oz направлена к наблюдателю. Преобразуем уравнение (9.64). Прежде всего, заметим, что , . Проекция ускорения точки А на ось х определится соотношением:

.

Учитывая, что

,

имеем

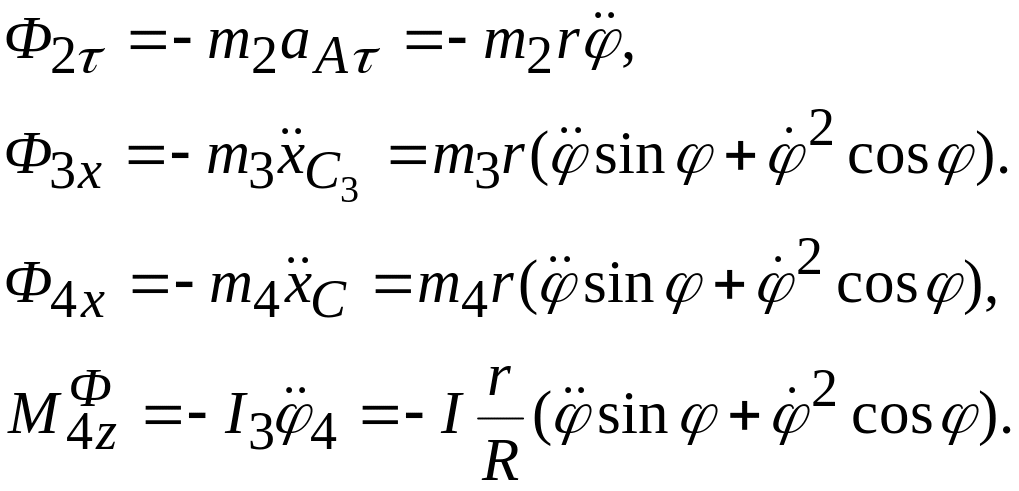(9.65)

Вариации координат

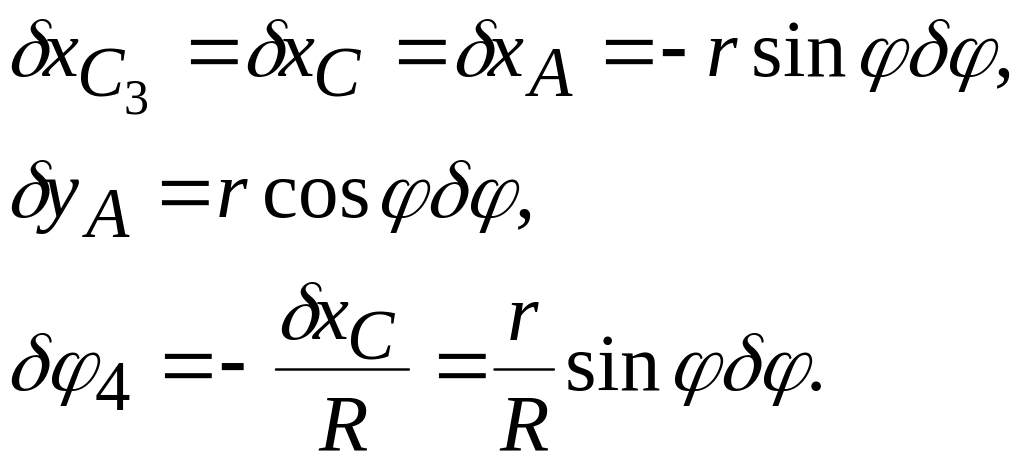(9.66)

Подставляя формулы (9.65) и (9.66) в уравнение (9.64) и учи­тывая, что , , получаем после неслож­ных преобразований дифференциальное уравнение движения ме­ханизма:

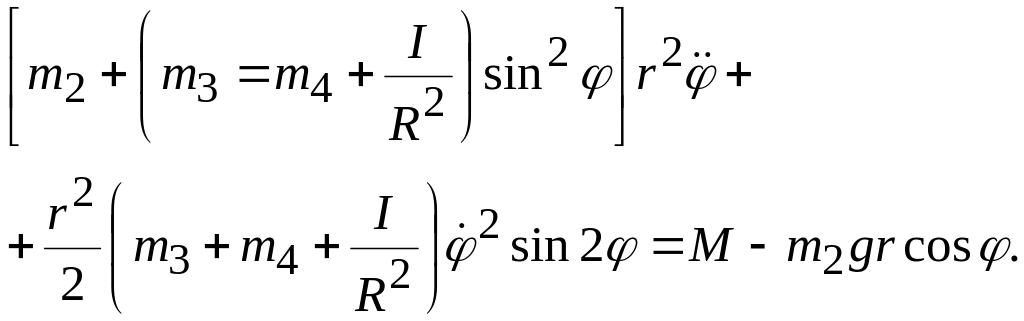
Пример. Брус 1 массы т₁ находится на гладкой горизонтальной плоскости. По брусу катится однородный цилиндр 2 под действием пары сил, имеющей постоянный момент М. Определить ускорение бруса, если т₂ - масса цилиндра, r - его радиус. Качение цилиндра происходит без скольжения.

Решение. Система имеет две степени свободы. Примем за обобщенные координаты величины х₁ и х₂. Координата х₁ задает по­ложение бруса относительно неподвижной системы координат хОу, а координата х₂ задает положение цилиндра относительно подвиж­ных осей х'О'у', скрепленных с брусом (рис. 9.20).

Изобразим на расчетной схеме заданные силы: момент пары М и силы тяжести тел , . Связи, наложенные на систему, являются идеальными, поэтому их реакции на расчетной схеме не показаны. Приложим к телам системы силы инерции. Брус совершает поступа­тельное движение. Система сил инерции его частиц эквивалентна одной силе

, (9.67)

приложенной в центре масс С₁ бруса. Колесо совершает плоское движение. Система сил инерции его частиц эквивалентна силе

, (9.68)

приложенной в его центре масс С₂, и паре сил, имеющей момент

. (9.69)

В формулах (9.67)-(9.69): - ускорение центра масс бруса; - ускорение центра масс цилиндра; - угловое ускорение ци­линдра; - момент инерции цилиндра относительно оси, проходящей через его центр масс.

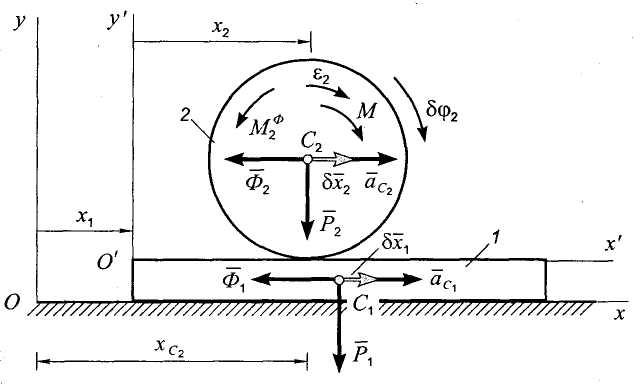
Рис. 9.20

Сообщим системе возможное перемещение , , при котором изменяются обе обобщенные координаты, и запишем общее уравнение динамики. Для этого вычислим сумму элементарных ра­бот активных сил и сил инерции на возможных перемещениях точек их приложения и приравняем ее нулю:

.

Первые два слагаемых в левой части последнего уравнения рав­ны нулю, так как силы тяжести перпендикулярны к возможным пе­ремещениям точек их приложения. Записывая остальные скалярные произведения через проекции векторов на оси неподвижной систе­мы координат, получаем

. (9.70)

Из формул (9.67)-(9.69) следует, что

. (9.71)

Поскольку , то

. (9.72)

Угловое ускорение цилиндра

. (9.73)

Кроме того,

. (9.74)

Подставляя формулы (9.71)-(9.74) в уравнение (9.70), получаем

,

или

.

Поскольку система является голономной, то вариации обобщен­ных координат - независимые величины. Приравнивая нулю выраже­ния, стоящие в квадратных скобках в последнем уравнении, получаем совокупность дифференциальных уравнений движения системы

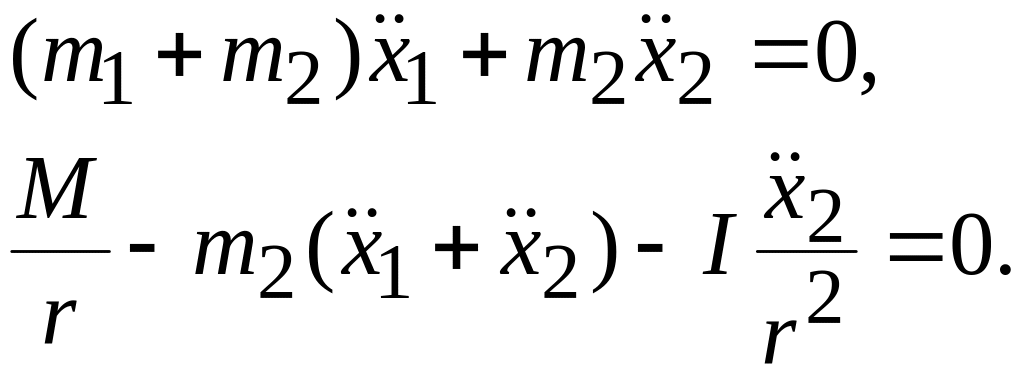(9.75)

ёИз первого уравнения находим

.

Подставляя эту формулу во второе уравнение системы (9.75), находим проекцию ускорения бруса на ось х:

Замечание. При движении имеет место сохранение проекции на ось х количества движения системы. Это следует из первого уравне­ния (9.75):

.