Выражение обобщенных сил через проекции сил на неподвижные оси декартовых координат. Случай сил, имеющих потенциал

Выражая скалярные произведения в формуле (13.8) через проекции векторов сомножителей на неподвижные оси декартовых координат, получим обобщенную силу Q_j в следующем виде:

. (13.17)

Рассмотрим случай, когда силы, действующие на механическую систему, имеют потенциал. Тогда проекции этих сил на оси координат равны взятым со знаком минус частным производным от потенциальной энергии по соответствующим координатам точек:

.

Подставим эти значения проекций сил в формулу (13.17):

. (а)

Потенциальная энергия механической системы яв­ляется функцией декартовых координат точек системы:

.

Декартовы координаты точек системы являются функциями ее обобщенных координат и времени:

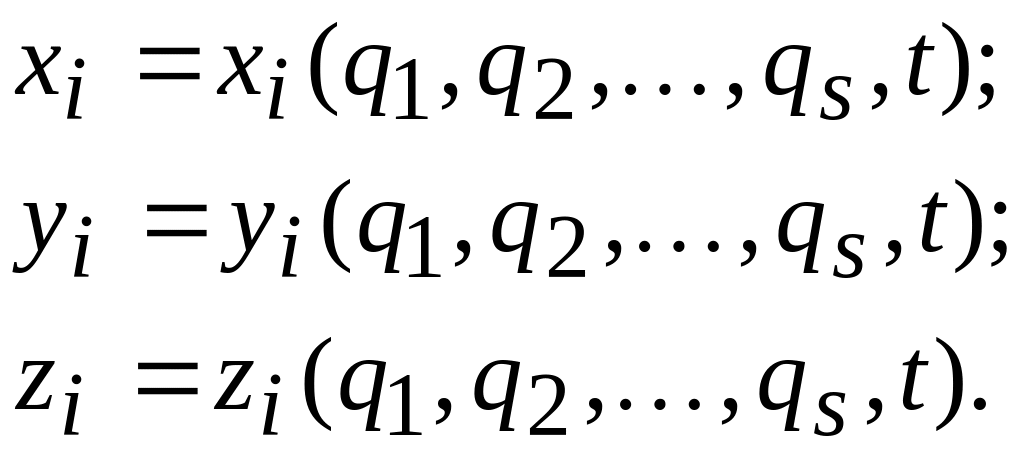
Потенциальная энергия П механической системы как функцию обобщенных координат и времени:

. (13.18)

В случае стационарных связей зависимость декартовых координат от обобщенных координат имеет вид

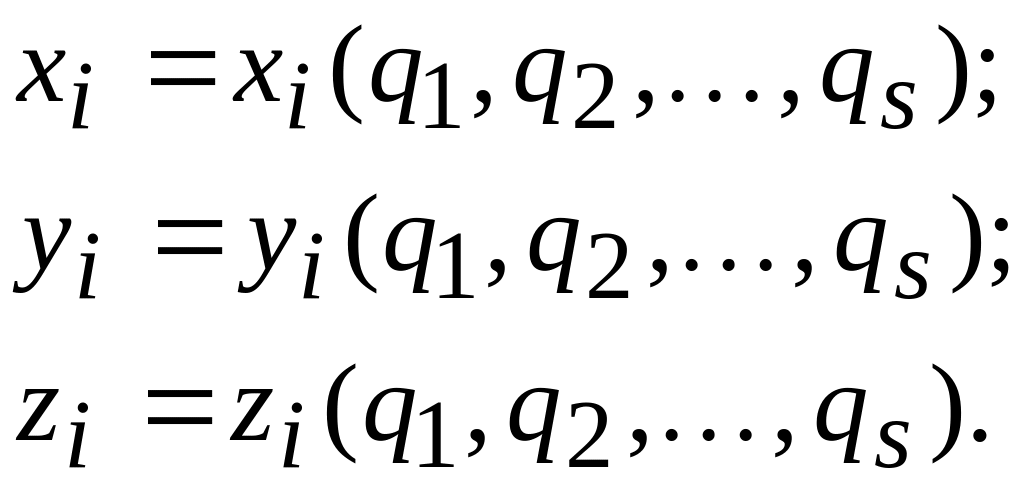
Потенциальная энергия системы в этом случае является функцией только обобщенных координат:

(13.19)

Найдем частную производную от потенциальной энергий системы П по обобщенной координате , рассматривая П как сложную функцию обобщенных координат. Эта производная определяется суммой 3n слагаемых. Каждое слагаемое равно произведению частной производной от П по одной из 3n декар­товых координат точек на производную от этой декартовой координаты по выбранной обобщенной координате :

. (б)

Сопоставляя выражения (а) и (б), устанавливаем:

. (13.20)

Формулы (13.20) показывают, что в случае сил, имеющих потенциал, обобщенная сила, соответствующая обобщенной координате q_j, равна взятой со знаком минус частной производной от потенциальной энергии механической системы по этой координате.

3. Общее уравнение динамики в обобщенных силах. Приведем общее уравнение динамики (13.4) к виду

.

На основании (13.12)

где - обобщенная сила системы сил, действующих на механическую систему, соответствующая обобщенной координате q_j; - обобщенная сила инерции, соответствующая обобщенной координате q_j.

Подставив эти значения в общее уравнение динамики (13.4), получаем

или . (13.21)

Приращения обобщенных координат δq_j произвольны и не зависят друг от друга. Поэтому в полученном уравнении (21) все коэффициенты при этих приращениях должны быть равны нулю. Приравняем нулю эти коэффициенты:

. (13.22)

Уравнения (13.22) эквивалентны общему уравнению динамики (13.21). Если силы, действующие на механическую систему, уравновешивают­ся, т. с. механическая система находится в состоянии покоя, или все ее точки движутся прямолинейно и равномерно, то силы инерции ее точек равны нулю. Следовательно, и обобщенные силы инерции системы равны нулю:

.

Тогда уравнения (13.22) принимают вид

. (13.23)

Равенства (13.23) выражают условия равновесия сил в обобщенных силах. Преобразуем условия равновесия (13.23) для консервативных сил, т.е. сил, имеющих потенциал. Для любой системы сил условия равновесия имеют вид

.

В случае консервативных сил обобщенные силы определяются формулами:

.

Следовательно, условия равновесия консервативной системы сил имеют вид

. (13.24)

Пример. Ползун А весом G₁ скользит вниз по гладкой наклонной плоскости, образующей с горизонтом угол а. К ползуну шарнирно прикреплен невесомый стержень длиной l с шариком B на конце; вес шарика G₂ (рис. 13.4).

Положение системы определяется обобщенными координатами s и φ, пока­занными на рис. 13.6. Определить обобщенные силы, соответствующие этим обобщенным координатам.

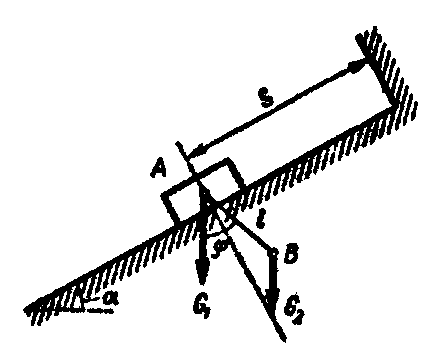
Рис. 13.4

Решение. Для определения обобщенных сил Q_s и Q_φ используем фор­мулу:

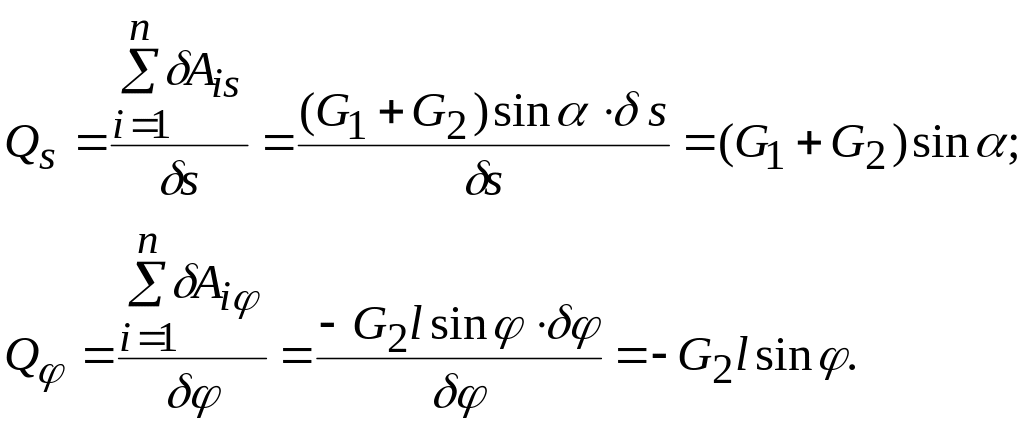
Пример. Груз А весом поднимается лебедкой с помощью троса по шероховатой наклонной плоскости, которая составляет с горизонтом угол . К валу лебедки В радиусом r приложены вращающий момент и момент трения (рис. 13.5). Зная, что коэффициент трения скольжения груза по плоскости равен f, и пренебрегая весом троса, определить обобщенную силу, приняв за обобщенную координату угол поворота вала лебедки.

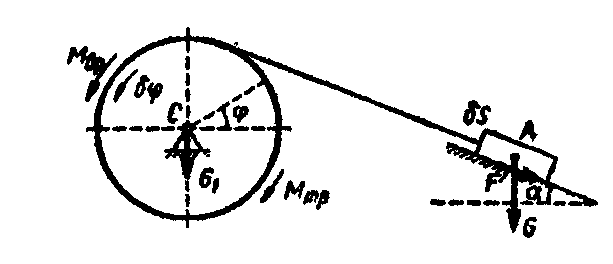
Рис. 13.5

Решение. Обобщенную силу соответствующую обобщенной коор­динате , можно определить как по формуле (13.8), так и по формуле (13.16). Для определения по формуле (13.8) сообщаем обобщенной координате приращение и составляем сумму работ моментов , , силы тяжести и силы трения на перемещениях, вызванных приращением угла поворота :

.

Так как , имеем

.

Тогда

.

Применяя формулу (13.16), в которую входят мощность системы сил, соответствующая возможной обобщенной скорости системы , получаем

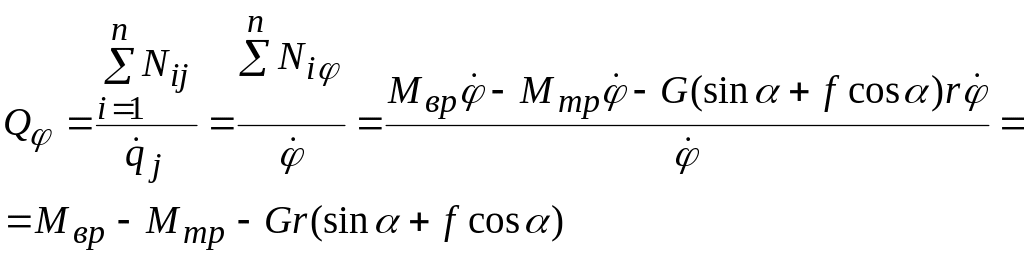
Разумеется, результат получился тот же.