3. Применение принципа возможных перемещений к простейшим машинам

Простейшие машины являются системами с одной степенью сво­боды. На машины действуют движущая сила , или вращающий момент и сила сопротивления , или момент сопротивления . Предположим, что силы (или моменты) и реакции имеющихся связей взаимно уравновешиваются. Для установления условий равновесия сил и машине сообщают возможное перемещение и составляют уравнение работ. На основании (12.6) условие равновесия сил и получает вид

, (12.9)

где - возможное приращение радиуса-вектора точки приложения силы , соответствующее ее возможному перемещению; - возмож­ное приращение радиуса-вектора точки приложения силы , соответ­ствующее ее возможному перемещению. Предположим, что возможное перемещение системы из состояния покоя происходит в течение ничтожно малого промежутка времени τ. Тогда точки приложения сил перемещаются со скоростями

и , (12.10)

называемыми возможными скоростями. Разделим уравнение работ (12.9) на величину τ:

.

Подставим сюда значение возможных скоростей точек:

,

или

.

Обозначим проекции сил и на направление соответствующих скоростей Р' и R', т.е.

;

тогда

.

Если направления Р' и совпадают, то направления R' и про­тивоположны. Пользуясь абсолютными величинами проекций, получим

,

отсюда

. (12.11)

Соотношение (12.11) можно выразить так: то, что выигрываться в силе, теряется в скорости. Это положение, установленное Галилеем, носит название золотого правила механики. Рассмотрим некоторые простейшие машины.

Полиспасты. Полиспаст состоит из двух систем блоков, каждая из которых помещена в общей обойме (рис. 12.12). Одна обойма закреп­лена неподвижно, а другая движется. Сила , приложенная к концу нити, является движущей силой, а вес поднимаемого груза - силой сопротивления. Определим зависимость между силами и с помощью прин­ципа возможных перемещений. Сообщим системе возможное переме­щение, совпадающее с ее истинным перемещением при подъеме груза. Если точка приложения силы получит перемещение , то каждая из шести частей нити между блоками уменьшится на . Поэтому точка при­ложения силы переместится вверх на . Составим уравнение работ в виде (12.5):

,

или

.

Поделив уравнение на , найдем

,

т.е. движущая сила меньше веса поднимаемого груза во столько раз, сколько блоков имеет полиспаст.

Клиновый пресс. Установим зависимость между дви­жущей силой , приложенной к клину, и силой сопро­тивления сжимаемого тела с помощью принципа возможных перемещений. Для этого сообщим систе­ме возможное перемещение, указанное пунктиром на рис. 12.12, и составим уравнение работ в виде (12.5):

.

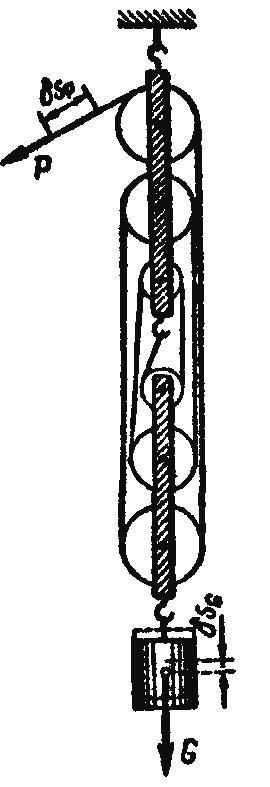
Рис. 12.12

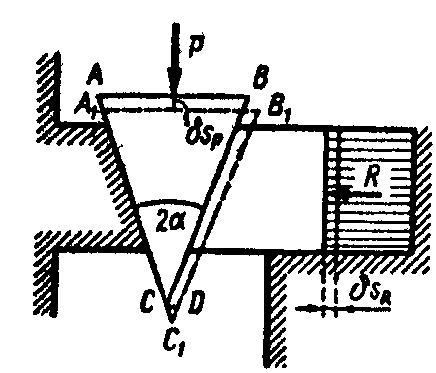
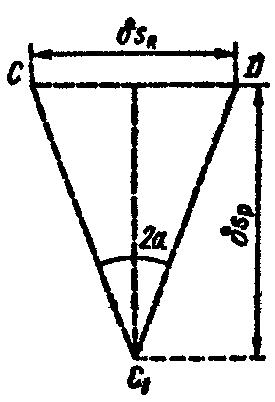
Рис. 12.13 Рис. 12.14

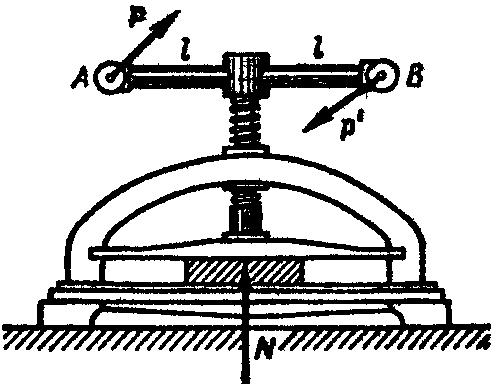
Рис. 12.15

Зависимость между возможными перемещениями то-чек приложения сил и установим из треугольника перемещений CC₁D (рис. 12.14):

.

Подставим это значение в уравнение работ (12.5):

.

Разделим уравнение на :

.

Винтовой пресс. На рис. 12.15 изображена схема винтового пресса. Давление пресса на тело возникает под действием пары сил ( ), приложенной к его рукоятке. Установим зависимость реакции сжимаемого тела от момента приложенной пары сил, пользуясь принципом возможных перемещений, Сообщим частям пресса возможные перемещения, совпадающие с их истинными перемещениями при работе пресса. Повернем рукоятку АВ на малый угол в сторону действия пары сил. Тогда точка прило­жения силы получит возможное перемещение , направление ко­торого противоположно направлению силы . Составим уравнение работ в виде (12.5). Работу пары сил определим по формуле как произведение ее момента на приращение угла поворота тела:

,

где момент пары М == 2Р1.

При одном обороте рукоятки винт перемещается вдоль оси на величину h, называемую шагом винта. Для определения зависимости между и воспользуемся тем, что продольное перемещение винта составляет такую же часть шага винта h, какую угловое перемещение составляет от угла 2π, т. е.

,

откуда

.

Подставим это значение в уравнение работ (12.5):

.

Разделим уравнение на :

.

Сила, сжимающая тело, равна найденной реакции N.

Стержневой пресс. Найдем соотношение между движущими силами и , приложенными к вершинам А и В ромбического четырехзвенника, и силой сопротивления , приложенной в точке D пресса, если =- ; длины стержней пресса указаны на рис. 12.16. Для установления этой зависимости воспользуемся уравнением работ вида (12.7), которое для сил, параллельных оси у, будет иметь вид

. (а)

Проекции сил , и на ось у имеют вид

.

Координаты точек приложения этих сил по оси у

.

Проекции возможных перемещений этих точек на ось у находим, дифференцируя выражения, определяющие координаты этих точек:

Подставляем найденные значения в уравнение (а):

откуда

. (б)

Для установления зависимости между элементарными прираще­ниями углов α и β воспользуемся уравнением, характеризующим связь:

.

Дифференцируем это выражение:

откуда

.

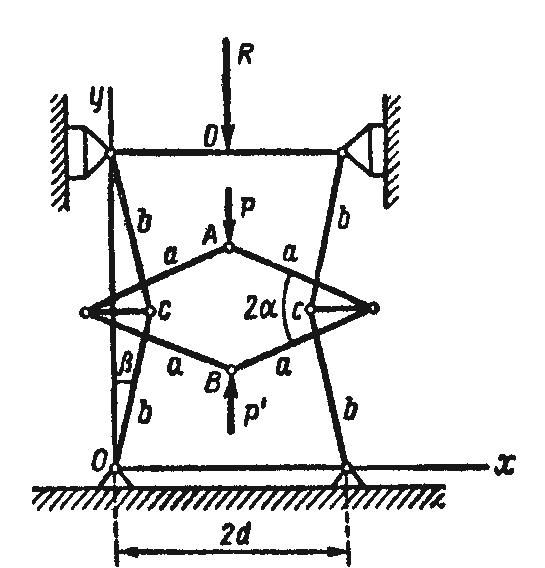
Рис. 12.16

Подставляем это значение в выра­жение (б):

,

отсюда получаем зависимость между величинами сил R и Р в виде

.

Пример применения принципа возможных перемещений к определению реакции связей. В статике обычно приходится определять реакции связей, дей­ствующие на систему, не обладающую ни одной степенью свободы. Такой системой является каждое сооружение, несущее нагрузку, так как оно должно быть неизменяемым и неподвижно прикрепленным к земле.

В этом случае принцип освобождаемости от связей используют следующим образом.

Отбрасывают ту связь, реакцию которой требуется определить. Действие связи заменяют ее реакцией, которая переходит к числе задаваемых сил. При этом система, освобожденная от одной связи (если она статически определима), получает одну степень свободы. Системе сообщают возможное перемещение, соответствующее этой степени свободы.

Составляют уравнение работ в виде (12.5) или (12.7), в которое входят не только задаваемые силы, но и реакция отброшенной связи. Из этого уравнения сразу определяют искомую реакцию.

Для определения реакций других связей поступают так же, отбра­сывая снова только одну связь, т. е. сообщая системе одну степень свободы.

Пример. Конструкция, образованная стержнями, соединенными на концах шарнирами, удерживается в указанном на рис. 12.17, а положении нитью AВ. Найти натяжение нити, вызываемое грузом G, подвешенным в точке D.

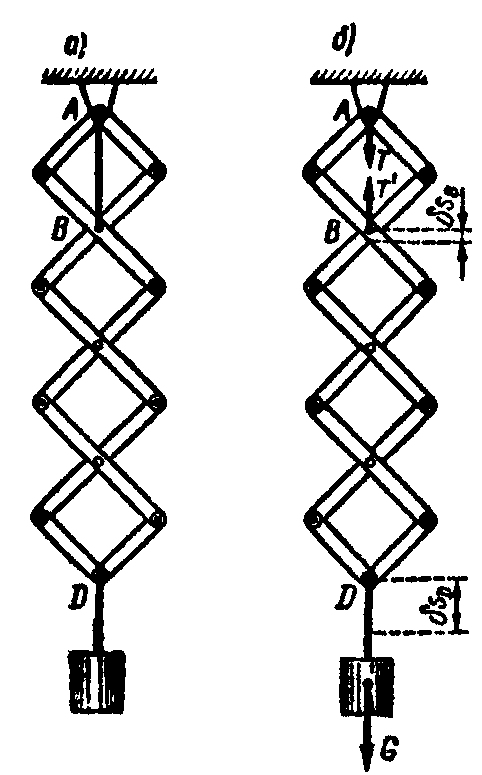
Рис. 12.17

Решение. Чтобы определить натяжение нити АВ, мысленно отбросим эту связь, заменив ее действие на рассматриваемую систему реакциями и , приложенными в точках A и B (рис. 12.17,б). После отбрасывания связи система получит одну степень свободы. Сообщим этой системе возможное перемещение, переместив точку D вниз по вертикали. Тогда вертикальные диагонали образованных стержнями ромбов удлинятся на одну и ту же величину . Возможные перемещения точек А, В, D будут

.

Составим уравнение работ в виде (12.5):

,

И отсюда найдем реакцию нити, равную ее натя­жению:

.

Пример. Балка, состоящая из двух брусьев, соединенных шарниром С, несет нагрузку Р (рис. 12.18, а). Размеры балки и расположение опор показаны на чертеже. Определить силу давления на опору В, вызываемую заданной нагрузкой.

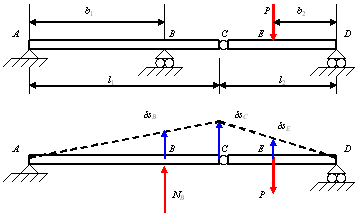
Рис. 12.18

Решение. Отбрасываем опору В и заменяем ее реакцией , численно равной искомой силе давления (рис. 12.18, б). Сообщив системе возможное пере­мещение (у нее теперь появилась одна степень свободы), составляем условие

.

Связь между и находим из пропорций:

, откуда .

Следовательно,

.

При применении метода геометрической статики решение оказалось вы более длинным (пришлось бы рассмотреть равновесие частей балки и ввести дополни­тельно реакции других связей, а затем исключить эти реакции из полученной системы уравнений равновесия).

Лекция 13

ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ

1. Принцип возможных перемещений в случае

движения СИСтемы. Общее уравнение Динамики

Принцип возможных перемещений дает общий метод решения задач статики. С другой стороны, принцип Даламбера позволяет использовать методы статики для решения задач динамики. Сле­довательно, применяя эти два принципа одновременно, мы можем получить общий метод решения задач динамики.

На основании принципа Германа - Эйлера - Даламбера для несвобод­ной механической системы в любой момент временя геометрическая сумма равнодействующей задаваемых сил, равнодей­ствующей реакций связей и силы инерции для каждой точки M_i механической системы равна нулю:

.

Если система получает возможное перемещение, при котором каж­дая точка имеет возможное перемещение (рис. 13.1), то сумма работ этих сил на перемещении должна быть равна нулю:

. (13.1)

Суммируем все n уравнений (13.1):

. (13.2)

Положим, что все связи в рассматриваемой механической системе двусторонние и идеальные (силы тре­ния, если они имеются, отнесены к числу задаваемых сил). Тогда сум­ма работ реакций связей на воз­можных перемещениях системы равна нулю:

При этом условии уравнение (13.2) имеет вид

,

или

. (13.3)

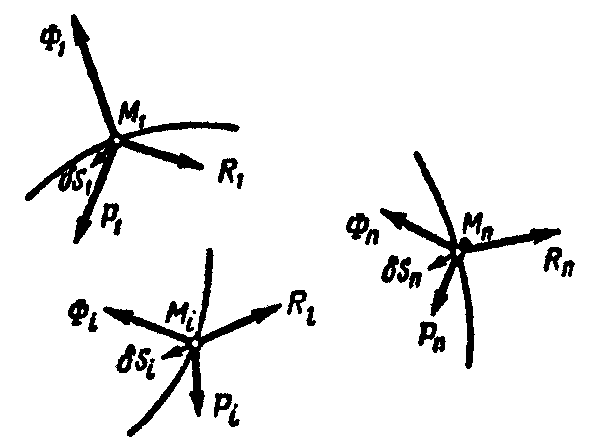
Рис. 13.1

Уравнение (13.3), называемое общим уравнением динамики, показывает, что в любой момент времени сумма работ всех задаваемой сил и сил инерции материальных точек несвободной механической системы с двусторонними идеальными связями на любом возможном ее перемещении равна нулю.

Если в каждую точку М_i системы из некоторого центра О провести вектор , то возможное перемещение этой точки будет соответствующим приращением радиуса-вектора точки:

.

Так как возможное перемещение точки не обязательно направлено в сторону ее действительного движения, то возможное приращение радиуса-вектора не всегда равно действительному приращению, радиуса-вектора точки .

Работу задаваемых и сил инерции на возможных пере­мещениях точек системы можно представить в виде скалярных произведений. Тогда уравнение (13.3) примет вид

,

или

. (13.4)

Обозначим: X_i, Y_i, Z_i проекции задаваемых сил на неподвижные оси декартовых координат, Ф_ix, Ф_iy, Ф_iz - проекции сил инерции , а δx_i, δy_i, δz_i - проекции векторов возможных перемещений на те же оси.

Пользуясь аналитическим выражением элементарной работы, уравнению (13.4) можно придать следующий вид:

. (13.5)

Выразим проекции силы инерции точки на оси координат через проекции ее ускорения:

Подставив эти значения в уравнение (13.5), окончательно получим:

. (13.6)

Общее уравнение динамики (13.6) позволяет составить дифферен­циальные уравнения движения любой механической системы. Если ме­ханическая система состоит из отдельных твердых тел, то силы инерции точек каждого тела можно привести к силе, приложенной в некоторой точке тела, и паре сил. Сила равна главному вектору сил инерции точек этого тела, а момент пары равен главному моменту этих сил относительно центра приведения. Чтобы воспользоваться принципом возможных перемещений, к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силу и пару, составленные силами инерции точек тела. Затем системе сообщают возможное перемеще­ние и для всей совокупности задаваемых сил и приведенных сил инерции составляют уравнение (13.3) или (13.6). Если среди связей системы имеются односторонние, то для приме­нения общего уравнения динамики необходимо, чтобы возможные перемещения системы не были освобождающими.