2. Принцип возможных перемещений

При решении задач статики для определения реакций связей исполь­зовались уравнения равновесия твердого тела. При этом реакции свя­зей не выделялись из общего числа приложенных к телу сил. В слож­ных несвободных механических системах определение реакций связей с помощью уравнений равновесия становится громоздким и потому малопригодным. В этих случаях целесообразно использовать принцип возможных перемещений, который формулируется так: необходимое и достаточное условие равновесия системы сил, приложенных к меха­нической системе, подчиненной стационарным двусторонним и идеаль­ным связям, заключается в равенстве нулю суммы элементарных работ задаваемых сил на любом возможном перемещении системы из рассматриваемого ее положения.

Чтобы доказать необходимость принципа, предположим, что несво­бодная механическая система, подчиненная стационарным двусторонним и идеальным связям, находится под действием уравновешивающихся сил. Тогда силы, действующие на каждую точку системы, должны также уравновешиваться, т. е.

или

,

где — равнодействующая задаваемых сил, приложенных к i-й точке системы; - равнодействующая реакций связей, приложенных к той же точке.

Мысленно сообщим рассматриваемой системе возможное переме­щение из занимаемого ею положения. Обозначим возможные перемещения точек системы . (рис. 12.11). Вычислим сумму работ сил, приложенных к каждой из точек системы, при возможном перемещении этой точки. Так как силы и равны и противоположны по направлению, то и работы этих сил на перемещении , равны по величине, но противоположны по знаку. Поэтому сумма работ этих сил равна нулю:

.

Просуммируем все n уравнений, составленных для сил, приложен­ных к каждой точке системы:

. (12.4)

Предположим, что в рассматриваемой механической системе все связи являются стационарными, дву­сторонними и идеальными, а силы трения, если они имеются, отнесем к задаваемым силам. Тогда сумма работ реакций связей на возможных перемещениях должна быть равна нулю

.

При этом условии уравнение (12.4) примет вид

(12.5)

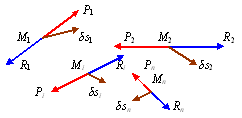
Рис. 12.11

Таким образом, необходимость принципа доказана.

Для доказательства достаточности принципа, т.е. существования равновесия сил при выполнении условий (12.5), рассуждение проведем от обратного. Предположим, что условие (12.5) выполнено, но силы, приложен­ные к системе, не уравновешиваются. В этом случае, если в началь­ный момент система находилась в покое, под действием не уравнове­шивающихся задаваемых сил и реакций связей она придет в движение и за малый промежуток времени совершит некоторое действительное перемещение, которое в случае стационарных связей будет возможным перемещением. Так как перемещение отдельных точек системы из состояния покоя произойдет в направлении равнодействующих сил и , то при этом будет совершена положительная работа

.

Вторая сумма равна нулю, так как по условию связи системы идеальны. Следовательно,

,

что противоречит принятому предположению (12.5), т.е. доказана достаточность принципа. При односторонних связях уравнение (12.5) остается справедливым лишь в том случае, когда возможные перемещения являются неосвобождающими. В общем же случае при односторонних связях . Если в каждую точку М_i системы из некоторого центра О про­вести вектор , то возможное перемещение этой точки будет соответствующим возможным приращением радиуса-вектора точки:

.

Тогда уравнение работ (12.5) примет вид

. (12.6)

Обозначим проекции задаваемой силы на неподвижные оси де­картовых координат Х_i,Y_i, Z_i, а проекции возможного перемещения на те же оси — . Пользуясь аналитическим выражением элементарной работы, представим уравнение работ (12.5) в сле­дующем виде:

. (12.7)

Если система, состоящая из большого числа тел, имеет одну сте­пень свободы, то одно из равенств (12.5), (12.6) или (12.7) устанав­ливает сразу условие равновесия задаваемых сил, приложенных к сис­теме. Если эта система имеет несколько степеней свободы, то урав­нения работ составляются для каждого независимого перемещения системы в отдельности. Таким образом, получается столько условий равновесия системы, сколько степеней свободы она имеет. Рассмотрим одно из преобразований уравнения работ (12.5), при­менение которого к решению некоторых задач является полезным. Предположим, что смещение механической системы из состояния покоя происходит в течение ничтожно малого промежутка времени τ, и определим скорости, с которыми будут перемещаться точки системы:

.

Эти скорости назовем возможными скоростями точек системы.

Направления векторов этих скоростей совпадают с направлениями возможных перемещений . Разделив уравнение работ (12.5) на величину τ, получим

.

Учитывая, что , а направление совпадает с направлением , будем иметь

. (12.8)

Уравнение (12.8) эквивалентно уравнению (12.5), но является не уравнением работ, а уравнением мощностей.