4. Определение динамических реакций подшипников при вращения твердого тела вокруг неподвижной оси

Рассмотрим твердое тело, вращающееся вокруг неподвижной оси z под действием приложенных к нему внешних задаваемых сил (рис. 11.5, а). Предположим, что в рассматриваемый момент тело имеет угловую скорость ω и угловое ускорение ε. Чтобы воспользоваться принципом Германа - Эйлера - Даламбера, приложим к каждой точке тела М_i силу инерции . При неравномерном вращении тела эта сила состоит из вращатель­ной силы инерции , направленной противоположно вращательному ускорению точки М_i и центробежной силы инерции , направленной противоположно центростремительному ускорению этой точки. Приме­няя принцип освобождаемости от связей, заменяем действие на тело подпятника А и подшипника В реакциями и , разложив их на составляющие . Расстояние АВ между опорами тела обозначим h. На основании принципа Германа - Эйлера - Даламбера внешние задаваемые силы, реакции связей и силы инерции должны удовлетворять уравнениям (11.4) и (11.6), которые в данном случае принимают вид

. (11.14)

но .

Первому уравнению (11.14) соответствуют три уравнения проекций внешних задаваемых сил, реакций связей и сил инерции на оси коор­динат. Второму уравнению (11.14) соответствуют три уравнения момен­тов этих же сил относительно осей координат. Таким образом, всею имеем шесть следующих уравнений:

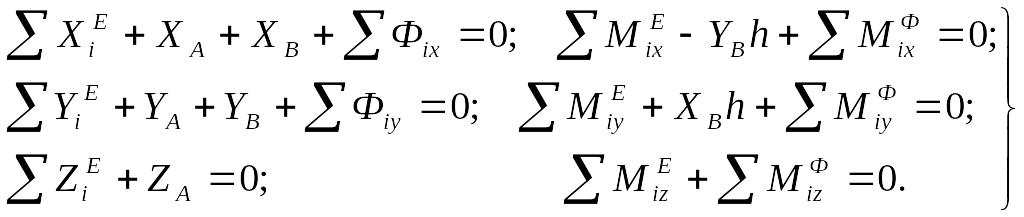(11.15)

Установим формулы для вычисления сумм проекций сил инерции на оси координат и их моментов относительно этих осей. Модули центробежной и вращательной сил инерции определим по формулам:

,

где — радиус окружности, описываемой точкой.

Разложим каждую из этих сил на составляющие, направленные по осям координат (рис. 5, б). Найдем алгебраические значения этих составляющих, т. е. проекции сил и на оси координат:

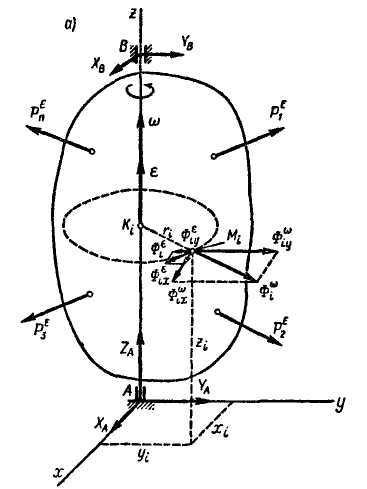
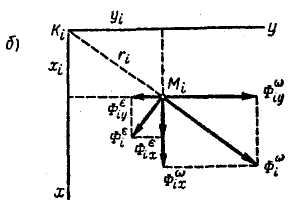
Рис. 11.5

Найдем суммы проекций сил инерции на оси х и у, пользуясь равенствами , полученными из формул:

Найдем суммы моментов сил инерции относительно осей х и у как суммы моментов центробежных и вращательных сил инерции:

где и центробежные моменты инерции тела относительно осей у, z и осей z, х:

Учитывая, что центробежные силы инерции пересекают ось z, най­дем сумму моментов сил инерции относительно оси z как сумму моментов только вращательных сил инерции, не разложенных на составляющие:

Подставим найденные значения в уравнения (15):

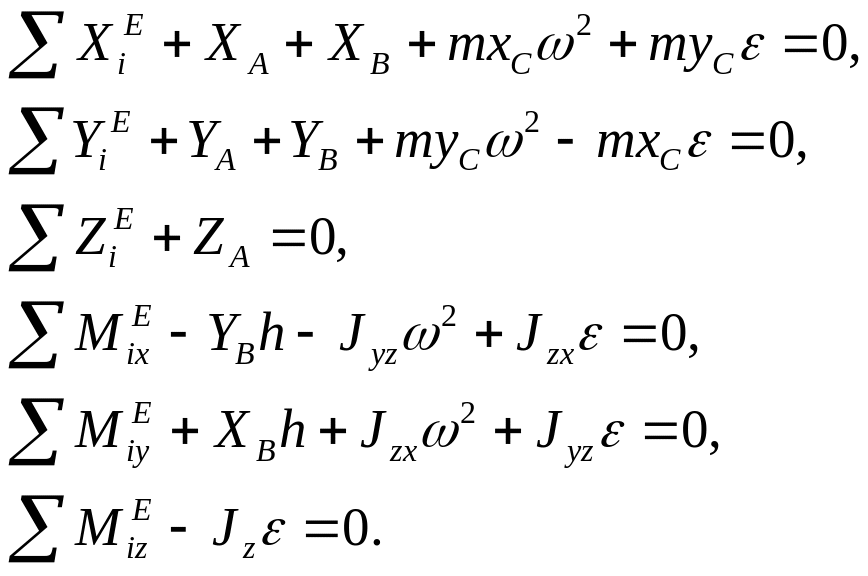(11.16)

Последнее из уравнений (11.16) не содержит реакций опор. Это уравнение представляет собой дифференциальное уравнение вращения тела. Остальные пять уравнений позволяют определить пять составляющих реакций подпятника А и подшипника В. В первое, второе, четвертое и пятое уравнения (11.16), из которых определяются составляющие реакций опор вдоль осей х и у, входят члены, зависящие как от внешних задаваемых сил, так и от сил инер­ции. Следовательно, каждая из этих реакций имеет статическую состав­ляющую, вызываемую действием внешних задаваемых сил , и дина­мическую составляющую, зависящую от сил инерции. Члены уравне­ний (11.16), зависящие от сил инерции, отмечены рамками. При быст­ром вращении тела динамические составляющие могут иметь большие значения. Установим условия, при которых динамические составляющие реакций подпятника и подшипника равны нулю. Чтобы получить эти условия, приравняем нулю сумму членов, зависящих от сил инерции, в каждом из уравнений (11.16):

, (11.17)

(11.18)

Решаем систему уравнений (11.17) относительно х_С и у_С:

,

т. е. устанавливаем, что центр тяжести тела должен находиться на оси его вращения. Решаем систему уравнений (18) относительно J_yz и J_zx:

.

Это означает, что ось вращения тела z должна быть главном осью инерции тела для начала координат.

Таким образом, установлено, что динамические составляющие реак­ций подпятника и подшипника равны нулю в том случае, если ось вращения тела является главной центральной осью инерции тела.

Для выполнения этого условия вращающимся частям машин обычно придают форму тел вращения с тем, чтобы это тело вращалось вокруг своей оси симметрии. Если из-за неточности изготовления ось вращения тела не окажется главной центральной осью инерции, то эта погрешность устраняется специальными приемами.

Лекция 12

ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ

1. Возможные перемещения

механической системы. Идеальные связи

Обобщенные координаты и число степеней свободы

Перемещения точек несвободной механической системы не могут быть совершенно произвольными, так как они ограничены имеющи­мися связями. Это означает, что не все координаты точек независимы. При таком условии положение точек системы определяется заданием только независимых координат. Остальные координаты опре­деляются из уравнений связей. Независимые величины, заданием которых однозначно определяется положение всех точек механической системы, называются обобщенны­ми координатами этой системы. Для голономных систем число неза­висимых обобщенных координат механической системы равно числу степеней свободы этой системы. Так, например, положение рычага АВ с осью вращения О (рис. 12.1) вполне определяется заданием его угла поворота φ. Угол φ можно рассматривать как обобщенную координату рычага. Так как положение рычага определяется одной обобщенной координатой, то рычаг имеет одну степень свободы. Положение всех точек кривошипного механизма (рис. 12.2) вполне определяется заданием только угла поворота кривошипа φ. Этот угол можно принять за обобщенную координату этой системы, имеющую также одну степень свободы.

Положение всех точек центробежного регулятора (рис. 12.3), вращаю­щегося вокруг вертикальной оси, определяется заданием угла пово­рота регулятора φ и угла а, образованного каждым из стержней с вертикалью. Не зависящие друг от друга углы φ и а можно считать обобщенными координатами. Так как положение регулятора определя­ется двумя обобщенными координатами, то он имеет две степени свободы.

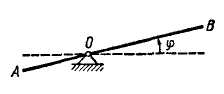
Рис. 12.1 Рис. 12.2

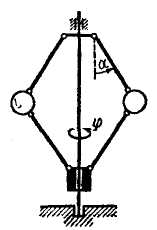
Рис. 12.3

Положение свободной материальной точки в пространстве опреде­ляется тремя декартовыми координатами, не зависимыми друг от друга. Поэтому свободная материальная точка имеет три степени свободы. Твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы, так как его положение определяется только углом поворота φ. Тело, совершающее сферическое движение, имеет три степени сво­боды, так как его положение определяется тремя эйлеровыми углами: ψ,θ,φ. Свободное твердое тело, движение которого определяется шестью уравнениями, имеет шесть степеней свободы. Механическая система, положение которой определяют s обобщенных координат, имеет s степеней свободы.

Декартовы координаты любой точки M_i механической системы являются функциями обобщенных координат этой системы. Так, на­пример, зная длину кривошипа r и длину шатуна l кривошипно-шатунного механизма (рис. 12.4), можно выразить декартову коорди­нату ползуна В через обобщенную координату φ:

, или .

Таким же образом, можно определить координату любой точки этого механизма. Обозначим q₁, q₂, ..., q_s обобщенные координаты механической системы, имеющие s степеней свободы. Декартовы координаты любой точки М_i этой системы при стацио­нарных связях являются функциями s обобщенных координат:

(12.1)

При наличии нестационарных связей декартовы координаты всех точек механической системы являются функциями не только обобщенных координат, но и времени:

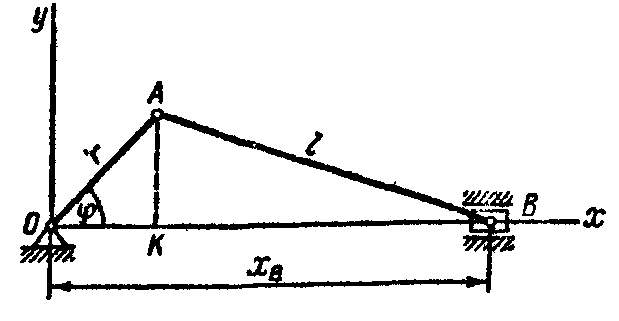
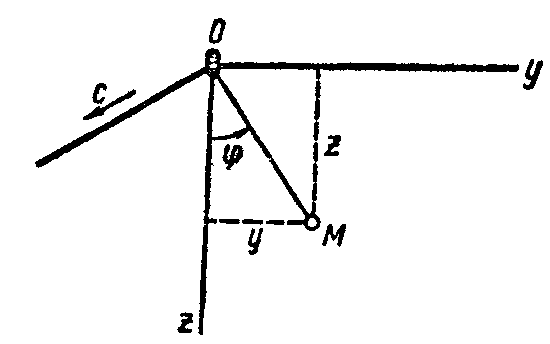
Рис. 12.4 Рис. 12.5

(12.2)

Например, при переменной длине нити маятника ОМ =l = l_о - сt (рис. 12.5) точка М имеет координаты

.

Эти координаты зависят не только от обобщенной координаты φ, но и от временя t.