2. Дифференциальные уравнения движения материальной точки

В декартовых координатах. Рассмотрим движение материальной точки М массой т под действием приложенных к ней сил (рис. 1.6). Выберем прямоугольную систему осей координат х, у, z. Основное уравнение динамики имеет вид

. (1.11)

Проецируем обе части векторного равенства (1.11) на координатные оси:

(a)

где X₁, Y₁, Z₁; X₂, Y₂, Z₂; ... ; X_n,У_n, Z_n - проекции сил на оси х, у, z.

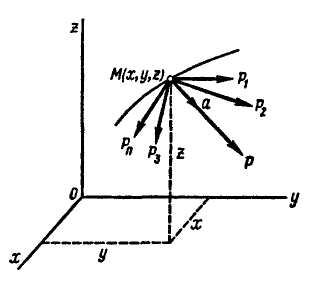
Рис. 1.6

Из кинематики известно, что проекция ускорения точки на каждую ось декартовых координат равна второй производной по времени от соответствующей координаты точки, т. е.

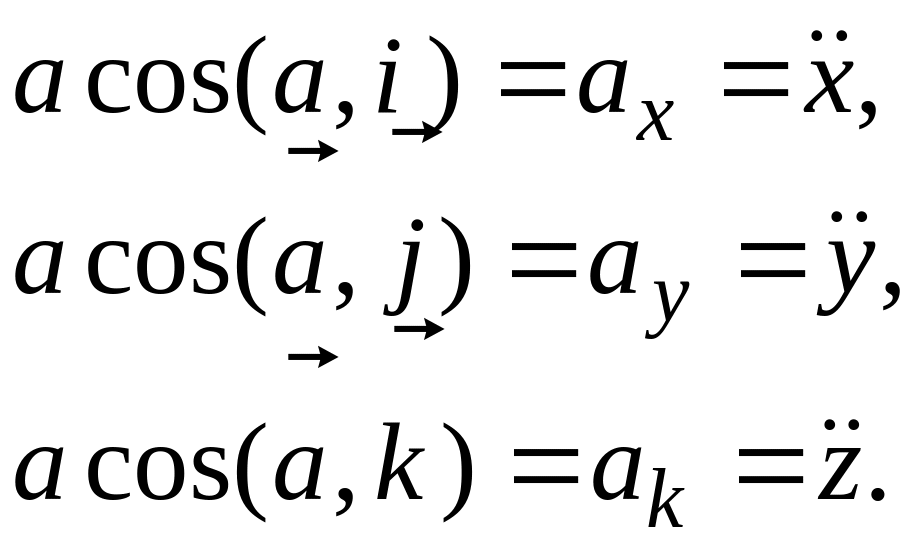
Подставляем эти значения в равенства (а):

(1.12)

Уравнения (1.12) называются дифференциальными уравнениями движения материальной точки.

Естественные уравнения движения материальной точки. Спроецируем обе части векторного равенства (1.11) на естественные координатные оси (подвижные) - касательную, главную нормаль и бинормаль (рис. 1.7):

(a)

Проекции ускорения на касательную и главную нормаль определяются по формулам из кинетики:

Подставляем значения этих проекций в два первых равенства (а):

(1.13)

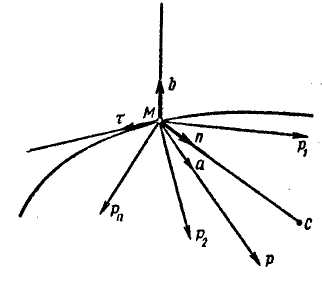
Рис. 1.7

Из кинематики известно, что вектор ускорения лежит в соприкасающейся плоскости и его проекция на бинормаль равна нулю:

Из третьего равенства (а) следует, что сумма проекций всех сил, приложенных к точке, на бинормаль равна нулю:

Уравнения (1.13) называются естественными уравнениями движения материальной точки. Этими уравнениями удобно пользоваться в том случае, когда известна траектория точки.

3 Первая основная задача динамики

С помощью дифференциальных уравнений движения точки можно решать две основные задачи динамики точки.

Первая задача динамики. Зная массу точки т и уравнения ее движения , найти модуль и направление равнодействующей сил, приложенных к точке. Эта задача легко решается следующим путем:

Рис. 1.8

Пример. Уравнения движения точки М массой m имеют вид

.

Определить равнодействующую приложенных к точке сил.

Решение. Исключая время t из уравнений движения, находим уравнение траектории точки:

Траектория - окружность радиусом r (рис. 1.8).

Определяем проекции ускорения точки на оси координат:

.

Находим проекции равнодействующей силы:

Определяем модуль и направление силы:

Углы, составленные направлением силы с направлением осей координат, имеют значения

т. е. в любой момент сила направлена к началу координат О.

Лекция 2

ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ

1. Содержание задачи. Начальные и конечные

условия движения

Вторая задача динамики - Зная силы, действующие на материальную точку, ее массу т, а также начальное положение точка и ее начальную скорость, определить закон движения точки:

.

Дифференциальные уравнения движения материальной точки имеют вид:

(2.1)

Для решения этой задачи необходимо в левую часть уравнений (2.1) подставить значение массы m, а в правую часть - суммы проекций приложенных сил и полученные уравнения дважды проинтегрировать по времени (рис. 2.1). Эта задача имеет большое практическое значение и в общем случае является более сложной, чем первая.

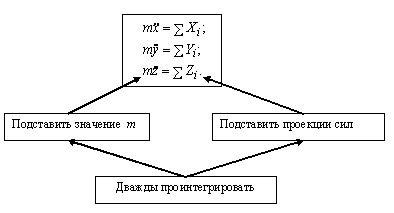
Рис. 2.1

Решение задач динамики точки путем интегрирования соответ­ствующих дифференциальных уравнений движений сводится к следующим операциям.

1. Составление дифференциального урав­нения движения. Для его составления в случае прямоли­нейного движения надо:

а) выбрать начало отсчета (как правило, совмещая его с начальным положением точки) и провести координатную ось, направляя ее вдоль траектории и, как правило, в сторону движения; если под действием приложенных сил точка может находиться в каком-нибудь, положении в равновесии, то начало отсчета удобно помещать в положении статического равновесия;

б) изобразить движущуюся точку в произвольном положении (но так, чтобы было и ; последнее существенно, когда среди сил есть силы, зависящие от скорости) и показать все действующие на точку силы;

в) подсчитать сумму проекций всех сил на координатную ось и подставить эту сумму в правую часть дифференциального уравне­ния движения; при этом надо обязательно все переменные силы вы разить через те величины (t, х или v), от которых эти силы зависят.

2. Интегрирование дифференциального уравнения движения. Интегрирование производится методами, известными из курса высшей математики и зависящими от вида полученного уравнения, т. е. от вида его правой части. В тех случаях, когда на точку кроме постоянных сил действует одна переменная сила, зависящая только от времени t или только от расстояния х, или же только от скорости v, уравнение прямолинейного движения можно проинтегрировать методом разделения переменных. Если при этом в задаче требуется определить только скорость, то часто можно при решении ограничиться интегрированием одного из уравнений (2.1).

3. Определение постоянных интегрирования. Для определения постоянных интегрирования надо данным задачи установить начальные условия. При этом постоянные можно определять непосредственно после каждого интегрирования.

Если дифференциальное уравнение движения является уравнением с разделяющимися переменными, то вместо введения постоянных интегрирования можно брать сразу от обеих частей равенства определенные интегралы в соответствующих пределах.

4. Нахождение искомых в задаче величин исследование полученных результатов. Чтобы иметь возможность исследовать решение, а также произвести косвенную проверку результата подсчетом размерностей, надо решение проводить до конца в общем виде (в буквах), подставляя числовые данные только в окончательные результаты.

Сделанные здесь указания относятся и к случаю криволинейного движения.

Taк как силы, действующие на материальную точку, в общем случае являются переменными величинами, то правые части дифференциальных уравнений движения могут быть функциями f,х,у,z, , а потому система дифференциальных уравнений (2.1) в общем случае будет совместной.

При интегрировании каждого дифференциального уравнения движения точки появляются две постоянные, а потому при интегрировании трех дифференциальных уравнений движения точки будет шесть постоянных. Значения этих постоянных определяют по начальным условиям движения: значениям трех координат точки и проекций eе скорости на три оси в некоторый момент времени, обычно (но не обязательно) в начальный момент.

Пусть в начальный момент времени известны координаты точки и проекции ее скорости на оси, т. е.

Эти значения подставляют в уравнения, представляющие собой общие решения дифференциальных уравнений движения точки.

Из этих уравнений определяют постоянные интегрирования в зависимости от начальных координат и проекций начальной скорости. Подставляя найденные значения постоянных интегрирования в общее решение дифференциальных уравнений движения точки, получают уравнения движения точки в виде

(2.2)

Уравнения (2.2) показывают, что под действием одной и той же силы материальная точка может совершать целый класс движений. определяемых начальными условиями движения.

Так, например, под действием силы тяжести материальная точка может двигаться как по вертикали, так и по семейству парабол, причем вид траектории ее движения будет зависеть от начальных условий ее движения.

Действительно, координаты движущейся точки в каждый момент зависят как от действующих на точку сил, так и от начального положения точки и ее начальной скорости.

При составлении дифференциальных уравнений движения материальной точки за расчетный начальный момент обычно принимается момент начала движения материальной точки под действием заданных сил, для которого известны как положение точки, так и ее скорость.

Путем введения начальной скорости точки учитывается влияние на ее движение сил, действовавших на материальную точку до того момента, который принят за начальный.

Так, например, скорость вылета снаряда из орудия, принимаемая за начальную скорость его полета, учитывает результат действия на снаряд сил давления пороховых газов при движении снаряда по каналу стола орудия до момента его вылета из орудия.

Дифференциальные уравнения движения материальной точки описывают движение точки до тех пор, пока на нее действуют силы, вошедшие в правую часть уравнений (2.1). Если в какой-то момент времени действие этих сил на материальную точку изменяется или прекращается, то для описания последующего движения точки надо составлять новые дифференциальные уравнения ее движения. Начальными условиями нового движения точки будут ее положение и скорость в конце предшествующего движения.

Процесс интегрирования дифференциальных уравнений движения точки разберем на конкретных примерах. При этом рассмотрим следующие случаи изменения силы, действующей на точку:

1) сила постоянна по модулю и направлению;

2) сила зависит от времени;

3) сила зависит от скорости точки.

3) сила зависит от положения точки в пространстве;