2. Принцип Германа - Эйлера - Даламбера для несвободной механической системы

При изучении движения несвободной механической системы, так же как и при изучении движения одной несвободной точки, применяют принцип освобождаемости от связей. По этому принципу имеющиеся связи отбрасывают, заменяя их действие соответствующими реакциями. Полученную механическую систему рассматривают как сво­бодную, находящуюся под действием задаваемых сил и реакций свя­зей. Рассмотрим несвободную механическую систему, состоящую из n материальных точек. Применим к каждой точке M_i этой системы принцип Германа - Эйлера - Даламбера. Тогда

, (11.2)

где — равнодействующая задаваемых сил, приложенных к точке M_i;

- равнодействующая реакций связей, приложенных к этой точке;

- сила инерции материальной точки M_i.

Уравнение (11.2) показывает, что в любой момент времени гео­метрическая сумма равнодействующей задаваемых сил, равнодействую­щей реакции связей и силы инерции для каждой материальной точки несвободной механической системы равна нулю.

Это положение называется принципом Германа—Эйлера—Далам­бера для несвободной механической системы.

Сложим все п уравнений (11.2):

. (11.3)

Здесь - главный вектор задаваемых сил; - главный вектор реакций связей; — главный вектор сил инер­ции точек системы.

Подставляем эти значения в уравнение (11.3):

. (11.4)

Из уравнения (11.4) следует, что в любой момент времени для всякой несвободной механической системы геометрическая сумма глав­ных векторов задаваемых сил, реакций связей и сил инерции материаль­ных точек системы равна нулю.

Проведем из произвольного неподвижного центра О в каждую точку системы М_i радиусы-векторы . Умножим векторно радиус-вектор каждой точки на сумму векторов левой части равенств (11.2):

.

Сложим все n полученных уравнений:

. (11.5)

Здесь - главный момент задаваемых сил относительно центра О; - главный момент реакций связей относительно центра 0; - главный момент сил инерции точек системы относительно центра О. Подставляя эти значения в уравнение (11.5), получаем

. (11.6)

Уравнение (11.6) показывает, что в любой момент времени для всякой несвободной механической системы геометрическая сумма главных моментов задаваемых сил, реакций связей и сил инерции мате­риальных точек системы относительно любого неподвижного центра равна нулю.

3. Приведение сил инерции точек твердого тела к простейшему виду

К системе сил инерции точек твердого тела можно применить метод Пуансо — метод приведения сил к некоторому центру, рассмот­ренный в статике. В динамике за центр приведения сил инерции выбирают обычно центр масс тела С. Тогда в результате приведения получится сила , равная главному вектору сил инерции точек тела, и пара сил с моментом , равным главному моменту сил инерции относительно центра масс:

(11.7)

, (11.8)

где радиусы-векторы проведены во все точки тела из центра масс.

Количество движения системы

.

Продифференцируем это выражение по времени:

.

Пользуясь этим выражением, получим главный вектор сил инерции точек твердого тела при любом его движе­нии:

. (11.9)

Остается определить главный момент сил инерции точек тела от­носительно центра масс. Рассмотрим некоторые случаи движения твердого тела.

Поступательное движение. В случае поступательного движения ускорения всех точек тела геометрически равны ускорению его центра масс. При этом условии

,

так как радиус-вектор центра масс относительно центра масс равен нулю. В этом случае силы инерции точек твердого тела приводятся к равнодействующей, приложенной в центре масс и равной главному вектору сил инерции, а потому

.

Таким образом, при поступательном движении силы инерции точек твердого тела приводятся к равнодействующей силе, приложенной в центре масс тела, равной по модулю произведению массы тела на модуль ускорения его центра масс и направленной противоположно этому ускорению.

Вращение твердого тела, имеющего плоскость материальной симмет­рии, вокруг неподвижной оси, перпендикулярной этой плоскости. В этом случае неподвижная ось вращения тела является главной осью инер­ции тела в точке О. Каждой точке (рис. 11.2, а) соответствует точка такой же массы, симметричная относительно заданной плоскости (на рис. 2, а эта плоскость заштрихована). Из кинематики известно, что ускорения всех точек, лежащих на одной прямой, параллельной оси вращения, геометрически равны. Поэтому силы инерции и точек и геометрически равны и их равнодействующая приложена в точке , лежащей в плоскости симметрии. Отсюда следует, что в точке приложена равнодействующая сил инерции всех точек тела, лежащих на перпендикуляре к плоскости симметрии, восставленном в этой точке. Таким образом, сложение сил инерции точек тела в этом случае движения сводится к сложению сил инерции точек материальной плоской фигуры, имеющей массу данного тела и тот же момент инерции относительно оси вращения (рис. 11.2, б).

Приведем силы инерции точек фигуры к центру ее вращения О. При приведении получим силу, приложенную в этом центре, и пару сил, лежащую в плоскости фигуры. Сила равна главному вектору, определяемому формулой (11.9):

.

Главный вектор направлен противоположно ускорению центра масс и имеет модуль

.

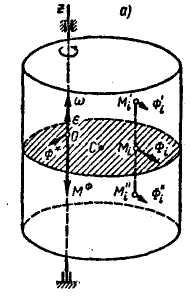
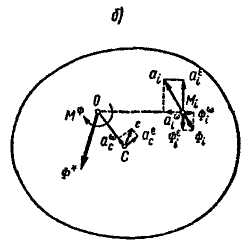
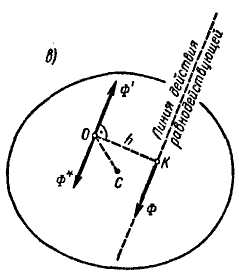
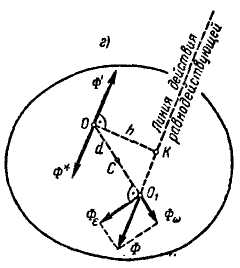
Рис. 11.2

Для определения момента пары разложим силу инерции каждой точки на вращательную и центробежную силы инерции, направленные противоположно вращательному и центростремительному ускорениям этой точки. Их модули определим по формулам

.

Так как линии действия центробежных сил инерции проходят через центр вращения О, то искомый момент пары равен сумме моментов вращательных сил инерции относительно точки О:

.

Здесь — момент инерции материальной плоской фигуры относительно оси Оz, перпендикулярной ее плоскости, равный моменту инерции данного тела относительно этой оси. Таким образом, алгебраическая величина момента пары, составленной силами инерции,

, (11.10)

где J_z — момент инерции тела относительно оси вращения; ε — алгебраическая величина углового ускорения тела. Вектор направлен перпендикулярно плоскости фигуры, т. е. по оси вращения тела противоположно вектору углового ускорения:

.

Как известно из статики, силу и пару с моментом , лежащие в одной плоскости, можно заменить одной равнодействующей силой , геометрически равной главному вектору (рис. 11.2, в). Линия действия этой силы отстоит от центра приведения О на расстоянии

. (11.11)

Таким образом, при вращении твердого тела, имеющего плоскость материальной симметрии, вокруг оси, перпендикулярной этой плоскости, силы инерции точек тела приводятся к равнодействующей силе, лежа­щей в плоскости симметрии. Модуль и направление этой силы опре­деляются формулой (11.9), а расстояние от ее линии действия до точки пересечения оси вращения с плоскостью симметрии — формулой (11.11).

Покажем, что линия действия равнодействующей сил инерции проходит через центр качаний. Для этого продолжим линию действия этой силы до пересечения с прямой ОС; перенесем в точку их пере­сечения O₁ силу и разложим ее на две составляющие: и (рис. 11.2, г). На основании теоремы о моменте равнодействующей силы

. (а)

Так как линия действия проходит через точку О, то

. (б)

Принимая ОС = d, имеем

.

Поэтому на основании (а) и (б)

,

откуда .

Из этого равенства следует, что точка О₁ через которую проходит линия действия равнодействующей сил инер­ции , является центром качаний.

Вращение твердого тела, имеющего плоскость материальной симмет­рии, вокруг центральной оси, перпендикулярной этой плоскости. В этом случае ось вращения тела является главной центральной осью инерции тела, так как она проходит через центр масс тела перпендикулярно плоскости симметрии (рис. 11.3). При неподвижном центре масс тела из формулы (11.9) следует

,

т.е. главный вектор сил инерции точек тела равен нулю.

Из формулы (11.10) получим

, (11.12)

где J_Сz — момент инерции тела относительно оси вращения.

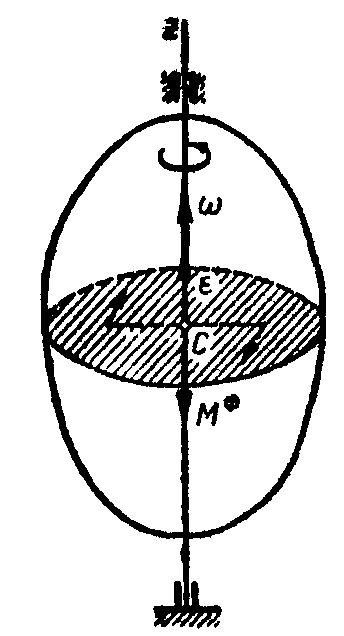
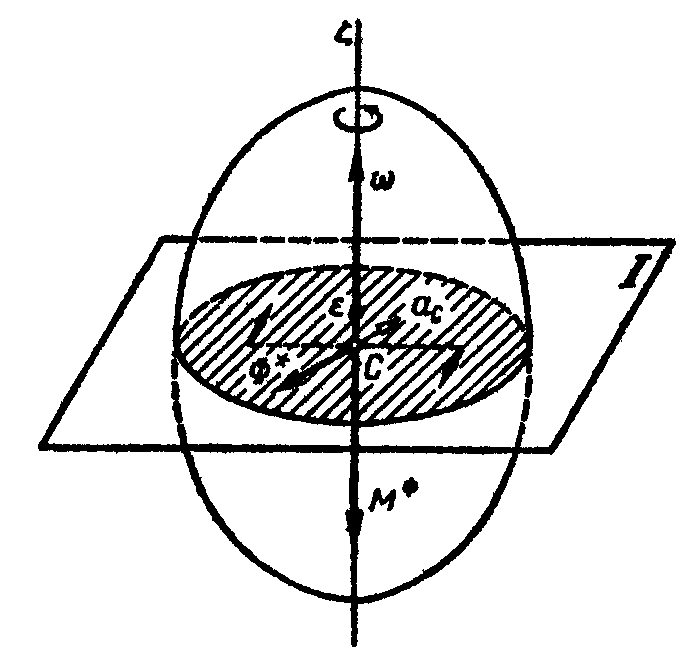
Рис. 11.3 Рис. 11.4

Таким образом, если твердое тело вращается вокруг неподвижной оси, которая является его главной центральной осью инерции, то силы инерции точек тела приводятся к паре сил, лежащей в плоскости материальной симметрии тела, момент которой определяется по фор­муле (11.12).

Плоское движение твердого тела, имеющего плоскость материальной симметрии. Рассмотрим такое движение твердого тела, имеющего плоскость материальной симметрии, при котором все точки тела дви­жутся параллельно этой плоскости (рис. 11.4). Это движение тела можно разложить на поступательное движение с центром масс тела С и вра­щение вокруг подвижной оси Cζ, проходящей через центр масс тела перпендикулярно плоскости симметрии. Как уже известно, силы инерции поступательного движения тела приводятся к силе, приложенной в центре масс и определяемой формулой (11.9):

.

Силы инерции вращательного движения тела в таком случае при­водятся к паре сил, лежащей в плоскости симметрии и имеющей момент

, (11.13)

где J_ζ - момент инерции тела относительно главной центральной оси инерции Сζ.

Таким образом, если твердое тело, имеющее плоскость материаль­ной симметрии, движется параллельно этой плоскости, то силы инер­ции точек тела приводятся к силе, приложенной в центре масс и рав­ной главному вектору сил инерции, и к паре сил, лежащей в плоскости симметрии, числовое значение момента которой определяется формулой (11.13).

В более сложных случаях движения тела главный вектор и главный момент сил инерции относительно центра приведения находят анали­тическим путем, т. е. по их проекциям на три координатные оси.