4. Теорема об изменении кинетической энергии механической системы

Установим зависимость между изменением кинетической энергии механической системы и работой приложенных к ее точкам сил. Для этого разделим силы, действующие на точки , на внешние силы , и внутренние силы . Применим к движению каждой точки M_i теорему об изме­нении кинетической энергии. Предположим, что при перемещении механической системы из первого положения во второе каждая точка M_i перемещается из М_i1 в М_i2, причем скорость ее изменяется от v_i1 до v_i2 (рис. 8).

Тогда по ypавнению (10.3) для каждой материальной точки

,

где - работ силы и - работа силы на перемещении М_i1М_i2.

Просуммируем левые и правые части составленных n равенств:

.

Согласно (10.5), - ки­нетическая энергия системы в первом ее положении; — кинетическая энергия системы во втором положении.

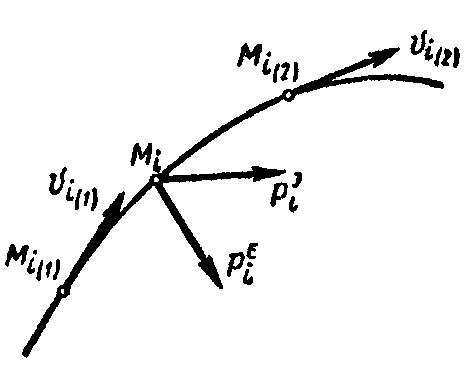
Рис. 10.8

Таким образом,

. (10.14)

Уравнение (10.14) выражает теорему об изменении кинетической энергии механической системы: изменение кинетической энергии меха­нической системы на некотором перемещении равно сумме работ внешних и внутренних cuл, действующих на материальные точки системы на этом перемещении.

Сумма работ внутренних сил твердого тела на любом перемещении равна нулю, т. Е. . Для твердого тела уравнение (14) принимает вид

, (10.15)

т. е. изменение кинетической энергии твердого meла на некотором пере­мещении равно сумме работ внешних сил, действующих на тело на этом перемещении.

Механический коэффициент полезного действия машины

Для установления мощности машины необходимо рассмотреть действующие на машину силы. Эти силы можно разделить на три кате­гории:

1. Силы, совершающие положительную работу, называемые движу­щими силами, например давление пара на поршень в цилиндре паровой машины или газа в двигателе внутреннего сгорания.

2. Силы, совершающие отрицательную работу, называемые силами сопротивления. Силы сопротивления делятся на две группы:

а) полезные силы сопротивления - силы, для преодоления которых предназначена машина, например сопротивление поднимаемого маши­ной груза и т. д.;

б) вредные силы сопротивления - побочные силы сопротивления, как, например, силы трения, сопротивление воздуха и т. п.

3. Силы тяжести отдельных частей машины, совершающих попере­менно то положительную, то отрицательную работу. Работа этих сил за полный цикл работы машины равна нулю, так как результирую­щее перемещение точки приложения каждой силы тяжести равно нулю.

При установившемся движении машины ее кинетическая энергия не изменяется и сумма работ приложенных к ней движущих сил и сил сопротивления равна нулю:

.

Так как работа сил сопротивления отрицательна, то эту сумму можно представить в виде

,

или

т.е. при установившемся движении машины работа движущих сил равна абсолютной числовой величине работы сил сопротивления. Это зна­чит, что работа, затрачиваемая на приведение машины в движение, расходуется на преодоление полезных и вредных сопротивлений:

Механический коэффициент полезного действия машины η при установившемся ее движении равен отношению полезной работы машины к работе, затраченной на приведение машины в движение:

. (10.16)

Если известны полезная мощность машины N_маш и мощность дви­гателя, приводящего ее в движение N_дв то механический коэффициент полезного действия машины

. (10.17)

Пример. Состав из 50 вагонов весом 800 кН каждый движется по подъему i=tga=0,002. Сопротивление его движению составляет 3 Н на 1 кН веса. На протяжении 750 м скорость поезда изменяется от 18 до 36 км/ч. Определить силу тяги тепловоза.

Решение. Рассматриваем поступательное движение состава как движение материальной точки. Применяем к его движению теорему об изменения кине­тической энергии на перемещении М_оМ₁ (рис. 10.9). Скорость поезда на этом перемещении изменяется от = 18 км/ч = 5 м/с до = 36 км/ч = 10 м/с. На состав действуют постоянные по модулю и направлению силы —сила тяги тепловоза , вес состава , нормальная реакция рельсов и сила сопротивления движению , модуль которой равен 0,003G. Составляем урав­нение:

. (10.18)

Работу силы тяги на перемещении М_оМ₁ определяем по формуле:

.

Работа силы тяжести зависит только от вертикального перемещения Н :

.

Так как угол а мал, то sin а ≈tg а= i и

.

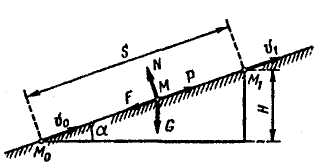
Рис. 10.9

Работа силы перпендикулярной перемещению, равна нулю.

Работа силы сопротивления определяется по формуле:

.

Подставляем в уравнение (10.18) значение массы состава т= G/g и значе­ния работы всех приложенных к нему сил:

,

откуда

.

Подставляя числовые значения, находим модуль силы тяги тепловоза:

.

Задача 3. Определение скорости и ускорения тела с помощью теоремы об изменении кинетической энергии механической системы

Механическая система под действием сил тяжести приходит в движение из состояния покоя. Учитывая трение скольжения тела 3, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость и ускорение тела 1 в тот момент, когда пройденный им путь станет равным S ( рис1, а).

В задаче принять , , , , см, , , м.

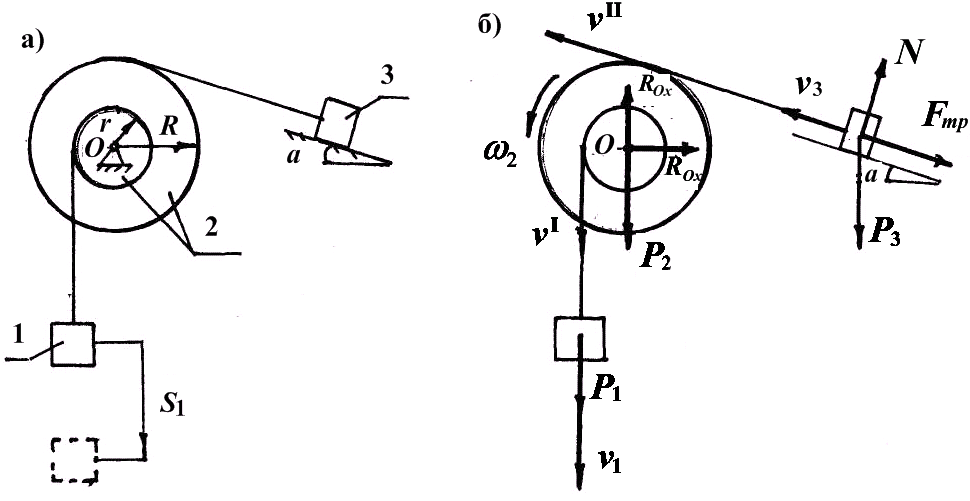
Рис. 1

Решение.

1. Составление расчетной схемы. На механическую систему действуют активные силы . Применяя принцип освобождаемости от связей только к внешним связям системы, покажем реакции шарнирно-неподвижной опоры тела 2 и шероховатой наклонной поверхности. Направления скоростей тел системы изобразим с учетом того, что тело 1 спускается (рис1, б).

2. Выбор теоремы. Задачу решим применяя теорему об изменении кинетической энергии системы.

,

где и Т - кинетическая энергия системы в начальном и конечном положениях; - алгебраическая сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное; - сумма работ внутренних сил системы на том же перемещении.

Для рассматриваемой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями

.

Так как в начальном положении система покоилась, то = 0. Следовательно,

.

3. Составление уравнения.

а) Определение кинетической энергии системы в конечном положении. Кинетическая энергия системы представляет собой сумму кинетических энергий тел 1, 2 и З.

.

Кинетическая энергия груза 1, движущегося поступательно

.

Кинетическая энергия блока 2, совершающего вращение вокруг оси Oz, перпендикулярной плоскости чертежа

.

Кинетическая энергия тела 3 в его поступательном движении

.

Таким образом,

. (1)

Выражение кинетической энергии содержит неизвестные скорости всех тел системы, а определить необходимо , поэтому избавимся от лишних неизвестных, составив уравнения связей.

б) Уравнения связей.

Уравнения связей это не что иное, как кинематические соотношения между скоростями и перемещениями точек системы. При составлении уравнений связей выразим все неизвестные скорости и перемещения тел системы через скорость и перемещение груза 1.

Скорость любой точки обода блока малого радиуса равна скорости тела 1, а также произведению угловой скорости тела 2 и радиуса вращения :

.

Отсюда выразим угловую скорость тела 2

. (2)

Вращательная скорость любой точки обода блока большого радиуса с одной стороны равна произведению угловой скорости блока и радиуса вращения, а с другой - скорости тела 3.

.

Подставив значение угловой скорости, получим

. (3)

Проинтегрировав при нулевых начальных условиях выражения (2) и (3), запишем соотношение перемещений точек системы

. (4)

. (5)

Зная основы зависимости скоростей точек системы, вернемся к выражению кинетической энергии (1) и подставим в него уравнения (2) и (3).

.

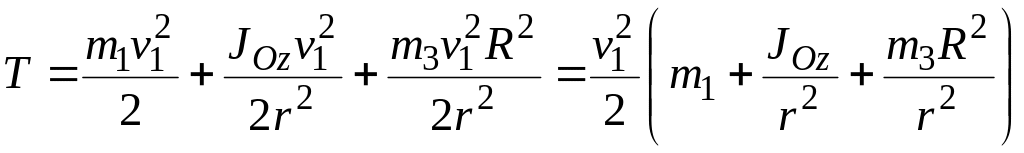Заметим, что момент инерции тела 2 равен

.

Подставляя значения масс тел и момента инерции тела 2, запишем

.

в) Определение суммы работ всех внешних сил системы на заданном перемещении.

.

Работа силы тяжести тела 1

.

Работа сил , , равна нулю, так как эти силы приложены к неподвижной точке.

.

Работа силы тяжести тела 3

.

Работа нормальной реакции тела 3 равна нулю, так как сила перпендикулярна направлению движения

.

Работа силы трения скольжения

,

так как

,

то

.

Сумма работ внешних сил

Подставляя значения масс тел, соотношение перемещений (5) и числовые параметры запишем

Теперь, согласно теореме об изменении кинетической энергии системы приравняем значения Т и

. (6)

4. Определение неизвестных.

Скорость тела 1 получим из выражения (6)

Ускорение тела 1 можно подсчитать, продифференцировав по времени равенство (6)

,

где .

Тогда

.

Пример. Груз 1 массы , опускающийся без раскачивания под действием силы тяжести, приводит в движение через посредство троса и двухступенчатого блока 2 каток 3 массы , поднимаю­щийся по наклонной плоскости, образующей с горизонтом угол (рис. 5.10). Определить ускорение груза, если I₂ - момент инерции блока относительно оси вращения; R₂, r₂ - радиусы ступеней блока; I₃ - момент инерции катка относительно оси, проходящей через центр масс; R₃ - радиус катка; - коэффициент трения качения. Ка­чение катка происходит без скольжения. Массой троса пренебречь. Сопротивление на оси блока не учитывать.

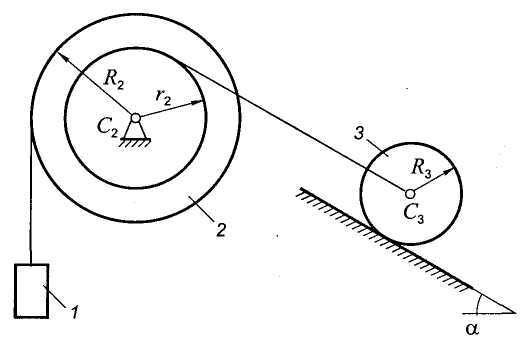
Рис. 5.10

Решение. Рассмотрим систему, состоящую из тел 1-3 и троса. Эта система имеет одну степень свободы, поскольку тела, входящие в ее состав, являются абсолютно твердыми, трос нерастяжимым, каче­ние катка происходит без скольжения, а раскачивание при движении груза отсутствует. Так как целью задачи является определение уско­рения груза, то в качестве параметра, определяющего положение сис­темы, естественно принять координату х центра масс груза (рис. 5.11).

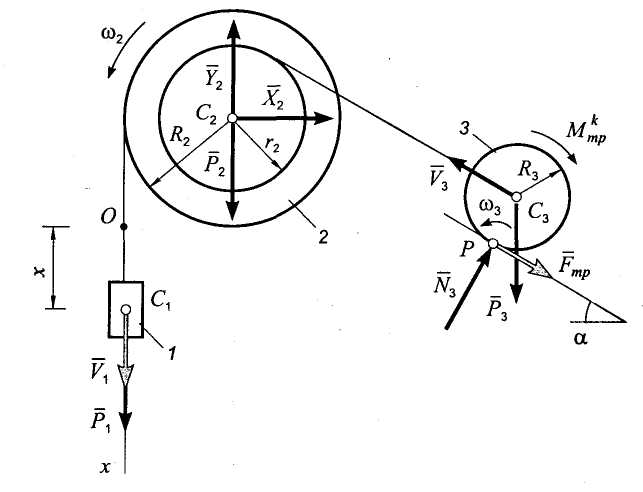
Рис. 5.11

Составим дифференциальное уравнение движения системы. Воспользуемся для этой цели теоремой об изменении кинетической энергии в дифференциальной форме для неизменяемых систем

. (5.78)

Определим кинетическую энергию системы как сумму кинети­ческих энергий тел, входящих в ее состав:

.

Кинетическая энергия груза, движущегося поступательно со скоростью v₁

.

Кинетическая энергия блока, вращающегося вокруг неподвиж­ной оси С₂ с угловой скоростью ,

.

Кинетическая энергия катка, совершающего плоское движение

.

где - угловая скорость катка; - скорость его центра масс.

Таким образом, кинетическая энергия системы

.

Поскольку

. (5.79)

то

,

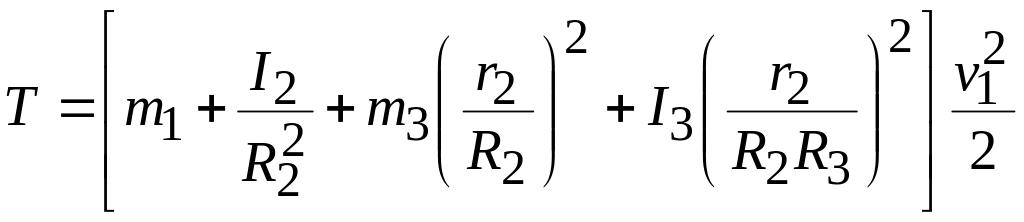или

,

где

.

Таким образом, кинетическая энергия системы представлена в форме кинетической энергии твердого тела массы , совершающего поступательное движение со скоростью, равной скорости груза.

Поскольку приведенная масса является постоянной величиной, то

. (5.80)

Определим мощность внешних сил. Внешними силами, дейст­вующими на систему, являются силы тяжести тел , реакции подшипников оси блока и реакции плоскости: нормальная реакция , сила трения и момент трения качения . Заме­тим, что мощности сил равны нулю, так как эти силы приложены в точках, скорости которых равны нулю: точка С₂ неподвижна, а точка Р является мгновенным центром скоростей катка. Мощности остальных сил отличны от нуля: мощность силы тяжести груза равна ; мощность силы тяжести катка равна ; мощность момента трения качения рав­на , где , причем нормальная реакция плоскости .

Таким образом, мощность внешних сил

.

Подставляя в последнюю формулу соотношения (5.79) и учиты­вая значение момента трения качения, получаем

,

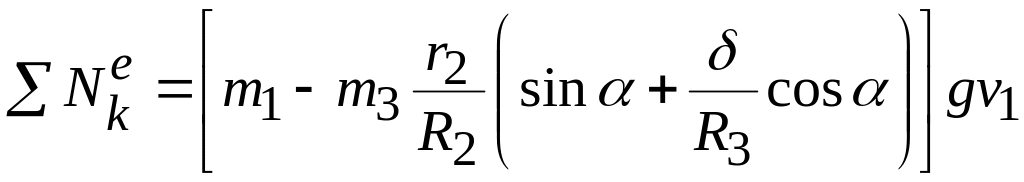или

, (5.81)

где

.

Приравнивая, согласно (5.78), правые части соотношений (5.80) и (5.81), получаем дифференциальное уравнение движения системы

. (5.82)

Поскольку приведенная сила является постоянной величи­ной, то проекция ускорения груза на ось х

.

Пример. Двухступенчатый барабан 1 имеет горизонтальную ось вращения С₁. На ступени барабана навиты нити, к концам кото­рых привязаны грузы 2 и 3 равной массы т, причем груз 3 стоит на плоскости (рис. 5.12). В некоторый момент времени грузу 2 сообща­ется скорость , направленная вертикально вниз. На какую высоту Н поднимется груз 3 над плоскостью, если R, r - радиусы ступеней барабана; I - момент инерции барабана относительно оси вращения; М_с - постоянный момент сопротивления на оси барабана. Массу ни­тей не учитывать. Грузы при движении не раскачиваются.

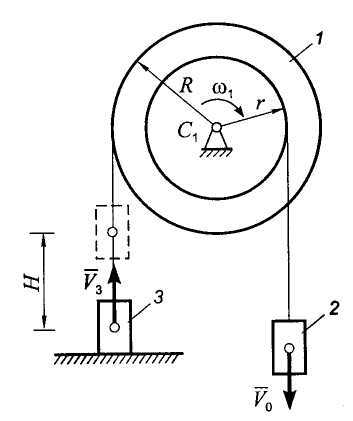
Рис. 5.12

Решение. Рассмотрим систему, состоящую из тел 1-3 и нитей. Поскольку тела, входящие в ее состав, являются абсолютно твердыми, нити нерастяжимыми, а рас­качивание грузов при движении отсутствует, то система имеет одну степень свободы. Так как движение системы происходит под действием постоянных сил, работу которых можно вычис­лить, не зная закона движения системы, то для решения задачи удобно использовать теорему об изменении кинетической энергии в конечной форме для неизме­няемых систем

. (5.83)

Определим приращение кинети­ческой энергии системы на рассматриваемом перемещении. Кинетическая энергия системы в на­чальном положении равна сумме кинетических энергий барабана, вращающегося вокруг неподвижной оси, и грузов, движущихся по­ступательно:

.

где - угловая скорость барабана в начальном положении; v₃ -скорость груза 3 в начальном положении (рис. 5.12).

Поскольку

,

то

.

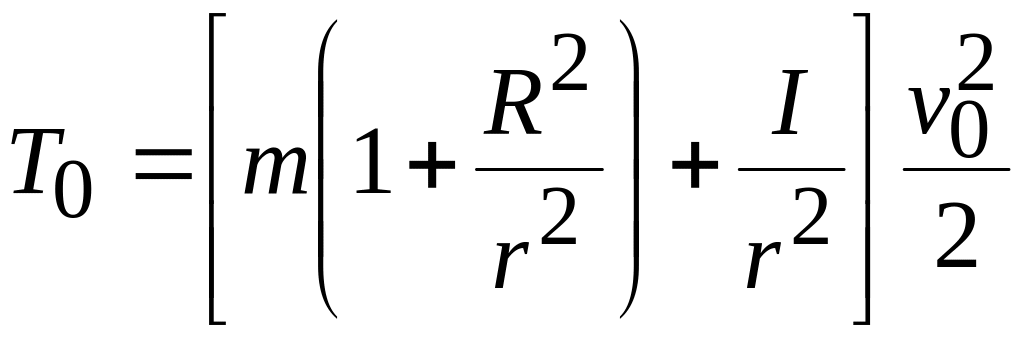Так как кинетическая энергия системы в конечном положении Т=0,то

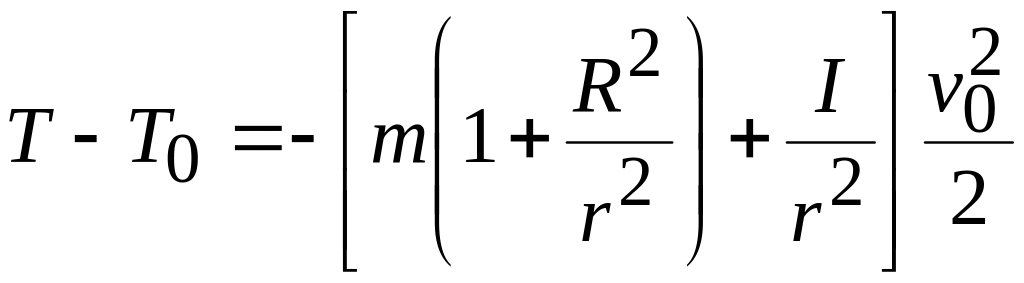. (5.84)

Вычислим теперь работу внешних сил на перемещении системы из начального положения в конечное. Внешними силами, действующими на рассматривае­мую систему, являются силы тяжести тел , реак­ции подшипников оси бара­бана и момент сопро­тивления М_с. (рис. 5.13). Ра­бота силы тяжести барабана равна нулю, так как эта сила приложена в неподвижной точке: центр масс барабана расположен на оси вращения. Работа силы тяжести груза 2 равна , где h - вы­сота, на которую опустится груз 2 при переходе из на­чального положения в ко­нечное. Работа силы тяжести груза 3 равна . Работа момента сопротивления равна , где -угол поворота барабана.

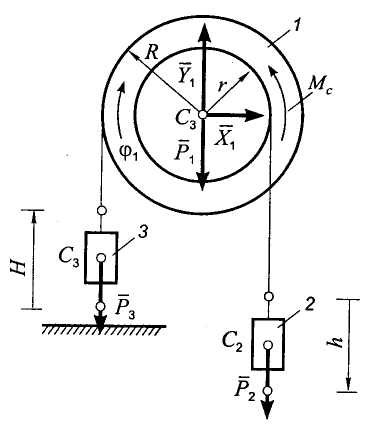
Рис. 5.13

Таким образом,

.

Но

,

поэтому

. (5.85)

Приравнивая, согласно (5.83), правые части формул (5.84) и (5.85)

находим

,

находим

.

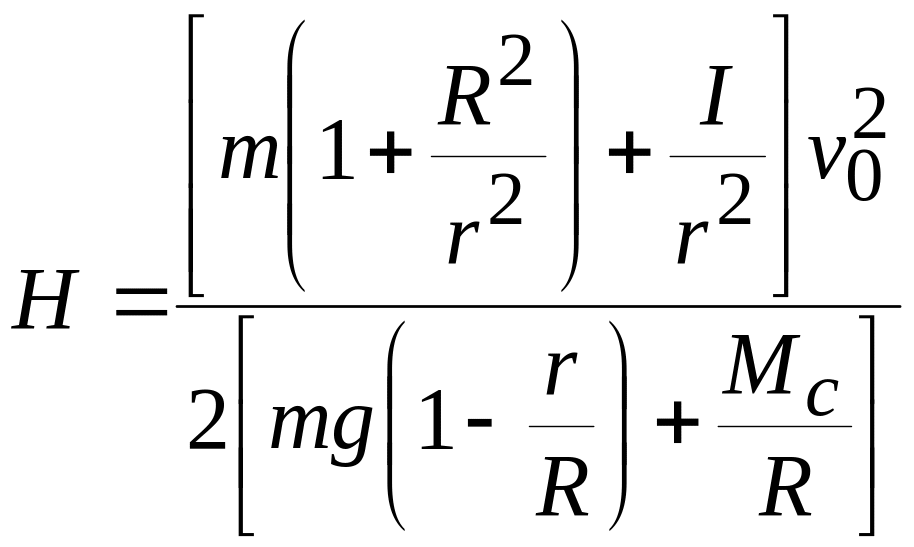Пример. Груз 3 массы т₃ перемещается по наклонной плоско­сти, образующей угол с горизонтом, электрической лебедкой, со­стоящей из зубчатого колеса 1 радиуса R₁ и находящегося с ним в зацеплении колеса 2 радиуса R₂, на одном валу с которым находится барабан радиуса r₂, на который навивается трос, прикрепленный к грузу (рис. 5.14).

К колесу 1 приложен со стороны мотора постоянный вращающий момент М₁ на валу колеса 2 действует постоянный момент сопротив­ления М₂. Определить угловую скорость колеса 1 как функцию его угла поворота, если I₁ - момент инерции ведущего вала (вал и колесо l); I₂- момент инерции ведомого вала (вал, ко­лесо 2 и барабан); f -коэффициент трения скольжения груза о наклонную плоскость. Трос считать нерастя­жимым, невесомым и не сопротивляющим­ся изменению формы. Движение начинается из состояния покоя. Центры масс вращаю­щихся тел находятся на осях вращения.

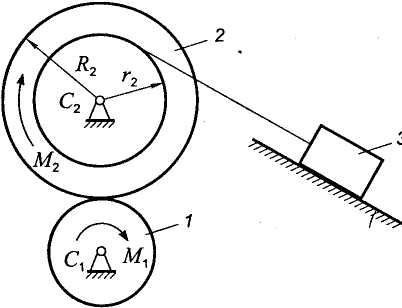
Рис. 5.14

Решение. Рассмотрим систему, состоящую из тел 1-3 и троса. Поскольку тела абсолютно твердые, а трос нерастяжимый, то систе­ма имеет одну степень свободы. Будем определять положение сис­темы с помощью угла поворота ведущего вала. Заметим также, что система является неизменяемой. Поскольку движение системы происходит под действием постоянных сил, работу которых можно вычислить, не зная закона движения системы, то для решения задачи удобно использовать теорему об изменении кинетической энер­гии в конечной форме для неизменяемых систем

. (5.86)

Определим приращение кинетической энергии системы на пе­ремещении из начального положения в некоторое конечное, зада­ваемое углом . Кинетическая энергия системы в начальном поло­жении Т₀= 0 (по условию). Кинетическая энергия системы в конеч­ном положении равна сумме кинетических энергий ведущего и ве­домого валов и груза:

,

где - угловая скорость ведущего и ведомого валов соответст­венно; v₃ - скорость груза (рис. 5.15).

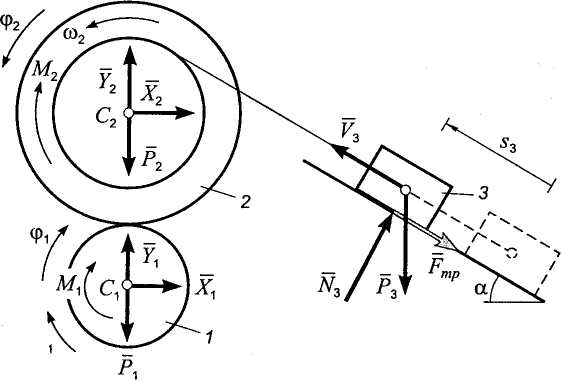
Рис. 5.15

Поскольку

,

то

,

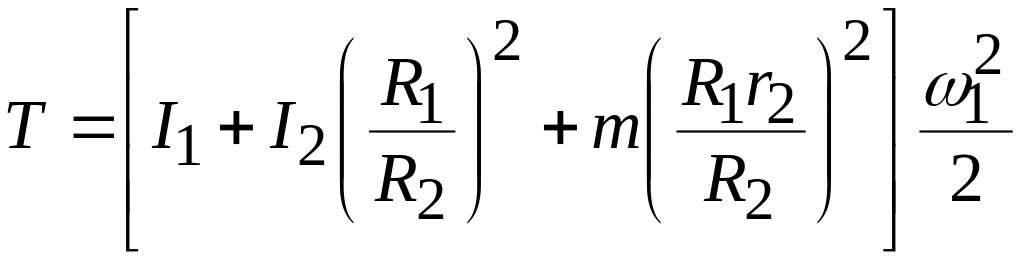или

,

где

.

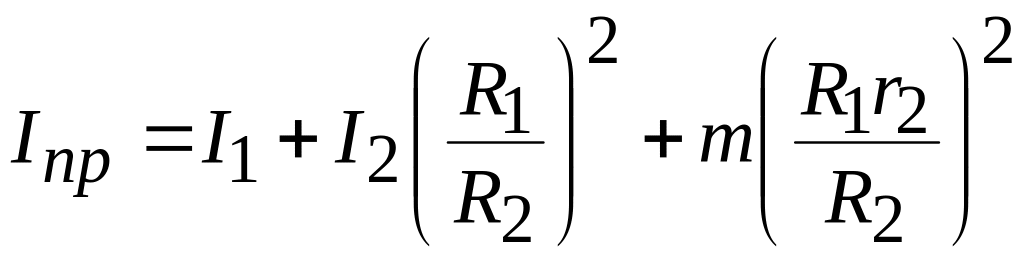Таким образом, приращение кинетической энергии системы на рассматриваемом перемещении найдено как функция угловой ско­рости ведущего вала в конечном положении:

. (5.87)

Внешними силами, действующими на систему, являются вра­щающий момент М₁ момент сопротивления М₂,__сты тяжести тел , реакции подшипников ведущего вала , реакции под­шипников ведомого вала и реакции плоскости: сила трения и нормальная реакция . Вычислим теперь работу внешних сил на перемещении системы из начального положения в конечное:

1) работа вращающего момента равна ;

2) работа момента сопротивления равна , где -угол поворота ведомого вала;

3) работы сил , а также , равны нулю, так как эти силы приложены в неподвижных точках;

4) работа силы равна нулю, так как эта сила перпендику­лярна перемещению точки ее приложения;

5) работа силы равна , где s₃ - перемещение груза;

6) работа силы трения равна ( ), где .

Таким образом,

.

Но

,

поэтому

.

или

, (5.88)

где

.

Приравнивая, согласно (5.86), правые части формул (5.87) и (5.88), получаем

,

откуда

. (5.89)

Таким образом, искомая зависимость имеет вид:

.

Лекция 11

ПРИНЦИП ГЕРМАНА-ЭЙЛЕРА-ДАЛАМБЕРА ДЛЯ

МАТЕРИАЛЬНОЙ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ

Принцип Германа-Эйлера-Даламбера для

материальной точки и механической

системы

Принцип Германа - Эйлера - Даламбера называют общий метод, с помощью которого уравнениям динамики по форме придается вид уравнений статики. Этот метод, предложенный в 1716 г. Германом и обобщенный в 1737 г. Эйлером, получивший название петербургского принципа, часто называют началом или принципом Даламбера, хотя действительная сущность начала Даламбера не аналогична петербург­скому принципу. Предположим, что материальная точка М под действием системы сил движется с ускорением (рис. 11.1). Основное уравнение динамики имеет вид

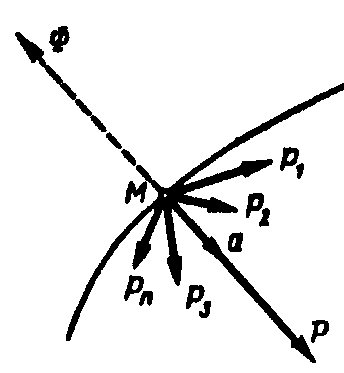
Рис. 1

Перенесем член т из левой части уравнения в правую:

.

Так как , то

. (11.1)

Полученное соотношение формулируется так: геометрическая сумма всех приложенных к точке сил и силы инерции этой точки равны пулю.

Это означает, что для решения задачи ди­намики материальной точки по принципу Германа — Эйлера — Даламбера следует помимо приложенных к точке М сил условно прило­жить к этой точке силу инерции . Тогда мно­гоугольник рассматриваемой системы сил , будет замкнут и суммы их проек­ций на координатные оси будут равны нулю.

Как известно, в действительности сила инерция материальной точки приложена не к ней, а к телу, сообщающему точке ускорение. Приложение силы инерции к точке является лишь условным, приемом, сводящим задачу динамики по форме решения к задаче статики. Благодаря простоте этот метод получил широкое применение во мно­гих прикладных дисциплинах. В ряде случаев он обеспечивает наиболее простое и удобное решение задач динамики.