Воспользуемся основным уравнением динамики

.

Спроецируем векторы, входящие в это уравнение, на касательную, вдоль которой направлен орт :

.

Подставляем в это уравнение зна­чение и умножаем обе части равен­ства на :

. (10.1)

Левая часть полученного равенства представляет собой дифференциал кинетической энергии точки, а пра­вая часть является суммой элементарных работ, приложенных к точке сил. Таким образом,

. (10.2)

Равенство (10.2) показывает, что дифференциал кинетической энер­гии материальной точки равен сумме элементарных работ сил, прило­женных к точке. Проинтегрируем обе части равенства (10.1) в пределах, соответ­ствующих начальному и конечному положениям точки М₁ и М₂:

,

откуда

(10.3)

Уравнение (10.3) выражает теорему об изменении кинетической энергии материальной точки: изменение кинетической энергии мате­риальной точки на некотором ее перемещении равно алгебраической сумме работ всех действующих на эту точку сил на том же перемещении.

Если сумма работ сил положительна, то v₂>v₁, т.е. кинетическая энергия точки возрастает, если же эта сумма отрицательна, то v₂<v₁, т. е. кинетическая энергия точки убывает. Применяя эту теорему к дви­жению несвободной материальной точки, следует освободить эту точку от связей, заменив их действие соответствующими реакциями. При движении точки по неподвижной гладкой поверхности реакция этой поверхности направлена по нормали к этой поверхности, а потому ее работа при перемещении точки по поверхности равна нулю. Следовательно, изменение кинетической энергии материальной точ­ки в этом случае равно сумме работ на соответствующем перемеще­нии всех задаваемых сил, приложенных к точке. При движении мате­риальной точки по неподвижной шероховатой поверхности действует сила трения , направленная противоположно скорости точки. Работу этой силы можно определить по формуле:

.

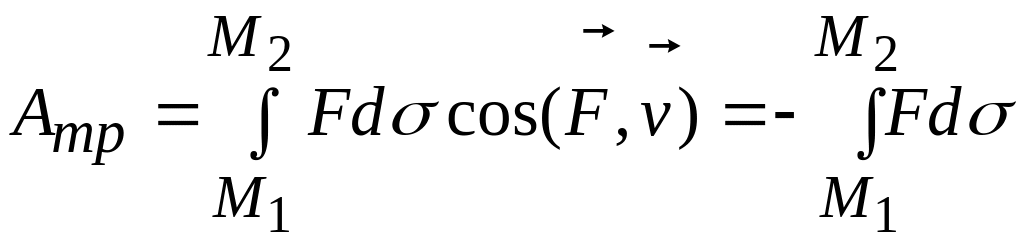Здесь , так как направления силы трения и скорости точки противоположны. В правой части уравнения (10.3) в этом случае кроме работ задаваемых сил содержится и работа силы тре­ния .

Теорема об изменении кинетической энергии материальной точки в относительном движении. Ранее установлено, что относительное движение материальной точки можно рассматривать как абсолютное, если к силам, приложен­ным к точке, присоединить переносную и кориолисову силы инерции. Из этого следует, что, применяя к относительному движению мате­риальной точки теорему об изменении кинетической энергии, необхо­димо к работе действующих сил добавить работу переносной и кориолисовой сил инерции Ф_е и Ф_с.

Однако кориолисово ускорение , а следовательно, и кориолисова сила инерции Ф_с, всегда перпендикулярны относительной скорости точки . Следовательно, работа кориолисовой силы инерции на относительном перемещении точки равна нулю и не входит в уравнение изменения кинетической энергии. Поэтому это уравнение для относительного движения точки имеет вид

. (10.4)