2. Теоремы о работе силы.

Т е о р е м а I. Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ cоcmавляющих сил на том же перемещении.

Предположим, что на точку М действуют силы (рис. 9.6). Равнодействующая этих сил

.

Если точка М получает элементарное перемещение , то элементар­ная работа равнодействующей силы на этом перемещении

Для вычисления работы равнодействующей силы на конечном участке пути M₁M₂ воспользуемся формулой (9.12):

.

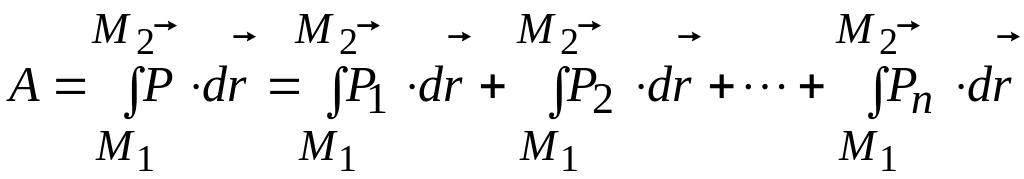полученная сумма криволинейных интегралов представляет собой сумму работ отдельных сил на конечном участке пути M₁M₂. Таким образом,

.

Т е о р е м а 2. Работа постоянной по модулю и направлению силы на результирующем перемещении равна алгебраической сумме работ этой силы на составляющих перемещениях.

Предположим, что точка приложения постоянной по модулю и направлению силы получает совокупность последо­вательных перемещений (рис. 7 выполнен для n= 3). Результирующее перемещение точки М

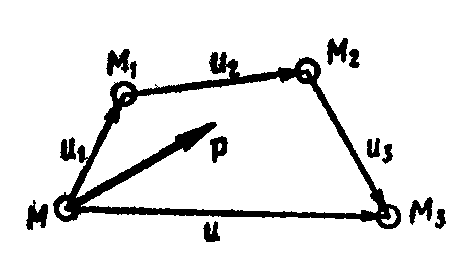
Рис. 9.7

.

Работа силы на этом перемещении определяется по формуле (9.2):

.

Полученная сумма представляет собой сумму работ силы на составляющих перемещениях. Таким образом,

.

На основании этой теоремы при вычислении работы постоянной силы на криволинейном перемещении криволинейное перемещение можно заменить прямолинейным. При и= 0, т. е. в случае замкнутого контура, работа постоянной силы равна нулю.

Изображение работы в виде площади. Установлено, что работа переменной силы на конечном перемещении М₁М₂ определяется криво­линейным интегралом, взятым вдоль дуги М₁М₂ траектории, которую описывает точка приложения силы.

Криволинейный интеграл, определяющий работу силы, вычисляется обычно аналитически с помощью формулы (9.13) или графически на основе формулы (9.11).

Для графического определения работы силы на перемещении М₁М₂ (см. рис. 9.3) используется график (рис. 9.8). По оси абсцисс этого графика отложены значения дуговой координаты точки s, а по оси ординат - соответствующие значения проекции силы на касатель­ную . Построенная кривая изображает зависимость от s. Элементарная работа силы согласно (9.6)

.

На рис. 9.8 эта величина изображается площадью элементарного прямоугольника, имеющего основание ds и высоту . Работа силы на перемещении М₁М₂ изобразится площадью фигуры acdb, ограни­ченной осью абсцисс, кривой =f(s) и ординатами aс и bd, соот­ветствующими точкам M₁ и М₂:

А = пл. acdb.

Если проекция силы на касательную отрицательна, то соответ­ствующая площадь расположится ниже оси абсцисс и работа силы будет отрицательна. Для примера рассмотрим проводимое в механи­ческих лабораториях графическое вычисление работы, затрачиваемой на разрыв образца. На рис. 9.9 изображена полученная опытным путем диаграмма растяжения образца. По оси ординат отложена величина растягивающей

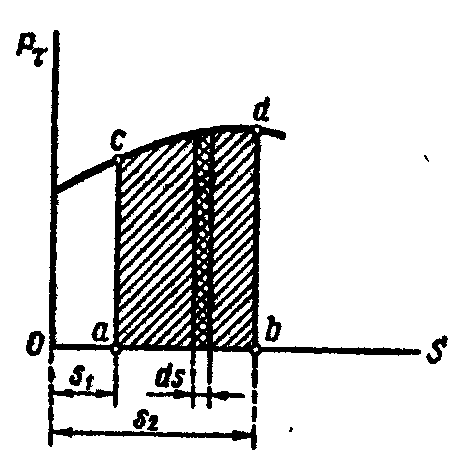
Рис. 9.8 Рис. 9.9

силы, а по оси абсцисс - производимое ею абсолютное удлинение образца, т. е. перемещение точки приложения силы. Точка В обозначает предел пропорциональности, С - предел текучести, D — наибольшую нагрузку, воспринимаемую образцом, К - нагрузку и момент разрыва образца. Работа, затрачиваемая на растяжение образца до предела пропор­циональности, определяется площадью треугольника OBO₁. Площадь obcdko₃ определяет всю работу, затрачиваемую на разрыв испытуемого образца. Величину этой площади находят обычно с помощью планиметра или путем вычислений.

За единицу работы в системе МКС принимается 1 джоуль (Дж), т.е. работа силы, равной 1 Н на перемещении в 1 м по направлению силы; в системе СГС - 1 эрг, т. е. работа силы, равной 1 д на пере­мещении в 1 см по направлению силы; в системе МКГСС за единицу работы принимается 1 кгсм, т. е. работа силы, равной 1 кгс на пере­мещении в 1 м по направлению силы.

1 джоуль = 10⁷ эрг =0,102 кг∙см, 1 кг∙см= 9,81 Дж.

Изменение работы силы, отнесенное к единице времени, называется мощностью силы. Если в течение малого промежутка времени dt сила совершает работу , то мощность этой силы

. (9.14)

Таким образом, мощность силы равна скалярному произведению векторов силы и скорости ее точки приложения.

Аналитическое выражение мощности силы имеет вид

, (9.15)

где — проекции скорости точки приложения силы на оси координат. Из формулы (9.14) имеем

. (9.16)

Если направления силы и скорости совпадают, то

. (9.17)

За единицу мощности в системе МКС принимается 1 ватт (Вт)=1 Дж/с = 0.102 кг∙см/с, а в системе СГС - 1 эрг/с.

В системе МКГСС за единицу мощности принимается 1 кг∙см/с.

Кроме того, применяются следующие единицы мощности: 1 кило­ватт (кВт)=10³ Вт=102 кг∙см/с = 1,36 лошадиной силы (л. с.); 1 ло­шадиная сила= 75 кг∙см/с = 736 Вт. В технике часто за единицу работы принимается 1 киловатт-час (кВтч), т.е. работа, совершаемая в течение одного часа движущей сило машины, мощность которой равна 1 киловатту; 1 киловатт-час=1000∙3600 ватт-секунд = 36∙10⁵ джоуль.