
- •Курс лекций по Динамике
- •Лекция 1 введение в динамику. Динамика точки
- •1 Законы динамики Галлилея-Ньютона
- •Система единиц механических величин. Для измерения механических величин применяются две системы единиц: физическая и техническая.
- •2. Дифференциальные уравнения движения материальной точки
- •Проекции ускорения на касательную и главную нормаль определяются по формулам из кинетики:
- •3 Первая основная задача динамики
- •2 Решение задачи при действии постоянной силы
- •Решение задачи при действии силы, зависящей от времени
- •4 Решение задачи при действии силы, зависящей от скорости точки
- •5 Решение задачи при действии силы, зависящей от положения точки
- •Задача 1. Определение скорости точки с помощью дифференциальных уравнений
- •Затухающие свободные колебания, случаи апериодического движения
- •Частота затухающих колебаний
- •Введем в полученное уравнение гиперболические функции
- •Общее решение уравнения (4.3) получает вид
- •В этом случае амплитуда вынужденных колебаний
- •2. Явление биений и резонанса
- •Обозначим
- •Свободные колебания определяются уравнением
- •Вынужденные колебания при резонансе
- •Вынужденные колебания точки с учетом сопротивления движению.
- •При этих обозначениях дифференциальное уравнение движения точки имеет вид
- •Корни этого уравнения
- •В этом случае
- •2 Характеристики инертности механической системы
- •3 Теорема о моментах инерции твердого тела относительно параллельных осей
- •4. Примеры определения моментов инерции масс тел простейшей формы
- •Моменты инерции некоторых тел
- •Кроме того, введем обозначения
- •Импульс силы
- •В проекциях на координатные оси это равенство принимает вид
- •3. Теорема об изменении количества движения
- •Пользуясь этими выражениями, получаем
- •Из уравнения (7.7) следует, что если
- •Теорема об изменении кинетического момента механической системы относительно центра и оси
- •Кинетический момент механической системы относительно центра о
- •2. Дифференциальные уравнения плоского движения твердого тела
- •Формулу (г) можно представить в виде: .
- •3. Дифференциальные уравнения сферического движения твердого тела
- •4. Элементарная теория гироскопа
- •2. Теоремы о работе силы.
- •3. Работа силы тяжести, силы упругости и силы тяготения
- •Проекции силы на оси координат будут
- •Элементарная работа силы упругости.
- •4. Работа сил, приложенных к твердому телу.
- •Работа на конечном перемещении
- •Воспользуемся основным уравнением динамики
- •2. Теорема о кинетической энергии механической системы в общем случае движения
- •3. Кинетическая энергия твердого тела
- •4. Теорема об изменении кинетической энергии механической системы
- •Сумма работ внутренних сил твердого тела на любом перемещении равна нулю, т. Е. . Для твердого тела уравнение (14) принимает вид
- •Механический коэффициент полезного действия машины
- •2. Принцип Германа - Эйлера - Даламбера для несвободной механической системы
- •3. Приведение сил инерции точек твердого тела к простейшему виду
- •4. Определение динамических реакций подшипников при вращения твердого тела вокруг неподвижной оси
- •Возможные (виртуальные) перемещения механической системы. Идеальные связи
- •2. Принцип возможных перемещений
- •3. Применение принципа возможных перемещений к простейшим машинам
- •2 Обобщенные силы и примеры их вычисления
- •На основании (13.8) имеем
- •Выражение обобщенных сил через проекции сил на неподвижные оси декартовых координат. Случай сил, имеющих потенциал
- •3. Общее уравнение динамики в обобщенных силах. Приведем общее уравнение динамики (13.4) к виду
- •Задача 4. Применение общего уравнения динамики к изучению механической системы
- •Понятие об устойчивости равновесия механической системы
- •Поэтому состояние покоя метронома устойчиво, если
- •1. Уравнения Лагранжа второго рода
- •Задача 5. Исследование механической системы с применением уравнений Лагранжа второго рода
- •2. Кинетический потенциал. Циклические координаты
- •Циклические координаты. Циклические интегралы. Обобщенные координаты, которые не входят явно в выражение кинетического потенциала l, называются циклическими координатами.
- •Кинетический потенциал точки
- •3. Вариационный принцип Гамильтона-Остроградского Общие понятия
- •Общее уравнение динамики имеет вид
- •2 Коэффициент восстановления при ударе. Удар тела о неподвижную преграду
- •3 Прямой центральный удар двух тел
- •4 Потеря кинетической энергии при ударе двух тел. Теорема карно
- •Начальная кинетическая энергия тел
- •Кинетическая энергия тел в конце удара
- •Потеря кинетической энергии тел за время удара
- •Формула принимает вид
- •5 Действие ударных сил на твердое тело, вращающееся вокруг неподвижной оси, и на твердое тело, совершающее плоское движение
4. Элементарная теория гироскопа
Гироскопом обычно называется твердое тело, вращающееся вокруг оси материальной симметрии, одна из точек которой неподвижна.
Предположим,
что гироскоп имеет неподвижную точку
О и
ось симметрии
О
(рис. 8.7, а).
Если гироскоп вращается вокруг оси О
с угловой
скоростью
![]() и положение оси О
не изменяется, то вектор угловой скорости
гироскопа
направлен по оси О
. Его проекции на подвижные оси координат:
и положение оси О
не изменяется, то вектор угловой скорости
гироскопа
направлен по оси О
. Его проекции на подвижные оси координат:
![]()
Как установлено ранее, ось симметрии О является главной осью
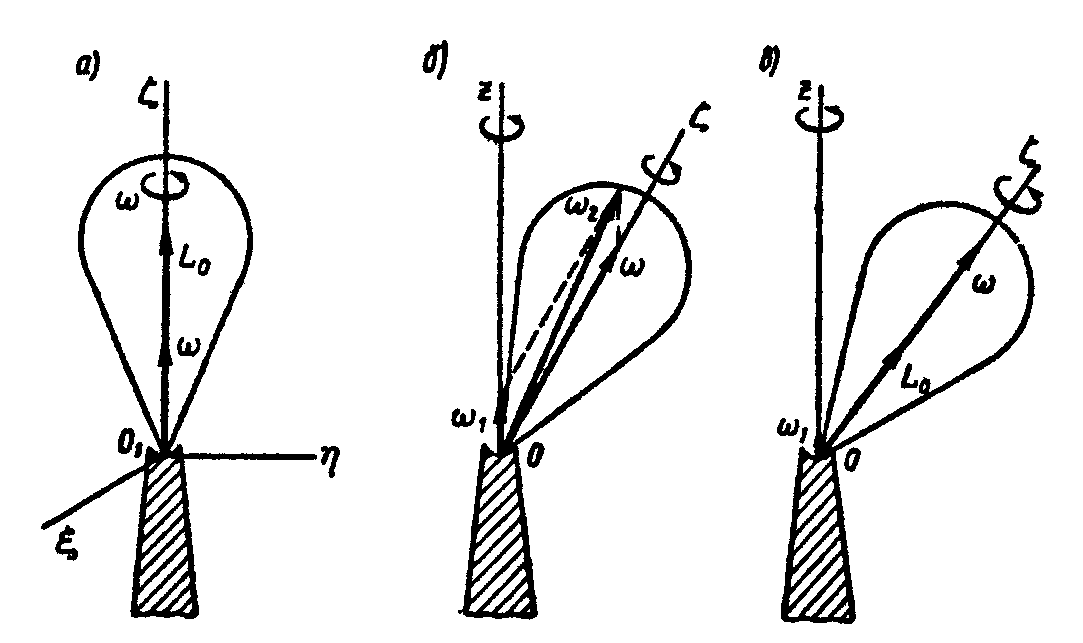
Рис. 8.7
инерции
для всех своих точек, в том числе и для
точки О.
Поэтому кинетические моменты гироскопа
относительно осей
![]() равны:
равны:
![]() ,
где
,
где
![]() -
момент инерции гироскопа относительно
оси О
.
-
момент инерции гироскопа относительно
оси О
.
Кинетический
момент гироскопа
![]() относительно
неподвижной точки О
относительно
неподвижной точки О
![]() .
.
Рассмотрим
теперь сложное движение гироскопа,
состоящее
из
вращения
вокруг его оси симметрии О
с угловой скоростью
и вращения вместе с этой осью вокруг
неподвижной оси Oz
с угловой
скоростью
![]() (рис. 8.7, б).
(рис. 8.7, б).
В
этом случае вектор абсолютной угловой
скорости гироскопа
![]() определяется диагональю параллелограмма,
построенного на угловых скоростях
составляющих вращений:
определяется диагональю параллелограмма,
построенного на угловых скоростях
составляющих вращений:
![]() .
.
Кинетический момент гироскопа относительно точки О можно определить по его проекциям на подвижные оси координат .
В
этом случае направление
не совпадает с направлением оси гироскопа
![]() .
Если угловая скорость вращения гироскопа
вокруг его оси симметрии
.
Если угловая скорость вращения гироскопа
вокруг его оси симметрии
![]() во много раз больше угловой скорости
вращения самой этой оси
во много раз больше угловой скорости
вращения самой этой оси
![]() ,
то направления векторов
,
,
а следовательно,
,
то направления векторов
,
,
а следовательно,
![]() и
весьма близки между собой.
и
весьма близки между собой.
В
дальнейшем, полагая, что угловая скорость
вращения гироскопа вокруг его оси
симметрии во много раз превышает угловую
скорость
![]() вращения самой оси (рис. 8.7, в),
условимся считать кинетический момент
гироскопа относительно неподвижной
точки О
направленным
вдоль оси симметрии гироскопа и равным
вращения самой оси (рис. 8.7, в),
условимся считать кинетический момент
гироскопа относительно неподвижной
точки О
направленным
вдоль оси симметрии гироскопа и равным
![]() .
(8.12)
.
(8.12)
На этом условии основана приближенная теория гироскопических явлений.
Гироскопом
с тремя степенями свободы называется
гироскоп, движение которого ограничено
только наличием одной неподвижной
точки. Положение твердого тела, одна из
точек которого неподвижна, можно
определить путем задания трех эйлеровых
углов:
![]() и
и
![]() .
Из этого следует, что такое тело имеет
три
степени
свободы. Гироскоп с тремя степенями
свободы, быстро вращающийся вокруг
своей оси, обладает особым физическим
свойством - оказывать сопротивление
силам, стремящимся сместить его ось.
.
Из этого следует, что такое тело имеет
три
степени
свободы. Гироскоп с тремя степенями
свободы, быстро вращающийся вокруг
своей оси, обладает особым физическим
свойством - оказывать сопротивление
силам, стремящимся сместить его ось.
Гироскоп с двумя степенями свободы не обладает способностью противодействовать изменению направления его оси вращения.
Гироскопы получили широкое применение в различных областях техники: на транспорте, в морском флоте, в авиации, в военном деле и т. д. Так, например, гироскопический эффект используется при езде на велосипеде. Гироскопические устройства обеспечивают также устойчивость движения двухколесного автомобиля и вагона однорельсовой железной дороги.
С помощью гироскопических устройств по заданному курсу направляются движения судов в открытом море и совершаются слепые полеты самолетов. Гироскопические приборы используются для управления полетом баллистической ракеты и обеспечивают движение в заданном направлении торпеды.
Для того чтобы обеспечить пуле и снаряду устойчивость в полете, ствол винтовки и орудия снабжают винтовой нарезкой. Тогда при выходе из ствола пуля и снаряд получают быстрое вращение вокруг продольной оси и приобретают свойства быстровращающегося гироскопа, обеспечивающие их устойчивость в полете
Лекция 9
РАБОТА. ТЕОРЕМЫ О РАБОТЕ СИЛ
1. Работа постоянной силы. Элементарная
работа силы
Две меры механического движения. В динамике рассматриваются два случая преобразования механического движения материальной точки или системы точек:
1) механическое движение переносится с одной механической системы на другую в качестве механического движения;
2) механическое движение превращается в другую форму движения материи (в форму потенциальной энергии, теплоты, электричества и т. д.).
Каждый
из этих случаев преобразования
механического движения имеет свои
измерители как механического движения,
так и действия силы. Когда рассматривается
преобразование механического движения
без перехода его в другую форму движения,
мерой механического движения является
вектор количества движения материальной
точки
![]() или механической системы
или механической системы
![]() .
Мерой действия силы в этом случае
является вектор импульса силы
.
Когда механическое движение превращается
в другую форму движения материи, в
качестве меры механического движения
выступает кинетическая энергия
материальной точки или механической
системы. Из элементарного курса физики
известно, что кинетическая энергия
материальной точки массой т,
движущейся со скоростью v,
равна половине произведения массы этой
точки на квадрат скорости ее движения:
.
Мерой действия силы в этом случае
является вектор импульса силы
.
Когда механическое движение превращается
в другую форму движения материи, в
качестве меры механического движения
выступает кинетическая энергия
материальной точки или механической
системы. Из элементарного курса физики
известно, что кинетическая энергия
материальной точки массой т,
движущейся со скоростью v,
равна половине произведения массы этой
точки на квадрат скорости ее движения:
![]() .
.
Итак,
существуют две различные меры механического
движения:
и
![]() - и две различные меры действия силы:
импульс силы
и работа силы
А.
Следует отметить, что измерителями
механического движения и действия
силы в первом случае являются векторные
величины
и
,
а во втором случае — скалярные величины
- и две различные меры действия силы:
импульс силы
и работа силы
А.
Следует отметить, что измерителями
механического движения и действия
силы в первом случае являются векторные
величины
и
,
а во втором случае — скалярные величины
![]() и А.
Так как изменение величины
связано с работой приложенных к телу
сил, то работа
является количественной мерой превращения
механического движения в какую-либо
другую форму движения.
и А.
Так как изменение величины
связано с работой приложенных к телу
сил, то работа
является количественной мерой превращения
механического движения в какую-либо
другую форму движения.
Работа
постоянной силы.
Рассмотрим сначала вычисление работы
постоянной по модулю и направлению
силы на прямолинейном перемещении ее
точки приложения. Предположим, что точка
приложения постоянной силы
перемещается по прямой из М
в М1
(рис. 9.1), а вектор силы
составляет с вектором перемещения
![]() угол а.
Работа силы в этом случае равна
произведению модуля силы на длину пути,
пройденною точкой приложения силы, и
на косинус угла между направлениями
вектора силы и вектора перемещения
точки ее приложения:
угол а.
Работа силы в этом случае равна
произведению модуля силы на длину пути,
пройденною точкой приложения силы, и
на косинус угла между направлениями
вектора силы и вектора перемещения
точки ее приложения:
![]() .
(9.1)
.
(9.1)
Если угол α острый, то работа силы положительна, а если тупой, то отрицательна, т.е. работа положительна, когда сила ускоряет движение, и отрицательна, когда она замедляет движение.
Из векторной алгебры известно, что скалярное произведение двух векторов
![]() .
.
Следовательно,
работа силы
на перемещении
![]()
![]() .
(9.2)
.
(9.2)
т. е. Работа постоянной по модулю и направлению силы на прямолинейном перемещении определяется скалярным произведением вектора силы на вектор перемещения точки ее приложения.
При
α
= 0
![]() ;
= 90о
;
= 90о
![]() ;
α
=180о
;
α
=180о
![]() .
.
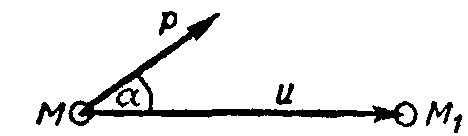
Рис. 9.1
Элементарная работа силы. Предположим, что точка приложения переменной по модулю и направлению силы перемещается по криволинейной траектории из М1 в M2 (рис. 8.2). Чтобы вычислить работу силы на этом перемещении, нужно разбить это перемещение на элементарные участки, вычислить работу силы на каждом элементарном участке как работу постоянной силы и определить предел суммы элементарных работ при стремлении числа участков к бесконечности и длины каждого из них к нулю. Элементарная работа силы на участке ММ' определяется по формуле (9.1):
![]() .
(9.3)
.
(9.3)
Здесь
Р
— модуль силы, соответствующей точке
М; dσ
— длина пути
ММ',
т. е. пройденный точкой элементарный
путь;
![]() — угол,
составленный направлением силы
и скоростью
в точке М.
Элементарную работу обозначают δА,
а не dA,
так как в общем случае она не является
дифференциалом функции. Знак работы в
выражении (1) определяется только знаком
косинуса угла
.
Будем
определять положение точки М
на траектории дуговой координатой s
= ОМ (рис. 3
и 4), а орт
— угол,
составленный направлением силы
и скоростью
в точке М.
Элементарную работу обозначают δА,
а не dA,
так как в общем случае она не является
дифференциалом функции. Знак работы в
выражении (1) определяется только знаком
косинуса угла
.
Будем
определять положение точки М
на траектории дуговой координатой s
= ОМ (рис. 3
и 4), а орт
![]() ,
направленный по касательной к траектории,
направим в сторону возрастания дуговой
координаты.
,
направленный по касательной к траектории,
направим в сторону возрастания дуговой
координаты.
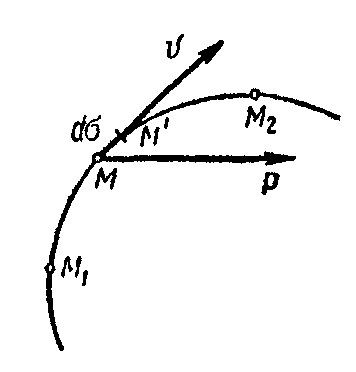
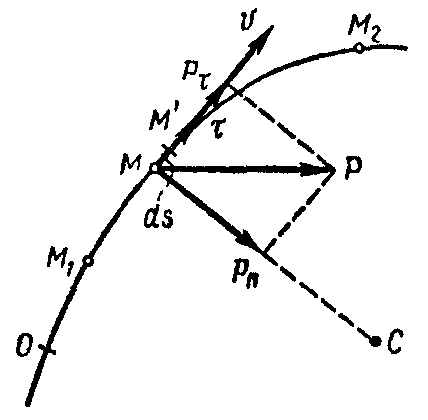
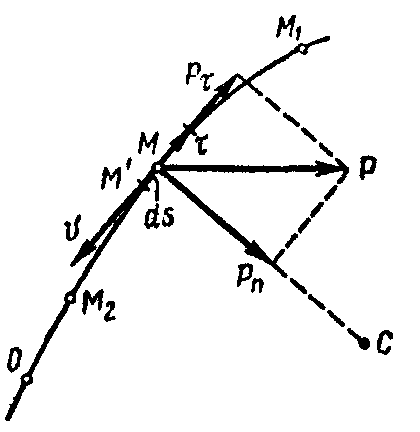
Рис. 9.2 Рис. 9.3 Рис. 9.4
Тогда при движении точки М в сторону возрастания (см. рис. 9.3) имеем:
1) ds > 0, dσ= | ds | = ds;
2)
![]() ,
так как направления
и
,
так как направления
и
![]() совпадают. Элементарная работа силы
совпадают. Элементарная работа силы
![]() .
.
При движении точки М в сторону уменьшения s (рис. 9.5) имеем:
1) ds<0; dσ = │ds│ = -ds;
2)
![]() ,
так как направления
и
противоположны. Тогда элементарная
работа силы
,
так как направления
и
противоположны. Тогда элементарная
работа силы
![]() .
.
Таким образом, при движении точки в любом направлении по траектории элементарная работа силы
![]() .
(9.4)
.
(9.4)
где
Р -
модуль силы, соответствующей точке М;
ds
- приращение дуговой координаты точки
(алгебраическая величина);
![]() - угол
между
направлением силы
и орта
,
направленного всегда по касательной в
сторону увеличения дуговой координаты.
В выражении (9.4) знак работы определяется
как знаком ds,
так и знаком
синуса угла
.
Обычно работа
силы вычисляется отдельно для участков
с движением в одном направлении.
Тогда это направление принимается за
положительное и в формуле (9.2) ds
обозначает элементарный путь dσ,
a
угол
- угол
между
направлением силы
и орта
,
направленного всегда по касательной в
сторону увеличения дуговой координаты.
В выражении (9.4) знак работы определяется
как знаком ds,
так и знаком
синуса угла
.
Обычно работа
силы вычисляется отдельно для участков
с движением в одном направлении.
Тогда это направление принимается за
положительное и в формуле (9.2) ds
обозначает элементарный путь dσ,
a
угол
![]() является углом
является углом
![]() (см. рис. 9.3). Разложим силу
на составляющие, направленные по
касательной и главной нормали к траектории
в точке М.
Проекций силы
на касательную и главную нормаль
определяются так:
(см. рис. 9.3). Разложим силу
на составляющие, направленные по
касательной и главной нормали к траектории
в точке М.
Проекций силы
на касательную и главную нормаль
определяются так:
![]() .
(9.5)
.
(9.5)
Пользуясь первой формулой (9.5), выражению (9.4) можно придать вид
![]() .
(6)
.
(6)
Формула
(9.6) показывает, что работу на перемещение
ds
совершает
только касательная составляющая силы
![]() ,
работа же
нормальной составляющей
,
работа же
нормальной составляющей
![]() ,
перпендикулярной направлению скорости
точки
,
равна нулю. Согласно (9.2), представим
элементарную работу
силы
(рис. 9.5) как скалярное произведение:
,
перпендикулярной направлению скорости
точки
,
равна нулю. Согласно (9.2), представим
элементарную работу
силы
(рис. 9.5) как скалярное произведение:
![]() ,
(9.7)
,
(9.7)
где
![]() - вектор элементарного перемещения
точки М.
- вектор элементарного перемещения
точки М.
Обозначив
проекции силы
на координатные
оси X, У,
Z,
a
проекции вектора элементарного
перемещения
![]() на оси dx,
dy,
dz,
получим скалярное произведение векторов
и
в виде
на оси dx,
dy,
dz,
получим скалярное произведение векторов
и
в виде
![]() .
(9.8)
.
(9.8)
Формула (9.8) дает выражение элементарной работы через проекции силы на оси координат. Работа силы на конечном перемещении равна сумме ее работ на элементарных участках:
![]() .
.
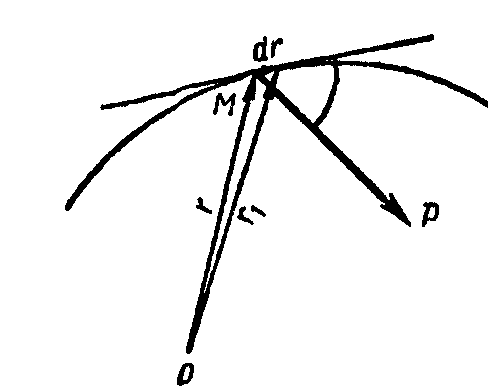
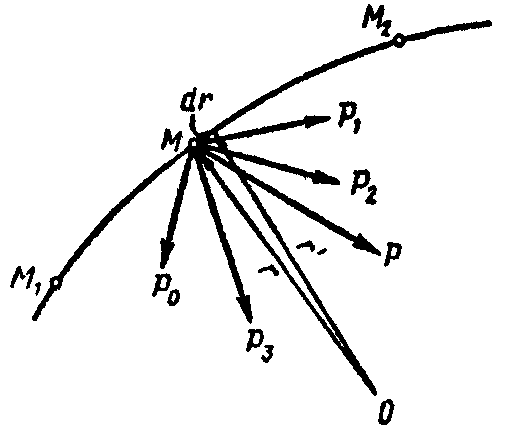
Рис. 9.5 Рис. 9.6
Пользуясь выражениями элементарной работы (9.3), (9.4), (9.6), (9.7) или (9.8) и переходя к пределу при стремлении числа участков к бесконечности, получаем следующие выражения работы силы на конечном перемещении М1М2:
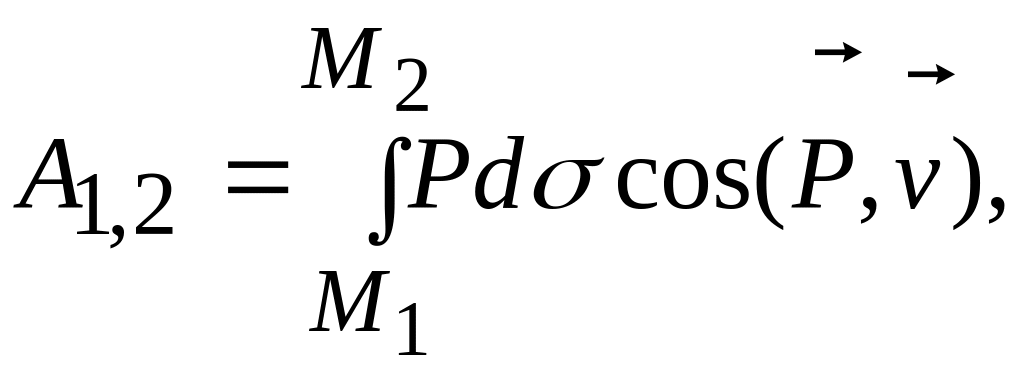 (9.9)
(9.9)
 (9.10)
(9.10)
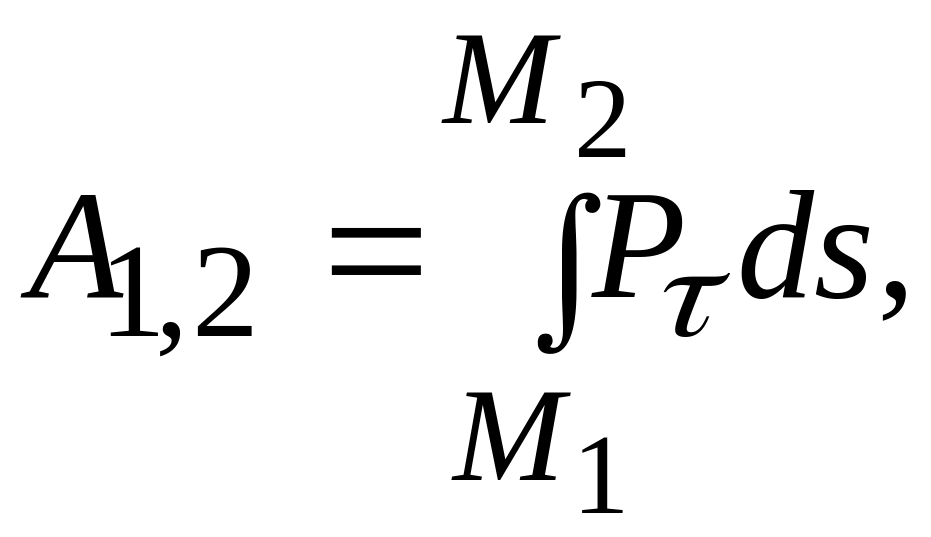 (9.11)
(9.11)
 (9.12)
(9.12)
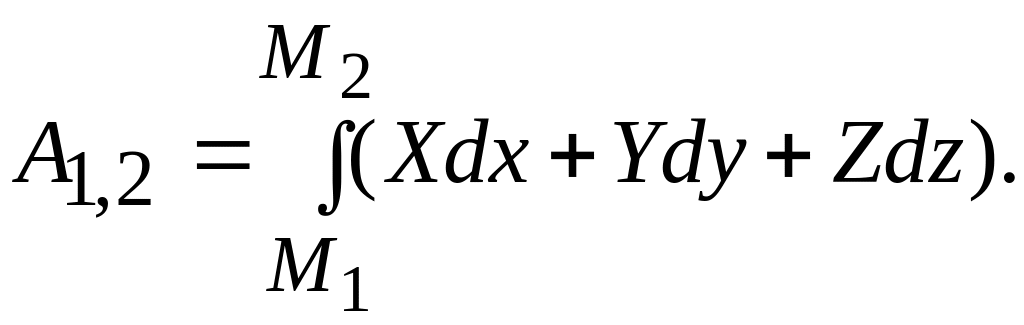 (9.13)
(9.13)
