2. Дифференциальные уравнения плоского движения твердого тела

Предположим, что твердое тело совершает плоское движение. Совместим с плоскостью чертежа плоскость, в которой движется центр масс тела, показав плоскую фигуру, полученную от сечения тела этой плоскостью (рис. 8.3). В динамике за полюс принимают не произволь­ную точку фигуры, а центр масс тела. Тогда уравнения движения плоской фигуры имеют вид

.

Если известны внешние силы , действующие на тело, то два дифференциальных уравнения движения плоской фигуры можно получить из дифференциальных уравнений:

,

где т — масса тела; X^Е и У^Е — проекции главного вектора внешних сил, приложенных к телу, на оси х и у.

Третье дифференциальное уравнение движения плоской фигуры по­лучают из уравнения :

.

Здесь L_ζr - кинетический момент тела относительно оси ζ в относитель­ном движении тела по отношению к центру масс (ось ζ проходит через центр масс тела перпендикулярно чертежу); - главный мо­мент внешних сил, приложенных к телу, относительно той же оси ζ.

Так как относительное движение тела по отношению к центру масс, т. е. по отношению к подвижной системе осей Сξηζ , является вращением вокруг оси ζ, то кинетический момент определяется по формуле (8.1):

.

Дифференцируем по t:

.

Подставляем это значение в уравнение:

.

Таким образом, дифференциальные уравнения плоского движения твердого тела имеют следующий вид:

. (8.3)

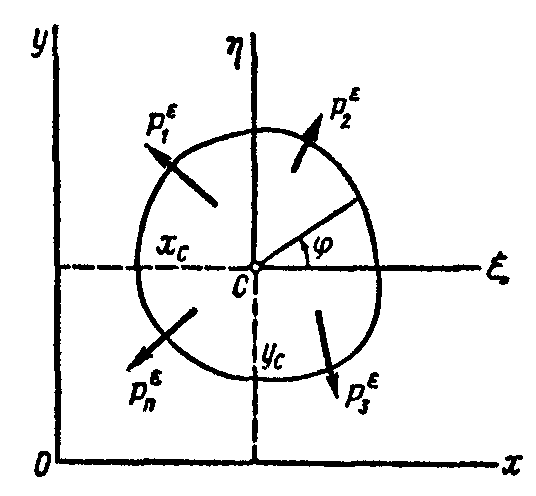
Рис. 8.3

Интегрируя эти уравнения, можно определить x_C, у_C , z_C как функции времени. Для определения шести постоянных интегрирования используются начальные условия движения: координаты центра масс и угол поворота тела в начальный момент t_o= 0, а также проекции начальной скорости центра масс на оси координат и начальная угловая скорость тела .

При определении движения несвободного твердого тела наряду с задаваемыми внешними силами учитываются и неизвестные реакции связей. В этом случае для решения задачи используются дополнитель­ные уравнения, определяющие ограничения движения тела имеющимися связями.

В том случае, когда траектория центра масс задана, удобно поль­зоваться дифференциальными уравнениями движения точки С в проек­циях на касательную и главную нормаль к этой траектории.

Тогда дифференциальные уравнения плоского движения твердого тела имеют вид

. (8.4)

Здесь s_c - дуговая координата центра масс, v_c - его скорость и ρ - радиус кривизны его траектории.

Пример. Однородный цилиндр весом G и радиусом r катится без скольжения по наклонной плоскости, составляющей с горизонтом угол а. Коэффициент сцепления равен (рис. 8.4). Определить: 1) ускорение движения центра масс цилиндра и 2) угол наклона плоскости, при котором начинается скольжение цилиндра, без учета сопротивления качению.

Решение. Движение цилиндра совершается под действием трех внешних: силы тяжести , нормальной реакции плоскости и силы сцепления . Направим оси х и у, как указано на рисунке. Через центр масс цилиндра С проведем оси ξ и η и ось ζ, перпендикулярную плоскости чертежа и направленную вверх. Момент силы относительно оси Сζ будет положителен, если сила стремится вращать плоскость чертежа вокруг точки С в направлении против вращения часовой стрелки, и отрицателен - в противоположном случае.

Составим дифференциальные уравнения (8.3) плоского движения тела:

, (а)

, (б)

. (в)

Так как за рассматриваемый промежуток времени , то , а потому из уравнения (б)

, откуда .

Дифференциальные уравнения (а) и (в) содержат три неизвестные вели­чины: и . Для определения этих неизвестных к двум составленным уравнениям добавим еще одно.

Так как цилиндр катится без скольжения, то точка Р соприкасания среднего сечения цилиндра с плоскостью является мгновенным центром скоростей среднего сечения. Поэтому

. (г)

Проекция скорости точки С на ось х: .

Алгебраическая величина угловой ско­рости отрицательна, так как цилиндр вращается по вращению часовой стрелки, т. е. , где |ω| — абсолютное значение угловой ско­рости.

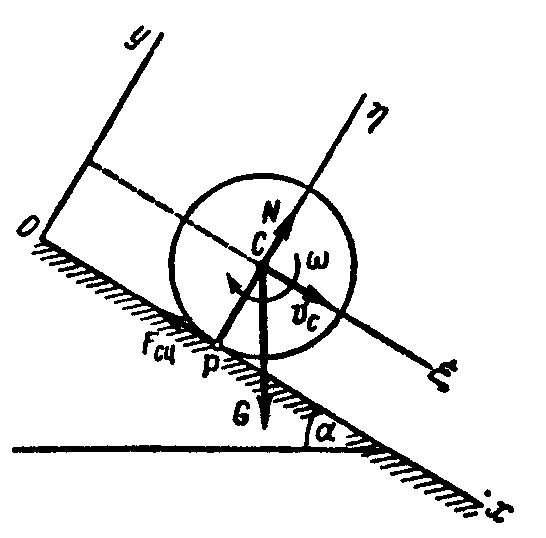
Рис. 8.4