Кинетический момент механической системы относительно центра о

. (7.11)

Кинетическим моментом (или главным моментом количеств дви­жения механической системы относительно оси) называется алгебра­ическая сумма моментов количеств движения всех материальных точек системы относительно этой оси.

Момент количества движения каждой точки системы (рис. 7.1, б) относительно оси Оz определяется согласно (7.3). Кинетический момент системы относительно оси (рис. 7.5) определяется по зависимости:

. (7.12)

Кинетические моменты механической системы относительно некоторого центра О и какой-либо оси z, проходящей через этот центр, связаны такой же зависимостью, как и главные моменты системы сил относительно центра и оси, т. е.

. (7.13)

Таким образом, проекция кинетического момента механической системы относительно некоторого центра О на ось, проходящую че­рез этот центр, равна кинетическому моменту системы относитель­но этой оси.

Теорема об изменения кинетического момента механической системы. Пусть система материальных точек , движется под действием некоторой системы сил, которые разделим на внешние силы и внутренние силы .

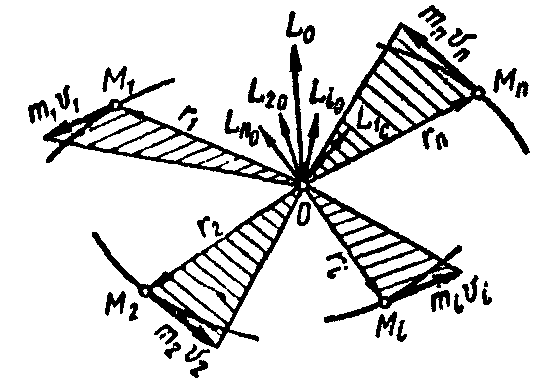
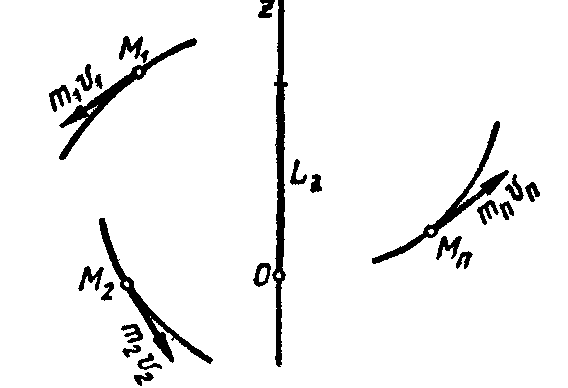
Рис. 7.4 Рис. 7.5

Выберем некоторый неподвижный центр О и определим изме­нение момента количества движения каждой точки относительно этого центра по уравнению (7.7):

.

Просуммируем полученные n уравнений:

. (a)

Как указывалось ранее, геометрическая сумма моментов всех внутренних сил относительно любого центра равна нулю, т. е. . Преобразуем левую часть равенства (а), учитывая (7.11):

.

Тогда уравнение (а) принимает вид

. (7.14)

Уравнение (7.14) выражает теорему об изменении кинетического момента механической системы: производная по времени от кинети­ческого момента механической системы относительно некоторого неподвижного центра геометрически равна главному моменту внешних сил, действующих на эту систему относительно того же центра.

Векторному равенству (7.14) соответствуют три равенства в про­екциях на оси координат:

(7.15)

Здесь согласно (7.13) — кинетические моменты механи­ческой системы относительно осей координат, а — главные моменты внешних сил относительно этих осей.

Уравнения (7.15) показывают, что производная по времени от кинетического момента механической системы относительно некоторой оси равна главному моменту внешних сил относительно этой оси.

Следствия из теоремы. 1. Если главный момент внешних сил относительно некоторого неподвижного центра остается все время равным нулю, то кинетический момент механической системы относительно этого центра остается постоянным.

Из уравнения (7.14) следует, что если , то

. (7.16)

2. Если главный момент внешних сил относительно некоторой оси остается все время равным нулю, то кинетический момент механической системы относительно этой оси остается постоянным.

Из уравнения (7.15) следует, что если, например, , то

. (7.17)

Следствия из теоремы об изменении кинетического момента меха­нической системы выражают закон сохранения кинетического момента механической системы.

Пример. Шарик М привязан к нити МВА, часть ВА которой продета сквозь вертикальную трубку (рис. 7.6). В момент, когда шарик находится на расстоянии от оси z трубки, ему сообщают начальную скорость , перпендикулярную плоскости МВА. Одновременно нить начинают медленно втягивать в трубку. Найти, какую скорость будет иметь шарик, когда его расстояние от оси z станет равно .

Рис. 7.6

Решение. На шарик действуют сила тяжести и реакция нити . Моменты этих сил относительно оси z равны нулю, так как сила параллельна оси z, а сила эту ось пересекает. Тогда по уравнению теоремы моментов относительно центра

находим

,

откуда . Так как масса т постоянна, то отсюда следует, что при движении шарика . Следовательно,

.

По мере приближения шарика к оси его скорость растет.

Лекция 8

ДИНАМИКА ВРАЩАТЕЛЬНОГО

ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА

1. Дифференциальное уравнение вращения твердого

тела вокруг неподвижной оси

Рассмотрим твердое тело, вращающееся вокруг неподвижной оси z с угловой скоростью ω (рис. 8.1). Вычислим кинетический момент этого тела относительно оси его вращения. Момент количества дви­жения точки M_i тела относительно оси z:

. (а)

где r_i - радиус окружности, описываемой точкой М_i; v_i= r_iω - алгеб­раическая величина вращательной скорости точки М_i. Подставляя в (а) это значение v_i, получаем

.

Кинетический момент твердого тела относительно оси z

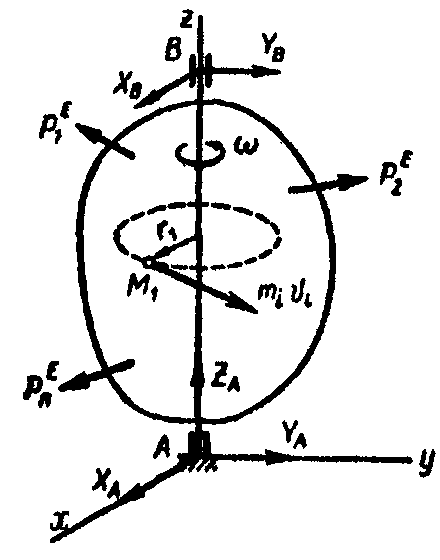
Рис. 8.1

Здесь - момент инерции твер­дого тела относительно оси z.

Таким образом,

, (8.1)

т. е. кинетический момент вращающегося твердого тела относительно неподвижной оси его вращения равен произведению момен­та инерции тела относительно той же оси на угловую скорость тела.

Рассмотрим изменение кинетического момента тела относительно оси z под действием приложенных к нему задаваемых внеш­них сил . Теорема об изме­нении кинетического момента механической системы выражается урав­нением:

.

Реакции подшипника В и подпятника А являются внешними си­лами, но при отсутствии трения их моменты относительно оси z равны нулю и правая часть уравнения содержит только сумму момен­тов задаваемых внешних сил. При наличии трения эта сумма содер­жит также момент сил трения. Так как по (8.1)

,

то

,

а потому уравнение принимает вид

. (8.2)

Уравнение (8.2) представляет собой дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.

Сравним уравнение (8.2) с дифференциальным уравнением посту­пательного прямолинейного движения твердого тела:

.

Очевидно, что момент инерции твердого тела при вращательном движении имеет то же значение, что и масса тела при его поступа­тельном движении: момент инерции является характеристикой инерт­ности тела при вращательном движении.

Если вращение тела происходит в одном направлении, то это направление считают положительным. В этом случае моменты движу­щих сил положительны, моменты сил сопротивления отрицательны, а главный момент внешних сил может иметь тот или другой знак. Если , т.е. тело вращается ускоренно. Если , т. е. вращение тела равномерное (по инерции). Если , т. е. тело вращается замед­ленно.

По дифференциальному уравнению (8.2) можно решать следующие задачи:

- по заданному уравнению вращения тела φ=f(t) и его моменту инерции J_z определять главный момент внешних сил, действующих на тело:

;

- по заданным внешним силам, приложенным к телу, по началь­ным условиям вращения φ_о и ω_о и по моменту инерции тела J_z находить уравнение вращения тела φ=f(t);

3) определять момент инерции тела J_z относительно оси вращения, зная величины и .

Пример. Натяжения ветвей ремня, приводящего во вращение шкив, равны 20 и 40 Н. Шкив имеет вес 80 Н, радиус 30 см и радиус инерции относительно оси вращения 25 см. Составить уравнение вращения шкива из состояния покоя, пренебрегая трением.

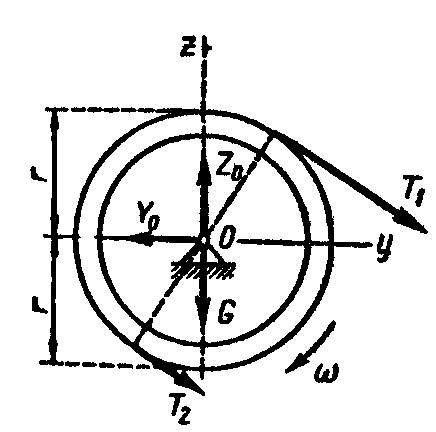
Рис. 8.2

Решение. Дифференциальное уравнение вращения шкива вокруг непод­вижной оси Ох (рис. 8.2) имеет вид (8.2):

.

К шкиву приложены внешние силы: реакции ветвей ремня и , вес шкива и составляющие реакции опоры и .

Направление вращения тела принимают всегда за положительное. Тогда моменты сил, направленных в сторону вращения, положительны, а моменты сил, направленных противоположно, отрицательны. Главный момент внешних сил

(моменты сил , , относительно оси Ох равны нулю). Момент инерции шкива определяем по радиусу инерции:

Подставляем числовые значения J_x и в уравнение (8.2): Отсюда находим угловое ускорение:

.

Интегрируем дважды по t: .

По начальным условиям находим С₁ = 0 и C₂=0. Таким образом, уравнение вращения шкива имеет вид

.