Пользуясь этими выражениями, получаем

.

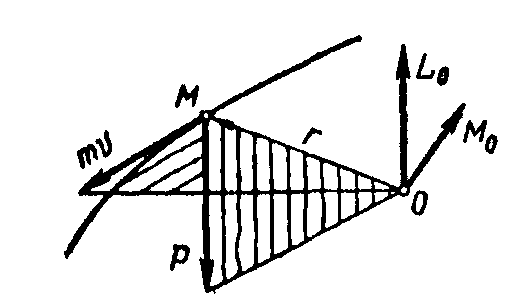
Рис. 7.2

Так как угол то

,

тогда

,

или

. (7.6)

Если на материальную точку действует несколько сил, то следует рассматривать как момент их равнодействующей. Заменим геоме­трической суммой моментов составляющих сил:

или

. (7.7)

Соотношение (7.7) выражает теорему об изменении момента коли­чества движения материальной точки относительно центра: производная по времени от момента количества движения материальной точки относительно некоторого неподвижного центра равна геометри­ческой сумме моментов сил, действующих на точку, относительно того же центра.

Так как проекция векторной производной на любую ось равна про­изводной от ее проекции на эту ось, то, проецируя векторное равенство (7.7) на оси x,y,z, получим три равенства:

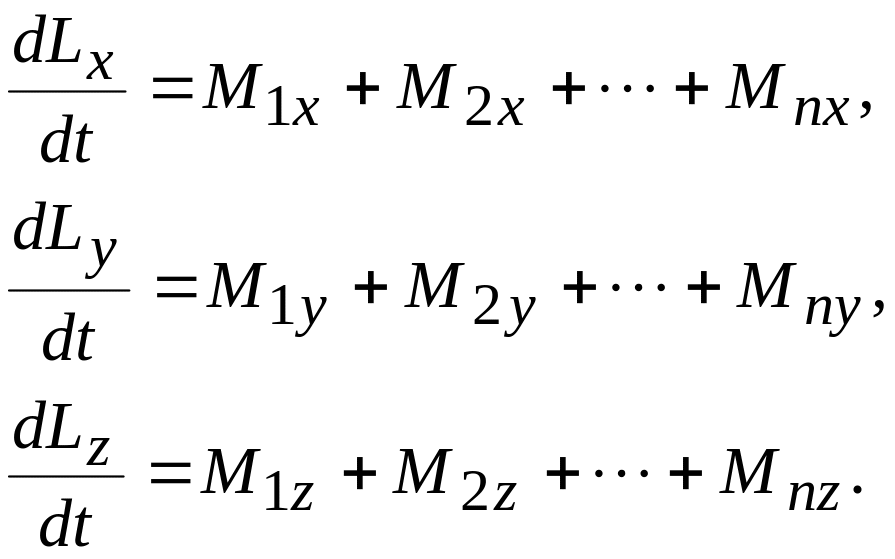
или

(7.8)

Здесь согласно (7.8) - моменты количества движения точки М относительно осей координат, а - моменты силы относительно этих же осей.

Равенства (7.8) выражают теорему об изменении момента коли­чества движения точки относительно оси: производная по времени от момента количества движения материальной точки относительно некоторой неподвижной оси равна алгебраической сумме моментов сил, действующих на точку, относительно этой же оси.

Следствия из теоремы: 1. Если линия действия равнодействующей приложенных к материальной точке сил все время проходит через некоторый неподвижный центр, то момент количества движения материальной точки относительно этого центра остается постоянным.

Из уравнения (7.7) следует, что если

,

то

. (7.9)

Примером, иллюстрирующим это следствие, может служить дви­жение материальной точки под действием центральной силы.

Центральной называется сила, линия действия которой за время движении проходит через некоторый центр, а модуль за­висит от расстояния между этим центром и точкой приложения силы.

Положим, что линия действия центральной силы за время дви­жения проходит через центр С (рис. 7.3). Тогда

.

Из этого следует, что плоскость, проходящая через вектор ко­личества движения точки и центр С, не изменяет своего положения, т. е. траектория точки лежит в одной плоскости.

2. Если момент равнодействующей приложенных к материальной точке сил относительно некоторой оси все время равен нулю, то момент количества движения материальной точки относительно этой оси остается постоянным.

Из уравнения (7.8) следует, что если, например, , то

. (7.10)

2. Теорема об изменении кинетического момента механической системы относительно центра и оси

Кинетический момент механической системы относительно центра и оси. Кинетическим моментом (или главным моментом количеств движения механической системы относительно данного центра) называют вектор, равный геометрической сумме моментов количеств движения всех материальных точек системы относительно этого центра.

Момент количества движения каждой материальной точки системы (рис. 7.4) относительно центра О определяется по формуле (7.2):

.