
- •Конспект лекций
- •Введение. Понятие о численных методах. История развития численных методов.
- •Интерполяция функций.
- •Постановка задачи.
- •Конечные разности различных порядков.
- •Диагональная таблица
- •Первая интерполяционная формула Ньютона.
- •Горизонтальная таблица разностей.
- •Вторая интерполяционная формула Ньютона.
- •Горизонтальная таблица разностей.
- •Общая характеристика интерполяционных формул с постоянным шагом.
- •Интерполяционная формула Лагранжа.
- •Частные случаи.
- •Формула Ньютона для неравностоящих узлов Разделённые разности
- •Интерполяционная формула Ньютона для неравностоящих значений аргумента
- •Погрешность формулы Ньютона для неравностоящих узлов
- •Интерполяция сплайками
- •Многочлены Чебышева
- •Выбор узлов интерполирования
- •Обратное интерполирование для равноотстоящих узлов
- •Обратное интерполирование для неравноотстоящих точек
- •Общие выводы по задаче интерполяции
- •Оценка погрешности интерполяционной формулы Лагранжа
- •Решение системы линейных уравнений Общая характеристика методов решения систем линейных уравнений
- •Прямой метод
- •По правилу Крамера
- •Метод Гаусса. Схема единственного деления
- •Трудоёмкость метода Гаусса
- •Метод Гаусса. Схема с выбором главного элемента
- •Достоинства метода
- •Метод итераций
- •Сходимость метода итераций для решения системы алгебраических уравнений
- •Достоинства метода итераций
- •Метод Зейделя
- •Численное решение систем нелинейных уравнений Постановка задачи
- •Метод Ньютона
- •Сходимость метода Ньютона
- •Теорема о существовании корней и сходимости процесса Ньютона
- •Градиент функции u
- •1 Итерация
- •2 Итерация
- •Сходимость градиентного метода
- •Численное решение обыкновенных дифференциальных уравнений
- •Численные методы решения обыкновенных дифференциальных уравнений. Метод Эйлера.
- •Особенности метода Эйлера.
- •Первая улучшенная формула Эйлера
- •Вторая улучшенная формула Эйлера
- •Метод Рунге-Кутта.
- •Методы обработки экспериментальных данных. Постановка задачи
- •Узловые точки
- •Класс функций
- •Критерий согласия
- •Среднеквадратичный критерий
- •Минимаксный критерий или критерий чебышева
- •Линейная функция.
- •Квадратный трехчлен.
- •Степенная функция
- •Показательная функция.
- •Логарифмическая функция.
- •Дробно-линейная функция.
- •Гипербола.
- •Дробно-рациональная.
Достоинства метода
Если матрица вырождения, то перед исключением неизвестной главный элемент считается равным нулю =>
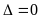
С помощью метода Гаусса можно вычислить определитель
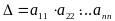 треугольной матрицы.
треугольной матрицы.
При большом числе неизвестных схема метода Гаусса, дающая точное решение, становится весьма сложной.
В этих случаях для нахождения корней системы лучше пользоваться приближёнными численными методами.
Метод итераций
Дана система уравнений
Можно привести
систему к такому виду, чтобы диагональные
элементы были отличные от нуля, то есть
![]() ,
тогда разрешая
-тое
уравнение относительно
,
получаем
,
тогда разрешая
-тое
уравнение относительно
,
получаем
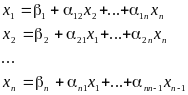 ,
(2)
,
(2)
где
![]() ,
,
![]() ,
,
![]() или
или
![]() при
при
![]()
 ,
,
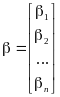 .
.
Тогда систему уравнений 2 можно записать в виде:
![]() - итерационная
формула.
- итерационная
формула.
Таким образом,
выбрав начальные значения
![]()
![]()
и так далее.
Итерации
останавливаются, когда
![]() ,
,
![]()
![]()
Сходимость метода итераций для решения системы алгебраических уравнений
Теорема:
Система уравнений имеет единственное
решение и сходится при любом начальном
значении
![]() тогда и только тогда, когда все собственные
значения матрицы
тогда и только тогда, когда все собственные
значения матрицы
![]() по модулю меньше 1.
по модулю меньше 1.
Если для системы уравнений
выполнено хотя бы одно из условий:
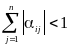 ,
,
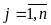
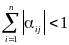 ,
,
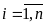
то процесс итерации сходится, независимо от выбора начального условия.
Однако этой теоремой в общем случае очень тяжело воспользоваться, поэтому на практике пользуются другим правилом менее жёстким.
Если эти условия выполняются, то в принципе логично выбрать для начальных значений. На практике в качестве начального приближения используют вектор свободных членов.
Приведение линейной системы к виду, удобному для итерациию.
Теорема сходимости накладывает жёсткие условия к коэффициентам данной линейной системы.
Однако, если
![]() ,
то эту систему всегда можно привести к
такому виду:
,
то эту систему всегда можно привести к
такому виду:
![]() ,
чтобы удовлетворить условиям 1
,
чтобы удовлетворить условиям 1
Первый способ.
Дано:
Домножим это
уравнение на матрицу
![]() ,
где
,
где
![]()
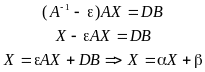 ,
,
где
![]()
Второй способ.
Каждое
-ое
уравнение делится на
![]()
![]()
Тогда
,
,
![]() .
.
Тогда уравнение сходимости имеет вид
![]() ,
,
![]() ,
,
Эти неравенствабудут выполняться, если диагональные элементы будут удовлетворять условиям:
![]() ,
,
,
,
то есть если модули диагональных коэффициентов для которого уравнения системы больше суммы модулей всех остальных коэффициентов.
Достоинства метода итераций
Если итерации сходятся быстро, то есть для сходимости требуется менее итераций, то выигрыш во времени по сравнению с методом Гаусса:
![]() ,
,
![]() -
число итераций
-
число итераций
![]()
Погрешности округления в методе итераций сказывается значительно меньше, чем в методе Гаусса. Кроме того, метод итерации является самоисправляющимся, то есть отдельная ошибка запрещается в вычислениях, не отражаясь на конечном результате, то есть ошибочное приближение можно рассматривать как новый начальный вектор.
Метод итераций становится особенно выгодным при решении систем, у которых значительное число коэффициентов равно нулю.
Метод итераций легко программируется.
Метод Зейделя
Является модификацией
метода итераций. Основная идея заключается
в том, что при вычислении
![]() -го
приближения
-го
корня используются уже вычисленные
приближённые корни
-го
приближения
-го
корня используются уже вычисленные
приближённые корни
![]() .
.
Дано:
![]() ,
,
Выбираем начальное приближение:
![]()
На
![]() -том
шаге, согласно Зейделю строим приближение
по следующим формулам:
-том
шаге, согласно Зейделю строим приближение
по следующим формулам:
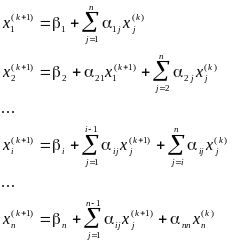
Метод Зейделя даёт полную сходимость по сравнению с методом итерации, но приводящий к громоздким вычислениям.
Теорема: Для существования единственного решения системы сходимости метода Зейделя достаточно выполнение хотя бы одного из двух условий:
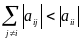 ,
,
матрица - симметричная положительно определённая (все её соответственно значения положительны)
