
- •24. Класи інтегровних функцій.
- •25.Властивості означених інтегралів
- •26. Інтеграл зі змінною верхньою межею, властивості. Формула Ньютона-Лейбніца.
- •27. Застосування означеного інтеграла(обчислення площ, об’єму тіла, довжини кривої)
- •27. Застосування означеного інтеграла(обчислення площ, об’єму тіла, довжини кривої)
- •28. Невласні інтеграли 1 і 2 роду. Критерій збіжності. Достатні умови
- •28. Невласні інтеграли 1 і 2 роду. Критерій збіжності. Достатні умови
- •29. Екстремум функції багатьох змінних. Необхідна умова. Достатні умови екстремуму
- •29. Екстремум функції багатьох змінних. Необхідна умова. Достатні умови екстремуму
24. Класи інтегровних функцій.
1)Неперерв.
на
![]() ф-ції ; f(x)
ф-ції ; f(x)![]() C[a,b]
C[a,b]
Доведення.
Перевір. необх. і дост.умови
![]()
![]() Рімана.
Рімана.
![]() .
.
![]() =max
=max![]() x
x![]() 0
0![]()
(1’)
![]() ;
(1’) на
мові
;
(1’) на
мові
![]() звучить
так: Щоб
f(x)
була
інтегрована за Ріманом на f(x)
звучить
так: Щоб
f(x)
була
інтегрована за Ріманом на f(x)![]() необх.
і дост.,щоб для
необх.
і дост.,щоб для
![]() >0,
>0,![]() ,що
як тільки
,що
як тільки
![]() 0
0![]() (*)-це
необ. дост.умова. w
=
(*)-це
необ. дост.умова. w
=![]() ;w
-коливання.
;w
-коливання.
x![]() ,
f(x)
,
f(x)![]()
m
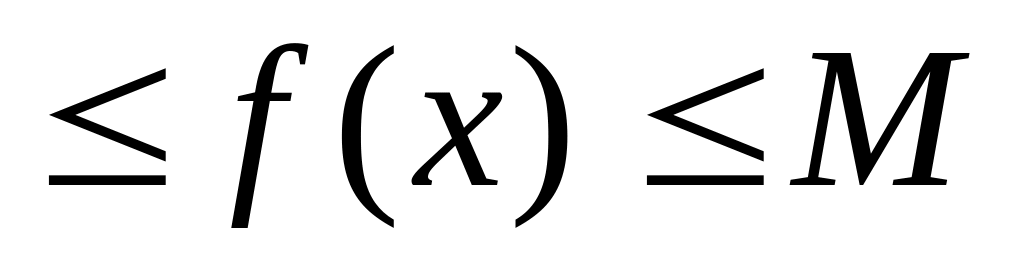
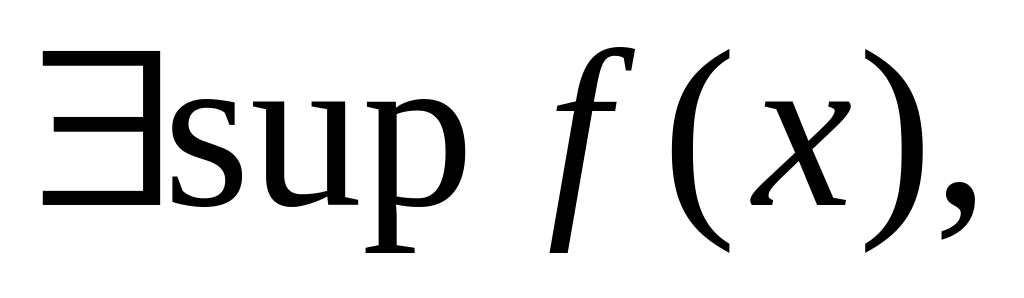
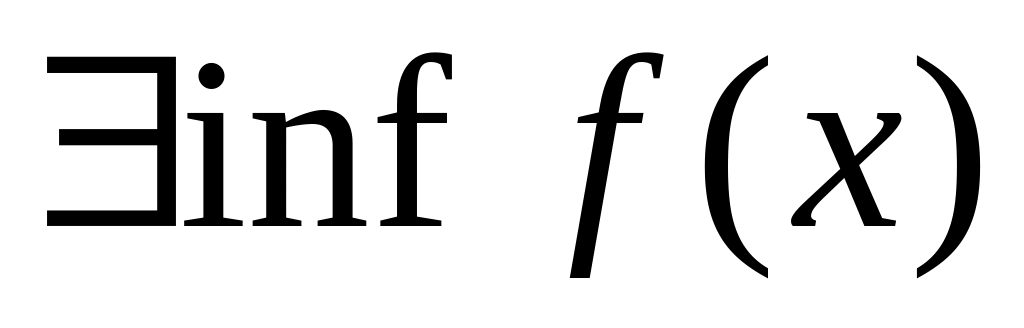 в
точ.x
в
точ.x і
x
і
x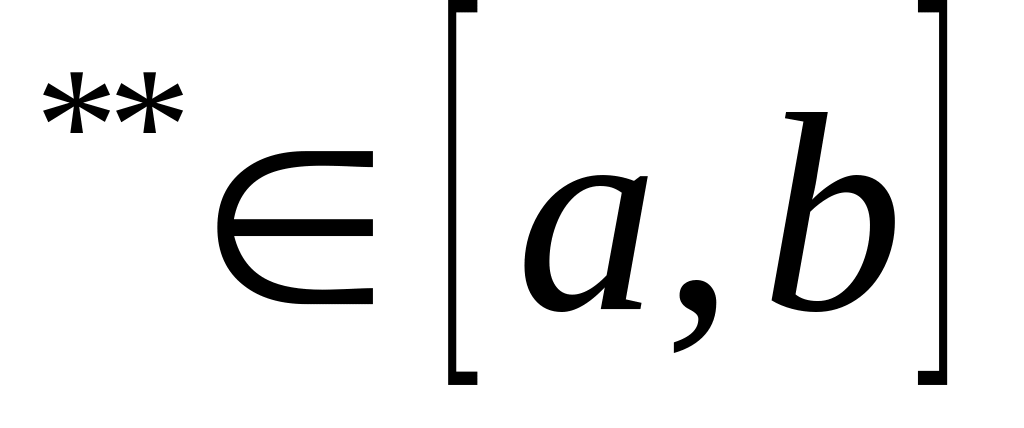
Якщо f(x) непер. на ,то вона рівномір. непер.
Наслідок:
Якщо
f(x)![]() ,що
якщо розбити відрізок
на частин.<
,що
якщо розбити відрізок
на частин.<![]() ,
то коливання w
<
,
то коливання w
<![]() .
Цей наслідок використ.для доведення.
.
Цей наслідок використ.для доведення.
>0,
![]() >0,
>0,
![]() <
,
тобто
max
<
,
тобто
max![]() <
<![]() <
<![]() ,
,
![]() <
<![]()
Ми одержали (*),а це необх. і дост. у.,щоб ф-ція була інтегрована.
2клас.f(x),
x![]() і
монотонна. Монотон.ф-ції можуть мати
скінч.або злічен.кількість розривів І
роду,тому це не підходить до 1-го класу.
і
монотонна. Монотон.ф-ції можуть мати
скінч.або злічен.кількість розривів І
роду,тому це не підходить до 1-го класу.
А)неспадна:
перевір. викон.умови (*).
розіб’єм
на частини. a=x![]() <…<x
<…<x![]()
w![]() ;
;
![]() (2);
>0,
0<
(2);
>0,
0<![]() <
<![]()
![]() <
(3) В
(3) підстав. (2).
<
(3) В
(3) підстав. (2).
<![]()
<
3 клас
f(x),
x
,
неперерв.за
винятком скінч.кільк.точок в яких є
розрив І роду.В x![]() ф-ція f(x)
має
стрибки,а для точ.x
ф-ція f(x)
має
стрибки,а для точ.x![]() ,
i=1…k
f(x)-непер.Покажемо,що
f(x)
інтегр. на
.
<
,
(x
,
i=1…k
f(x)-непер.Покажемо,що
f(x)
інтегр. на
.
<
,
(x![]() <
;
<
;
![]() ,
…,
,
…,![]() -на
цих відрізках ф-ція непер.і на кож.відрізку
викон.наслідок зтеор. Кантора,то по
>0,
-на
цих відрізках ф-ція непер.і на кож.відрізку
викон.наслідок зтеор. Кантора,то по
>0,
![]() >0,що
коли розбити на частини j-відрізок
<
,то
w
<
;
min
>0,що
коли розбити на частини j-відрізок
<
,то
w
<
;
min![]() і
зробимо розбиття
на частини,де
і
зробимо розбиття
на частини,де
< Може бути,що частинки лежать в -околі точки,тому:
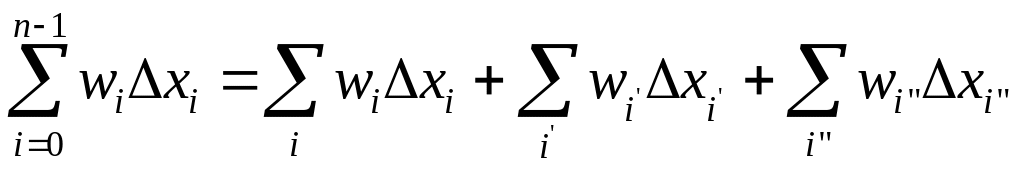 В
цих сумах не викон.наслідок теореми
Кантора,тому w
В
цих сумах не викон.наслідок теореми
Кантора,тому w![]() замінимо
на
замінимо
на
![]() -коливання,
f(x)
на
.
-коливання,
f(x)
на
.
![]() <2
<2![]()
![]() <
<![]() <
<![]() ;
(
;
(![]() <
<![]() ;
<
;
<![]() ;
w
<
;
w
<![]() ;
;
![]() <
<![]() і
буде виконуватись
і
буде виконуватись
(*) Ми виділили 3 основні класи ф-цій,які є інтегровані.
25.Властивості означених інтегралів
1. ![]()
2. Якщо
функція f
інтегровна
на відрізку [a,b],
то
вона інтегровна на будь-якому відрізку
[a*,b*]![]() [a,b].
[a,b].
3. Нехай
a![]() c
b.
Якщо функція f
інтегровна на відрізках [a,с]
і [с,b],
то функція f
інтегровна і на відрізку [a,b],
причому
c
b.
Якщо функція f
інтегровна на відрізках [a,с]
і [с,b],
то функція f
інтегровна і на відрізку [a,b],
причому ![]() =
=![]() +
+![]() .
.
4. Якщо
функції f
і
g
інтегровні на відрізку [a,b],
то їх сума f+g
теж інтегровна на цьому відрізку і
![]() =
+
=
+![]() .
.
5. Нехай
функція f
інтегровна на відрізку [a,b],
і c
– стала, тоді функція cf
теж інтегровна на цьому відрізку і
![]() =с
=с![]()
6. Нехай функції f(x) i g(x) інтегровні на відрізку [a,b], тоді їх добуток f(x)g(x) теж інтегровний на цьому відрізку.
7. Якщо
функція f
невід’ємна
і інтегровна на відрізку [a,b],
то ![]() 0.
0.
8. Якщо
функції f
і
g
невід’ємні
і інтегровні на відрізку [a,b]
і для всіх [a,b],
то ![]() .
.
9.
Для будь-якої функції f
покладемо
за означенням ![]() ,
а
для функції f
інтегровної
на відрізку [a,b],
,
а
для функції f
інтегровної
на відрізку [a,b],
![]() –
,
a<b.
–
,
a<b.
10.
Якщо функція f
інтегровна
на відрізку [a,b],
то і функція |f|
теж
інтегровна на цьому відрізку і ![]() ,
a<b.
,
a<b.
26. Інтеграл зі змінною верхньою межею, властивості. Формула Ньютона-Лейбніца.
Якщо
функція f(x)
інтегровна в проміжку [a,
b]
(a≷b),
то вона інтегровна і на проміжку [a,
x],
де x
є довільне значення з [a,
b].
Замінивши границю b
визначеного інтеграла змінною х,
отримаємо вираз
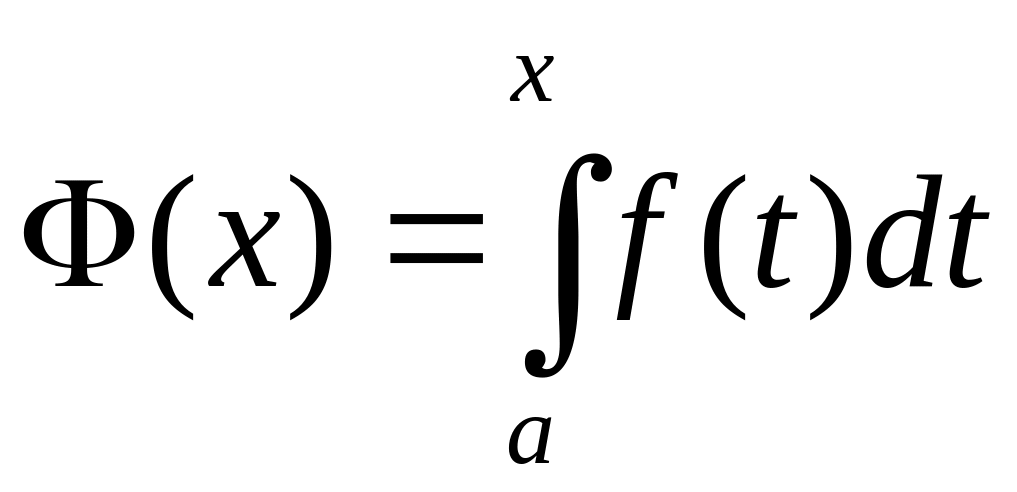 ,
(1) який є функцією від х. Ця функція
називається інтегралом зі змінною
верхньою межею і має такі властивості:
,
(1) який є функцією від х. Ця функція
називається інтегралом зі змінною
верхньою межею і має такі властивості:
Якщо функція f(x) інтегрована на [a, b], то
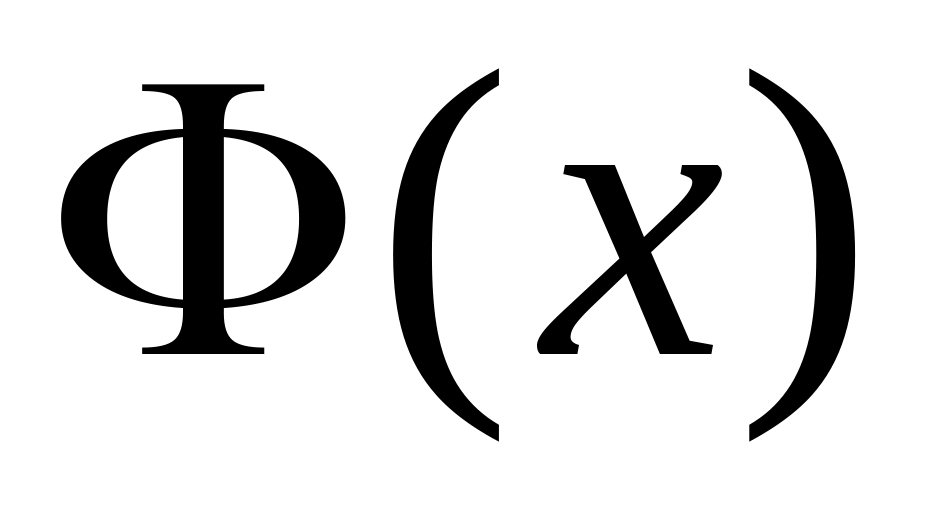 буде
неперервною функцією від х в тому ж
проміжку.
буде
неперервною функцією від х в тому ж
проміжку.
Доведення.
Оскільки f
інтегрована на [a,
b],
то f
обмежена, тобто існує M>0:
|f(x)|≤M.
Нехай x![]() [a,
b]
і x+
[a,
b]
і x+![]() x
[a,
b],
x
[a,
b],
![]() .
Функція
.
Функція
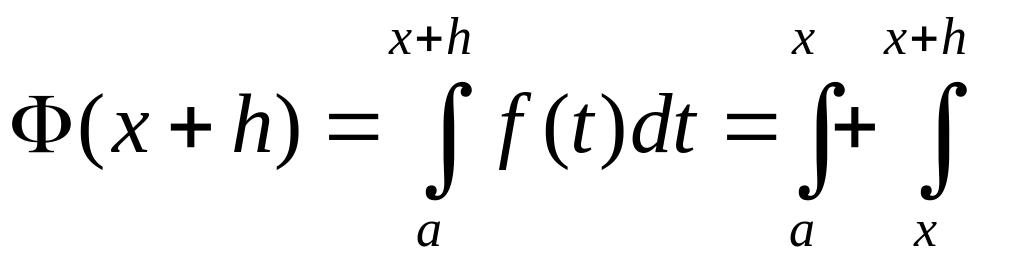 ,
тоді
,
тоді
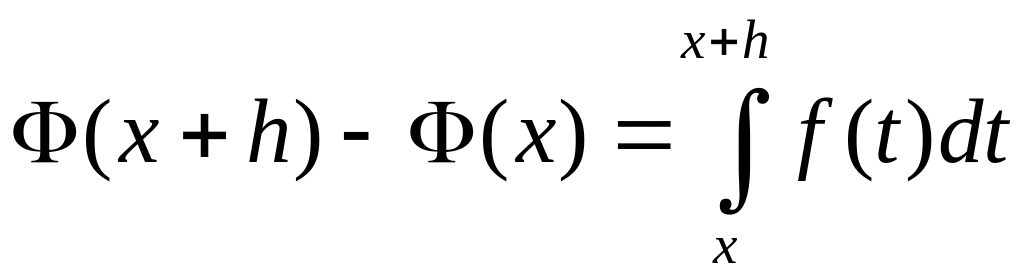 .
Застосувавши до цього інтегралу теорему
про середнє значення
.
Застосувавши до цього інтегралу теорему
про середнє значення
![]() ;
(2) тут
;
(2) тут
![]() міститься між точними границями
міститься між точними границями
![]() функції f(x)
в проміжку [x,
x+h],
а отже, тим більше між (постійними) її
границями
функції f(x)
в проміжку [x,
x+h],
а отже, тим більше між (постійними) її
границями
![]() в основному проміжку [a,
b].
Якщо спрямувати тепер h
до нуля, то, очевидно
в основному проміжку [a,
b].
Якщо спрямувати тепер h
до нуля, то, очевидно
![]() або
або
![]() ,
що й доказує неперервність функції
.
,
що й доказує неперервність функції
.
Якщо припустити, що функція f(t) неперервна в точці t=x, то в цій точці функція
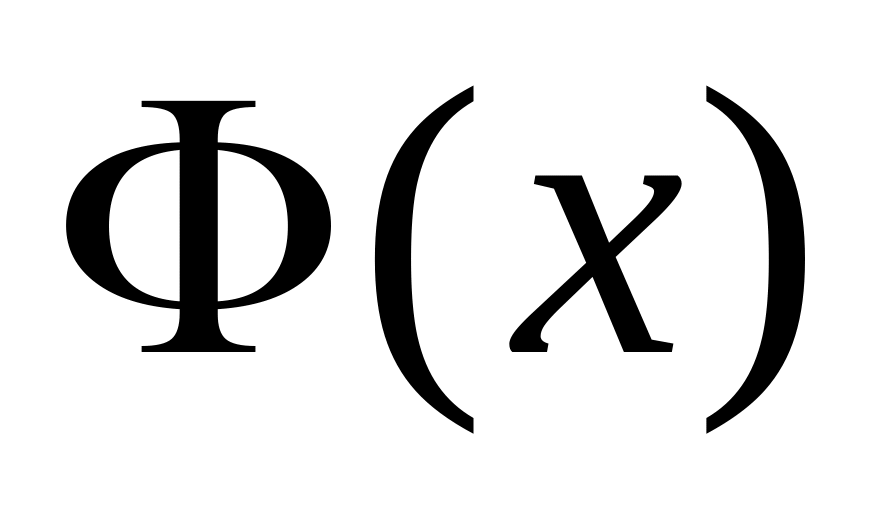 має похідну, яка дорівнює f(x),
тобто
має похідну, яка дорівнює f(x),
тобто
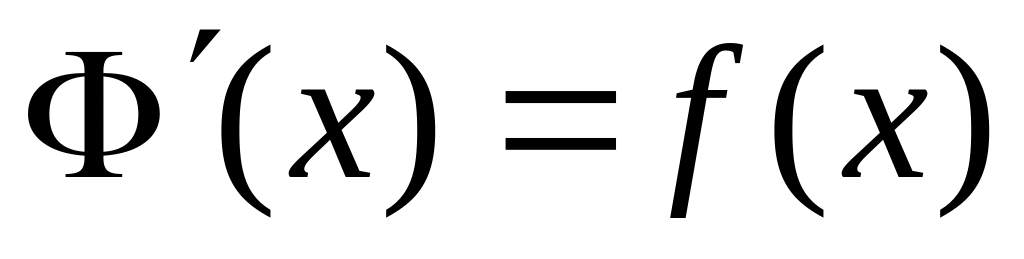 .
.
Доведення.
Дійсно, із (2) маємо
![]() ,
або
,
або
![]() .
Але,
зважаючи на неперервність функції
f(t)
при t=x,
для будь-якого
.
Але,
зважаючи на неперервність функції
f(t)
при t=x,
для будь-якого
![]() знайдеться таке
знайдеться таке
![]() ,
що при
,
що при
![]()
![]() для всіх значень t
в проміжку
[x,
x+h].
В такому випадку виконуються нерівності
для всіх значень t
в проміжку
[x,
x+h].
В такому випадку виконуються нерівності
![]() ,
так що
,
так що
![]() .
Отже,
.
Отже,
![]() ,
що й треба було довести.
,
що й треба було довести.
Ми прийшли до такого висновку: для неперервної в проміжку [a, b] функції f(x) завжди існує похідна; прикладом її є визначений інтеграл (1) зі змінною верхньою межею.
Основна формула інтегрального числення (Формула Ньютона-Лейбніца).
Для
неперервної в проміжку [a,
b]
функції f(x)
інтеграл (1) є первісною функцією. Якщо
F(х)
є довільна первісна для f(x)
функція, то
![]() .
Сталу С
можна
визначити, поклавши тут х=а, бо
.
Сталу С
можна
визначити, поклавши тут х=а, бо
![]() ;
будемо мати
;
будемо мати
![]() ,
звідси
,
звідси
![]() .
Отже,
.
Отже,
![]() .
Зокрема, при х =b
отримаємо
.
Зокрема, при х =b
отримаємо
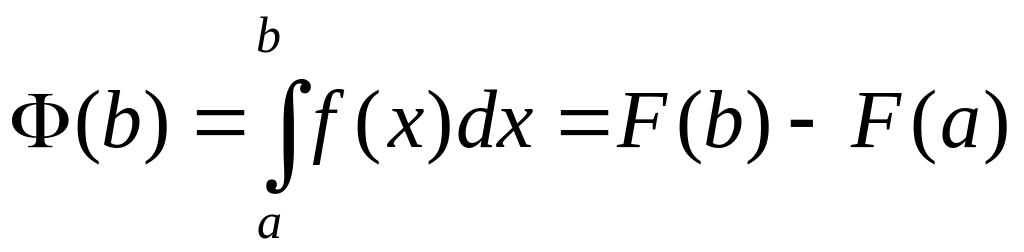 .
(А) – це основна формула інтегрального
числення.
.
(А) – це основна формула інтегрального
числення.
Отже, значення визначеного інтеграла визначається як різниці двох значень, при х =b і при x=a, будь-якої первісної функції.
Якщо
застосувати до інтегралу теорему про
середнє і згадати, що
![]() ,
то отримаємо
,
то отримаємо
![]() .
.
