6. Границя послідовності. Властивості збіжних послідовностей.

Нехай , . За теоремою 7 дістаємо, що , , тоді . Оскільки величина -- нескінчено мала, то . Звідси за теоремою 7 , або , що те саме,

Теорема 9. (про границю добутку). Якщо послідовності і ,то послідовність має границю, причому

Доведення аналогічне доведенню теореми 8.

Наслідок. Сталий множник можна виносити за знак границі.

Лема. Якщо послідовність , має границю, відмінну від нуля, то послідовність обмежена.

Теорема 10 (про границю частки). Якщо послідовності і , причому і всі , то границя частки існує і .

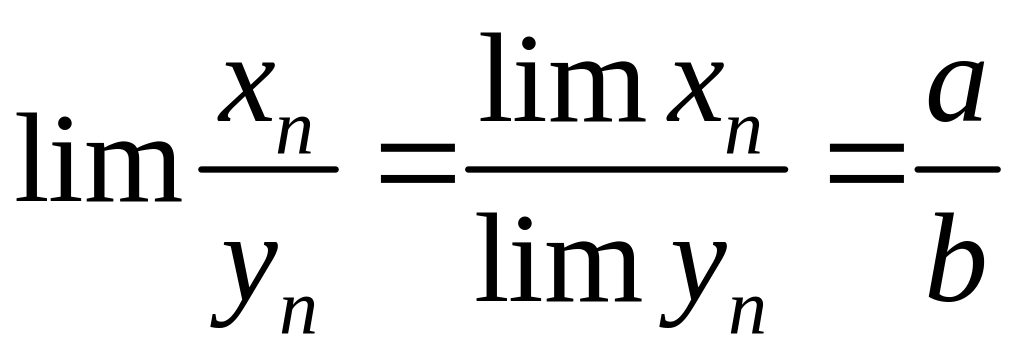Доведення.

З умов і маємо , , де , нескінченно малі, тоді

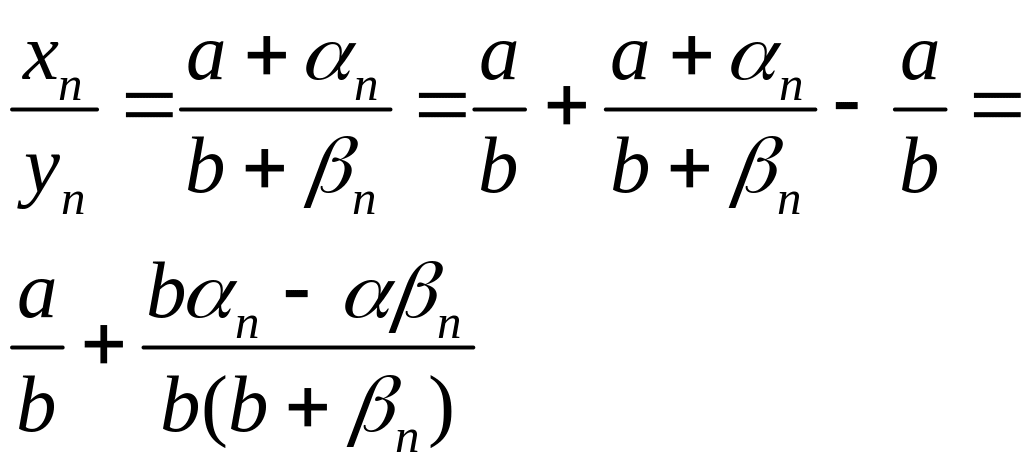. За властивостями нескінченно малих величин є нескінчено малою величиною. Тоді 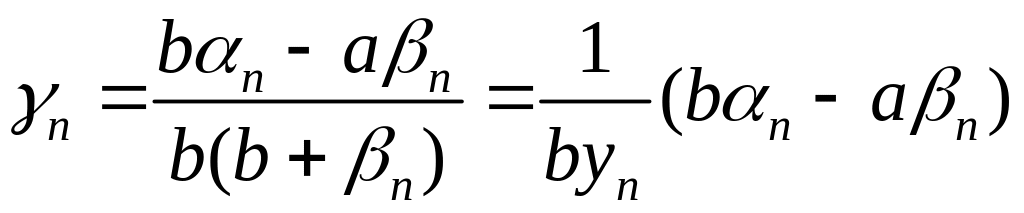-- нескінченно мала як добуток обмеженої та нескінченно малої послідовностей. Таким чином, 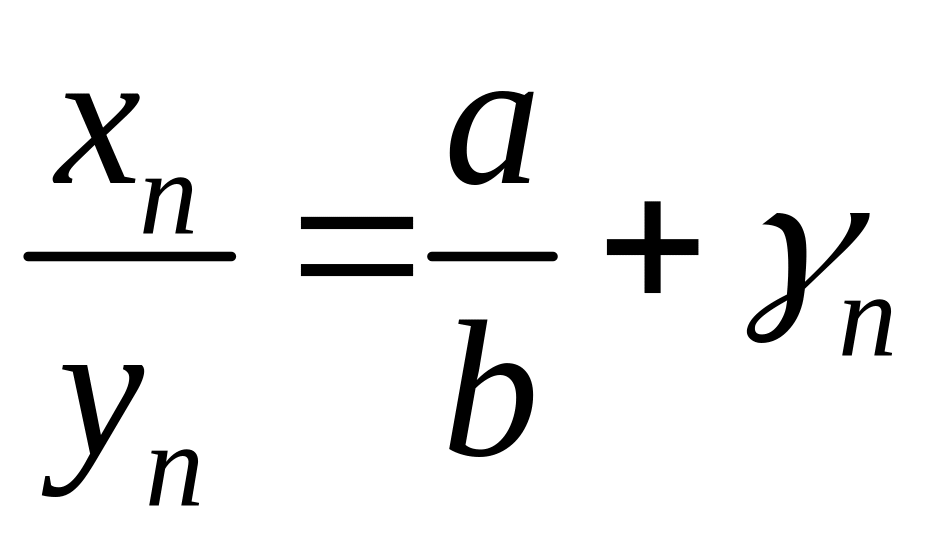, де -- нескінченно мала. Звідси маємо, що .

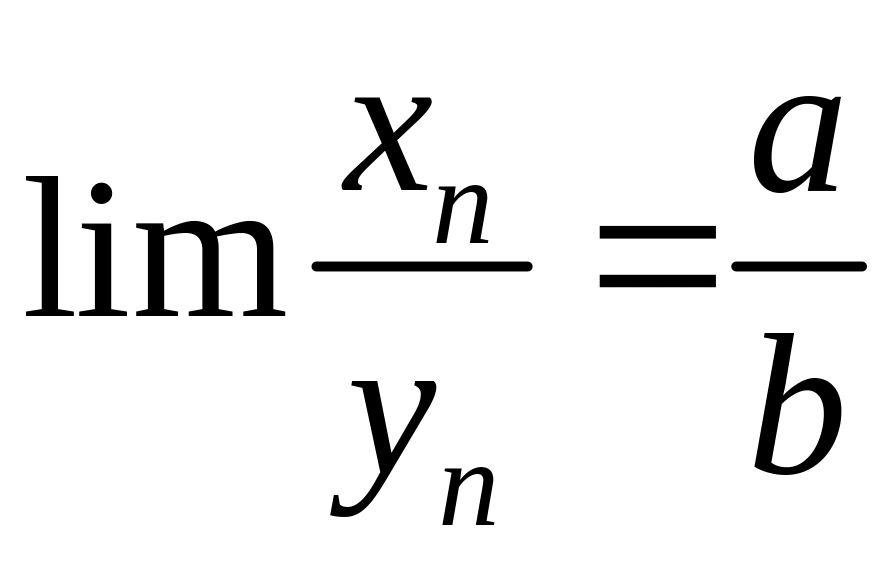7. Різні означення границі функції. Їх еквівалентність.

Нехай задана функція в області визначення X , і задана точка , яка може і не належати до області визначення.

Означення 1 "мовою послідовностей". Число називається границею функції в точці , якщо для всякої послідовності , що збігається до , відповідна послідовність значень функції збіжна до .

Означення 2 мовою " ". Число називається границею функції в точці , якщо для всякого існує таке , що з нерівності слідує нерівність .

Еквівалентність означень.

Нехай виконується означення 2, тобто для всякого існує таке , що з нерівності слідує нерівність . Оберемо з області значень функції послідовність . За означенням границі послідовності це означає, що для всякого існує , що з того що слідує , а згідно нашого припущення , буде вірною і така нерівність , а це й означає, що

Нехай виконується означення 1, тобто для всякої послідовності , що збігається до , відповідна послідовність значень функції збіжна до . Припустимо, що означення 2 не виконується, тоді існує таке , що . Виберемо такі що :

…………………………

…………………………

Нехай , тоді , а оскільки виконується означення 1, то це означає, що , а це протирічить тому, що .

Отже, наше припущення невірне.

Число називається границею функції в точці зліва (лівосторонньою), якщо для всякого існує таке , що з нерівності слідує нерівність .

Число називається границею функції в точці справа (правосторонньою), якщо для всякого існує таке , що з нерівності слідує нерівність .

Теорема. Щоб існувала границя функції в точці, необхідно і достатньо, щоб існували і були рівні односторонні границі.

8. Існування границі для монотонних послідовностей та функцій. Критерій існування

границі для послідовностей, функцій.

Теорема про існування границі монотонної послідовності.

I. 1) Якщо послідовність монотонно зростаюча можливо в широкому сенсі і обмежена зверху, то вона має скінчену границю .

2)Якщо послідовність монотонно зростаюча можливо в широкому сенсі і необмежена зверху, то .

II 1) Якщо послідовність монотонно спадна і обмежена знизу, то існує скінчена границя .

2) Якщо послідовність монотонно спадна і необмежена знизу, то .

Доведення.

I 1) Дано послідовність , яка зростаюча і обмежена зверху. Отже існує , що для всіх виконується , то ми маємо множину і вона обмежена зверху, то для неї існує верхня точна грань , . З властивості випливає: якщо ми візьмемо трохи менше число ніж , то знайдене з послідовності більше за число, яке менше за , тобто . Тоді знайдеться (*). Але для всіх номерів маємо , тоді . З другого боку для будь-якого . Ми маємо : , . Тобто , . Це означає, що є границею.

2) Послідовність зростаюча і необмежена зверху, тобто яке б ми не взяли (як завгодно велике), то знайдеться . Тепер використаємо зростання. Для всіх , . Це і означає, що .