2.3 Примеры решения обратной задачи

П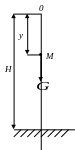 ример 1: сила постоянна по модулю и направлению. Свободное падение тела без учета сопротивления воздуха.

Рассмотрим движение тела М, падающего на поверхность земли с высоты Н, полагая вес тела G постоянным (рис.3). Пренебрегая размерами тела, будем считать его материальной точкой. Сначала рассмотрим падение тела в пустоте, без учета сопротивления воздуха.

1. Составляем основное уравнение динамики:

2

Рисунок 3

. Направим ось y по траектории прямолинейного движения тела в сторону его движения и примем за начало координат начальное положение тела. Если начальная скорость равна нулю, то начальные условия рассматриваемого движения будут иметь вид:

Дифференциальное уравнение этого прямолинейного движения тела под действием силы тяжести примет вид:

, т.е. ускорение движения постоянно.

3. Понижаем порядок производной: .

4. Разделяем переменные:

5. Вычисляем интегралы от обоих частей уравнения:

6. Представим проекцию скорости как производную координаты по времени:

7. Разделяем переменные:

8. Вычисляем интегралы от обоих частей уравнения:

Постоянные и определим по начальным условиям. При подстановке в первое уравнение , получаем, что . При подстановке во второе уравнение , получаем, что .

Уравнения, характеризующие свободное падение тела при значениях и , примут вид:

, .

С их помощью можно определить время свободного падения тела с высоты H:

, .

П ример 2: сила зависит от времени.

Груз весом P начинает двигаться по гладкой горизонтальной поверхности под действием силы F, величина которой пропорциональна времени (F = kt) (рис.4). Определить пройденное расстояние грузом за время t.

1. Выбираем систему отсчета (декартовые координаты) так, чтобы тело имело положительную координату.

2

Рисунок 4

. Принимаем объект движения за материальную точку (тело движется поступательно), освобождаем от связи (опорной плоскости) и заменяем реакцией (нормальной реакцией гладкой поверхности).

3. Составляем основное уравнение динамики:

4. Проецируем основное уравнение динамики на ось x : или

5. Понижаем порядок производной:

6. Разделяем переменные:

7. Вычисляем интегралы от обоих частей уравнения:

8. Определим значение постоянной из начального условия , : .

9. Запишем проекцию скорости как производную координаты по времени: .

10. Разделяем переменные: .

11. Вычисляем интегралы от обоих частей уравнения:

.

12. Определим значение постоянной из начального условия

, :

В итоге получаем уравнение движения (по оси x), которое дает значение пройденного пути за время t: .

Пример 3: сила зависит от координаты. Материальная точка массой m брошена вверх с поверхности Земли со скоростью . Сила притяжения Земли обратно пропорциональна квадрату расстояния от точки до центра тяготения (центра Земли) (рис.5). Определить зависимость скорости от расстояния y до центра Земли.

1 . Выбираем систему отсчета (декартовые координаты) так, чтобы тело имело положительную координату.

2. Составляем основное уравнение динамики:

3. Проецируем основное уравнение динамики на ось y:

или .

Коэффициент пропорциональности можно найти, используя вес точки на поверхности Земли:

Рисунок 5

, тогда .

С учетом этого дифференциальное уравнение имеет вид: или .

4. Понижаем порядок производной: .

5. Делаем замену переменной: .

6. Разделяем переменные:

7. Вычисляем интегралы от обоих частей уравнения:

.

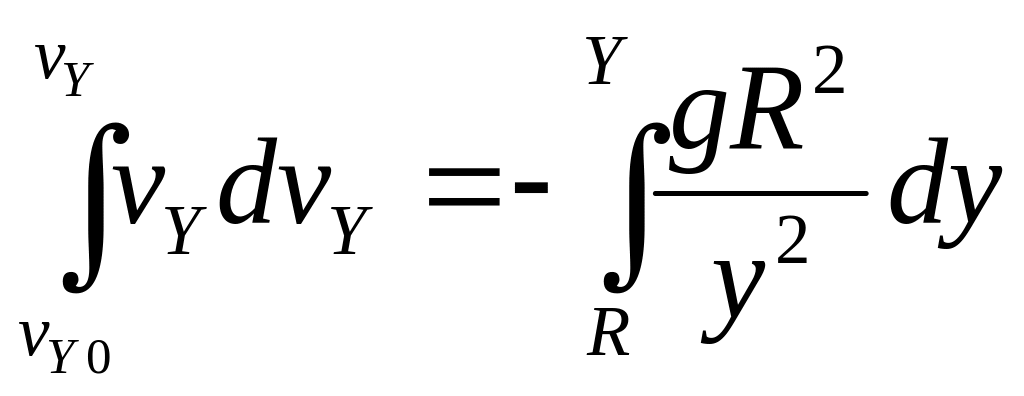
8. Подставляем пределы: .

В итоге получаем выражение для скорости как функции от координаты y : .

Максимальную высоту полета можно найти, приравнивая скорость нулю:

.

Максимальная высота полета ®¥ при обращении знаменателя в нуль: . Отсюда при постановке радиуса Земли и ускорения свободного падения получается II космическая скорость: .

П ример 4: сила зависит от скорости. Судно массы m имело скорость (рис.5). Сопротивление воды движению судна пропорционально скорости. Определить время, за которое скорость судна упадет вдвое после выключения двигателя, а также пройденное судном расстояние до полной остановки.

1 . Выбираем систему отсчета (декартовые координаты) так, чтобы тело имело положительную координату.

2

Рисунок 6

. Принимаем объект движения за материальную точку (судно движется поступательно), освобождаем от связей (воды) и заменяем реакцией (выталкивающей силой – силой Архимеда), а также силой сопротивления движению.

3. Добавляем активную силу (силу тяжести).

4. Составляем основное уравнение динамики:

5. Проецируем основное уравнение динамики на ось x : или .

6. Понижаем порядок производной: .

7. Разделяем переменные: .

8. Вычисляем интегралы от обоих частей уравнения:

.

9. Подставляем пределы интегрирования: .

Получено выражение, связывающее скорость и время t, с использованием которого можно определить время движения: . Для определения пройденного пути обратимся к выражению, полученному после понижения порядка производной, и сделаем замену переменной:

.

После интегрирования и подстановки пределов получаем: . Пройденный путь до остановки: .

Движение точки, брошенной под углом к горизонту, в однородном поле силы тяжести без учета сопротивления воздуха.

О

Рисунок 7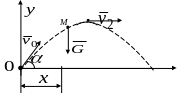

пределим движение тела М, брошенного под углом к горизонту с начальной скоростью , пренебрегая сопротивлением воздуха и принимая тело за материальную точку (рис.7).

Совместим начало координат 0 с точкой вылета тела, направив ось по горизонтали вправо, а ось - вверх по вертикали. Получим начальные условия движения:

, , , , .

Основное уравнение динамики:

Составим дифференциальные уравнения движения тела под действием постоянной силы тяжести в декартовых координатах:

.

Проекции ускорения точки из этих уравнений: , .

Полученные уравнения показывают, что проекция скорости тела на горизонтальную ось постоянна и горизонтальное перемещение тела совершается по закону равномерного движения со скоростью , т.е. по инерции. А вертикальное движение тела является равнопеременным: при подъеме оно замедленное, так как направления вертикальной составляющей скорости и ускорения силы тяжести противоположны, а при спуске - ускоренное, так как эти направления совпадают. Исключив время из уравнений движения, получаем уравнение траектории: . Траектория представляет собой параболу с вертикальной осью и вершиной в наивысшей точке. Форма траектории тела, движущегося в пустоте под действием силы тяжести, была впервые установлена Галилеем.

Время полета определяем приравниванием координаты y нулю:

Дальность полета определяем подстановкой времени полета:

.

Таким образом, дальность полета тела при одной и той же скорости вылета тела зависит от угла . Очевидно, что наибольшая дальность полета наблюдается при , т.е. при .

Наибольшую высоту подъема тела при заданной начальной скорости и при угле можно определить из условия, что в наивысшей точке проекция скорости на вертикальную ось равна нулю:

, откуда , .