
- •3 Анализ сар
- •3.2 Анализ устойчивости системы
- •3.2.1 Алгебраический критерий (критерий Гурвица)
- •3.2.2 Частотный критерий (критерий Найквиста)
- •3.2.3 Определение запаса устойчивости системы
- •3.3 Качество управления системы
- •3.3.1 Определение статической ошибки
- •3.3.2. Величина перерегулирования
- •3.3.3. Время переходного процесса
3 Анализ сар
3.1 Определение коэффициента передачи корректирующего элемента усилителя
Для определения коэффициента передачи корректирующего элемента усилителя ККЭ можно воспользоваться методикой измерения в [1].
В
качестве исходных данных здесь необходимо
использовать ограничения по статической
ошибке САР, заданные для технологического
процесса (согласно заданию) как y0
± Δy=-20![]() .
При
этом следует помнить, что по определению,
статическая ошибка равна разности между
установившимся значением контролируемого
параметра yуст
и
его заданным значением y0,
то есть
.
При
этом следует помнить, что по определению,
статическая ошибка равна разности между
установившимся значением контролируемого
параметра yуст
и
его заданным значением y0,
то есть
Δy = yуст - y0 ,
ууст=-20+1=-19,
ууст=-20-1=-21,
-21<ууст<-19.
Между передаточной и переходной характеристиками линейной системы с постоянными параметрами лежит связь, позволяющая утверждать что
К(0) = h(∞).
Значение
h(∞)
характеризует
состояние САР в установившемся режиме,
когда все переходные процессы
заканчиваются. При t
→ ∞
контролируемый пара метр
y
→ yуст.
Предположив, что р
= 0, выражение
для передаточной функции САР, после
преобразований имеет вид:
метр
y
→ yуст.
Предположив, что р
= 0, выражение
для передаточной функции САР, после
преобразований имеет вид:
![]()
где А=КУ ·КИМ ·КОР=180·0,9·0,07=11,34;
В=1+КОС ·КУ ·КИМ ·КОР=1+0,95·220·1,1·0,07=1+16,093=10,639.
Если использовать испытательный сигнал в виде y0 1(t), то получим переходную характеристику также в виде y0 h(t). Тогда
yуст = y0 К(0) = y0 h(∞).
Но согласно заданию
y0
-
Δy
≤
yуст≤
y0
+
Δy
или
y0
-
Δy
≤
![]() ≤
y0
+
Δy
.
≤
y0
+
Δy
.
В последнем неравенстве неизвестным является параметр ККЭ, значения которого несложно определить из системы:
(y0
- Δy)
(![]() )
≤ y0
А;
)
≤ y0
А;
(y0 + Δy) ( ) ≥ y0 А.
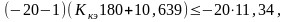
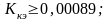
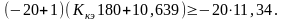
![]()
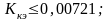
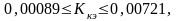
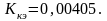
Так как в системе имеются звенья, охваченные обратной связью, то их заменяют одним эквивалентным звеном. Так для усилителя, входящего в состав САР (рисунок 1), передаточная функция будет иметь вид:
![]() ,
,
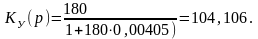
Передаточная функция САР с обратной связью определяет взаимосвязь между регулируемой величиной у(t) и задающим воздействием у0. В операторной форме эта взаимосвязь описывается передаточной функцией К(р):
![]()
где Кп(р) – передаточная функция прямой передачи системы;
Кр(р) – передаточная функция разомкнутой системы;
Кос(р)–передаточная функция цепи обратной связи.
Согласно схемы САР (рисуноук 1):
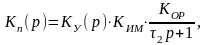
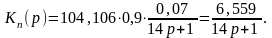
Передаточная функция разомкнутой системы:
Кр(р) =Кос(р)Кп(р);
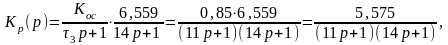
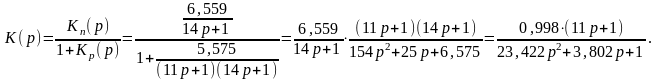
3.2 Анализ устойчивости системы
Устойчивость системы – ее способность восстанавливать состояние равновесия после прекращения внешнего воздействия.
Для определения устойчивости САР существуют критерии устойчивости.
3.2.1 Алгебраический критерий (критерий Гурвица)
Данный критерий основан на анализе коэффициентов характеристического уравнения замкнутой САР:
![]()
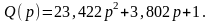
Согласно критерию Гурвица САР будет устойчива, если все коэффициенты характеристического уравнения n-го порядка положительны и все определители Гурвица до (n-1)-го порядка больше нуля.
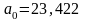 ,
,
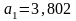 ,
,
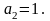
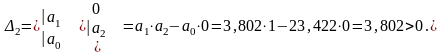
Так
как при а0>0,![]() то САР устойчива.
то САР устойчива.
