1.3. Две основные задачи динамики для материальной точки и их решение

Первая (прямая) задача.

Зная закон движения и массу точки, определить силу, действующую на точку.

Для решения этой задачи необходимо знать ускорение точки. В задачах этого типа оно может быть задано непосредственно либо задан закон движения точки, в соответствии с которым оно может быть определено.

1. Так, если движение точки задано в декартовых координатах , , , то определяются проекции ускорения на оси координат , и , а затем — проекции , и силы на эти оси:

, , . (1.5)

Модуль и направление силы определяется по формулам

, , (1.6)

2. Если точка совершает криволинейное движение и известен закон движения , траектория точки и ее радиус кривизны , то удобно пользоваться естественными осями, а проекции ускорения на эти оси определяются по известным формулам: а) на касательную ось — касательное ускорение; б) на главную нормаль 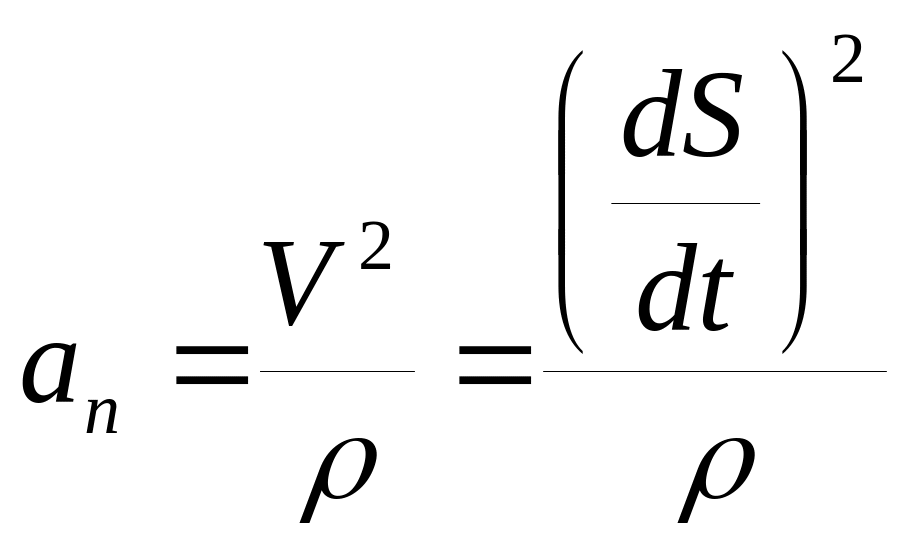— нормальное ускорение. Проекция ускорения на бинормаль равна нулю. Тогда проекции силы на естественные оси

, (1.7)

Модуль и направление силы определяется по формулам .

, . (1.8)

3. Ускорение точки может быть также определено на основании формул равнопеременного движения.

; (1.9)

где — время движения точки; — пройденное за это время расстояние; и — начальная и конечная скорости точки; — касательное ускорение.

При прямолинейном движении , , следовательно, ускорение при определяется по одной из формул

, (1.10)

Вторая (обратная) задача.

Зная действующие на точку силы, ее массу и начальные условия движения, определить закон движения точки или какие-либо другие ее кинематические характеристики.

Начальные условия движения точки в декартовых осях — это координаты точки , , и проекции начальной скорости на эти оси , и в момент времени, соответствующий началу движения точки и принимаемый равным нулю.

Решение задач этого типа сводится к составлению дифференциальных уравнений (или одного уравнения) движения материальной точки и их последующему решению путем непосредственного интегрирования или с использованием теории дифференциальных уравнений.

Тема 2. Введение в динамику механической системы

2.1. Основные понятия и определения

Механической системой или системой материальных точек называют совокупность взаимодействующих между собой материальных точек.

Примеры механических систем:

1. материальное тело, в том числе и абсолютно твердое, как совокупность взаимодействующих материальных частиц; совокупность взаимосвязанных твердых тел; совокупность планет солнечной системы и т. д.

2. Стая летящих птиц не является механической системой, т. к. между птицами нет силового взаимодействия.

Свободная механическая система — система, на движение точек которой не наложено никаких связей. Например: движение планет солнечной системы.

Несвободная механическая система — система, на движение точек которой наложены связи. Например: движение деталей в любом механизме, машине и т. п.