
Сарієнко В.К.
Розширення поняття про число
Курс лекцій
Слов’янськ
2009
УДК 51(075.32)
ББК 22.1я73 С 811
В.К. САРІЄНКО. Розширення поняття про число.
Навчальний посібник для студентів факультетів підготовки вчителів початкових класів педагогічних вищих навчальних закладів.
У посібнику викладений навчальний матеріал з теорії звичайних та десяткових дробів. Подається матеріал про відсотки та пропорції, дійсні числа. Матеріал розроблений відповідно до навчальної програми з математики для педагогічних університетів та інститутів.
Сарієнко В.К., 2009
РОЗШИРЕННЯ ПОНЯТТЯ ПРО ЧИСЛО
Як свідчить історія, натуральні числа утворилися в результаті потреби рахувати, визначати чисельність множини, а дроби утворилися в результаті вимірювання величин.
Нагадаємо, що вимірюванням називається сукупність дій, які виконуються за допомогою засобів порівняння заданого об'єкта з якимось іншим об'єктом з тієї ж множини, який ми приймаємо за одиницю виміру, з метою визначення числового значення вимірюваного об'єкта у визначених одиницях виміру. Під одиницею виміру ми розуміємо умовно вибраний об'єкт, якому у відповідність ставимо число 1. При цьому, як ми говорили, Якщо одиниця виміру "вміщується" в заданому об'єкті цілу кількість разів, то результат виміру (міра) буде виражений цілим числом. Якщо ж одиниця виміру "не вміщується" цілком в обраному об'єкті цілу кількість разів, то для вираження результату вимірювання треба розширити запас чисел, тобто ввести числа, відмінні від натуральних.
Нагадаємо, що якщо для елементів а i b з множини Р існує такий елемент m, що a = km, a b = lm, то елементи a i b називаються сумірними. Якщо ж такого елемент m не існує, то відрізки називаються несумірними. Такий елемент т називається спільною мірою елементів а і b.
Нехай у множині Р елементу е поставимо у відповідність число 1. Тоді, якщо елемент m = e, то міра елементів а і b буде виражатися цілим числом (а = kе, b = le). Якщо ж m < e, тобто в елементах a (або b) цілу кількість разів вміщується не весь одиничний елемент е, а його якась частина, то у цьому випадку постає задача розбиття одиниці виміру на менші частини, і міра даних елементів буде виражена вже не цілим числом, а числом іншого виду, так званими дробами.
В чому ж їх суть? Розглянемо це питання на прикладі вимірювання відрізків, хоча це можуть бути і елементи будь-якої іншої множини (поверхні, тіла ...).
Нехай нам задана властивість А (довжина), яку мають елементи a, b, с,... деякої множини відрізків М. Виберемо за одиницю виміру відрізок e, тобто поставимо у відповідність відрізку e число 1. Виберемо з множини М якийсь відрізок a і встановимо відповідність між цим відрізком і одиничним відрізком е, тобто встановимо міру відрізка а. Тут можливі два варіанти: відрізки a i e сумірні або несумірні.
Розглянемо варіант, коли відрізки a i e сумірні. Тоді існує такий третій відрізок х, який міститься у відрізку а т разів, а у відрізку е - п разів, тобто а = тх і е = пх. Тобто у цьому випадку відрізок х буде спільною мірою відрізків а і е. Тут можливі два випадки:
1) п = 1. Тоді е = х і а = mе, тобто одиниця виміру міститься у відрізку а цілу кількість разів, і довжина відрізку буде виражена цілим числом;
2)
n
![]() 1. Тоді х
=
1. Тоді х
=
![]() i а
=
i а
=
![]() e.
З цього ясно, що елемент
а
містить у собі п
елементів х,
кожний з яких складає
e.
З цього ясно, що елемент
а
містить у собі п
елементів х,
кожний з яких складає
![]() частину е.
Тут вимірювання характеризується двома
натуральними числами т
і п.
Число п
визначає, на скільки рівних частин
розділена одиниця виміру е,
а число т
визначає, скільки разів
частина одиниці міститься в елементі
а.
Вираз
називається звичайним
дробом.
частину е.
Тут вимірювання характеризується двома
натуральними числами т
і п.
Число п
визначає, на скільки рівних частин
розділена одиниця виміру е,
а число т
визначає, скільки разів
частина одиниці міститься в елементі
а.
Вираз
називається звичайним
дробом.
Означення. Звичайним дробом називається пара натуральних чисел т і п, записаних у вигляді , де п показує, на скільки частин розбита одиниця, а m показує, скільки таких частин в даній величині міститься.
Число т називається чисельником, а число п - знаменником.
Таким чином, оскільки одиниця виміру е не вміщується в відрізку а цілу кількість разів, то ми фактично перейшли на меншу одиницю х, яка в п разів менша за е.
Дріб, в якому чисельник менший за знаменник, зветься правильним, якщо ж навпаки, то неправильним.
Запис, що складається із цілого числа і дробу називається мішаним числом.
Довжина одного і того ж відрізка а при заданому одиничному відрізку е може бути виражена різними дробами.
Означення. Дроби, які виражають міру одного і того ж об’єкту, називаються еквівалентними (рівносильними).
Якщо
спільну міру х
розбити на к
частин, кожна з яких буде мати довжину
р,
тобто х =
кр,
то буде: е
= кnр,
а а
= кmр.
Тоді довжина того ж відрізка а
буде виражена
дробом
![]() .
Звідси випливає властивість, яка одержала
назву основної
властивості дробу.
“Якщо
чисельник і знаменник дробу помножити
(або
поділити) на
будь-яке натуральне число, то одержимо
дріб, рівносильний даному. Тобто
~
.
.
Звідси випливає властивість, яка одержала
назву основної
властивості дробу.
“Якщо
чисельник і знаменник дробу помножити
(або
поділити) на
будь-яке натуральне число, то одержимо
дріб, рівносильний даному. Тобто
~
.
Ця властивість лежить в основі такого перетворення, як скорочення дробів. В цьому разі в чисельнику і знаменнику виділяють найбільший спільний дільник і на нього ділять чисельник і знаменник.
Теорема.
Дроби
i
![]() будуть
рівносильні, якщо
тр = пк.
будуть
рівносильні, якщо
тр = пк.
Дійсно, нехай тр = пк. Поділивши обидві частини цієї рівності на добуток пр, отримаємо рівність = . Оскільки вони рівні, то відображають довжину одного і того ж відрізку, тобто можна записати ~ .
Навпаки,
якщо
~
,
то вони відображають довжину одного і
того ж відрізка. Помноживши чисельник
і знаменник першого дробу на р,
а другого на п,
отримаємо
![]() ~
~
![]() .
Оскільки ці дроби мають однакові
знаменники, то еквівалентні вирази
і
можуть виражати довжину одного і того
ж відрізку тільки в тому разі, якщо тр
= пк. Що і
треба було довести.
.
Оскільки ці дроби мають однакові
знаменники, то еквівалентні вирази
і
можуть виражати довжину одного і того
ж відрізку тільки в тому разі, якщо тр
= пк. Що і
треба було довести.
Звідси дуже легко зробити висновок, що > , якщо тр > пк і < , якщо тp < nk.
Оскільки
довжина відрізку повинна виражатися
одним додатнім числом, то еквівалентні
дроби є різними представниками одного
і того ж числа. Додатні
числа, які можна представити у вигляді
,
називаються
додатними раціональними числами.
Інакше можна сказати, що раціональним
числом називається множина еквівалентних
дробів виду
.
Таким чином, множина дробів {![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
... ;
;
... ;
![]() ;...}
є додатнім раціональним числом. Серед
цієї множини є дріб, у якого чисельник
і знаменник взаємно прості. Такий дріб
називається нескорочуваним. Він є
головним представником множини названих
еквівалентних дробів. Таким чином,
раціональні числа (як множини еквівалентних
дробів) мають властивість, що для
будь-якої
множини
еквівалентних дробів
існує
один
і
тільки один
дріб, чисельник
і
знаменник
якого
взаємно
прості.
;...}
є додатнім раціональним числом. Серед
цієї множини є дріб, у якого чисельник
і знаменник взаємно прості. Такий дріб
називається нескорочуваним. Він є
головним представником множини названих
еквівалентних дробів. Таким чином,
раціональні числа (як множини еквівалентних
дробів) мають властивість, що для
будь-якої
множини
еквівалентних дробів
існує
один
і
тільки один
дріб, чисельник
і
знаменник
якого
взаємно
прості.
В п р а в и.
1. Виберіть одиничний відрізок е і побудуйте відрізок, довжина якого складає
![]() е
;
е
;
![]() е;
е;
![]() е;
е;
![]() е.
е.
Знайдіть спільну міру відрізків довжиною 3м 42см і 60см; 21м 06см і 6м 12см ; 409см і 41мм; 4м 13см і 419см; загальну міру маси 720г і 325г; 28кг 35г і 41кг 16г; загальну міру часу; 7год і 12хв; 35хв і 1год 20хв; 2год 24хв і 36хв; 1год і 13сек; 41хв і 35сек.
Складіть множини дробів, еквівалентних дробам ; ; .
На множині дробів
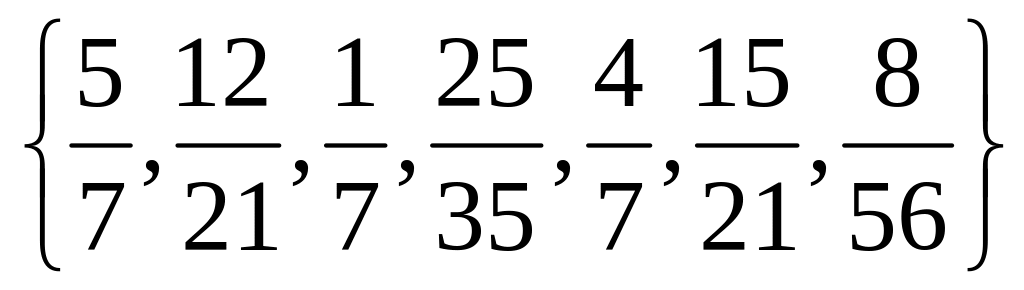 задано відношення еквівалентності.
Виберіть підмножини еквівалентних
дробів.
задано відношення еквівалентності.
Виберіть підмножини еквівалентних
дробів.
5.
Порівняйте дроби:
![]() і
і
![]() ;
;
![]() і
і
![]() ;
;
![]() і
і
![]() ;
;
![]() і
і
![]() ;
;
![]() і
і
![]() .
.
