Определение объема тела

Понятие объема в пространстве вводится аналогично понятию площади для фигур на плоскости.

О пределение 6.1. 

Тело называется простым, если его можно разбить на конечное число треугольных пирамид.

В частности, любой выпуклый многогранник является простым телом.

О пределение 6.2. 

Объемом тела называется положительная величина, характеризующая часть пространства, занимаемую телом, и обладающая следующими свойствами:

• равные тела имеют равные объемы; при параллельном переносе тела его объем не изменяется;

• если тело разбить на части, являющиеся простыми телами, то объем тела равен объему его частей;

• за единицу объема принят объем куба, ребро которого равно единице длины;

О пределение 6.3. 

Тела с равными объемами называются равновеликими. Из свойства 2 следует, что если тело с объемом V₁ содержится внутри тела с объемом V₂, то V₁ < V₂.

Т еорема 6.1. 

Объем прямоугольного параллелепипеда равен произведению его измерений: V = abc.

Т еорема 6.2. 

Объем прямой призмы равен произведению площади основания на высоту: V = SH.

Доказательство

Начало формы Конец формы Чертеж 6.1.1 Пусть ABCA1B1C1 – прямая треугольная призма, причем ее основание – прямоугольный треугольник ABC (чертеж 6.1.1). Дополним эту призму до прямоугольного параллелепипеда ACBDA1C1B1D1. Середина O диагонали AB1 этого параллелепипеда является его центром симметрии. Данная призма и призма ABDA1B1D1, которая дополняет данную призму до параллелепипеда, симметричны относительно точки O, а поэтому равновелики. Пусть V и V1 – соответственно объемы призмы ABCA1B1C1 и параллелепипеда, тогда, учитывая теорему 6.1, получим Начало формы Конец формы Чертеж 6.1.2 Рассмотрим произвольную прямую треугольную призму ABCA1B1C1 (чертеж 6.1.2). Если Δ ABC не прямоугольный, то его можно разбить на два прямоугольных треугольника ADC и BDC. Следовательно, V = V1 + V2 = SΔ ADC · H + SΔ BDC · H = SΔ ABC · H = S · H. Таким образом, теорема справедлива для произвольной прямой треугольной призмы. Если есть прямая n-угольная призма (n > 3), разобьем ее на конечное число прямых треугольных призм (чертеж 6.1.3). Начало формы Конец формы Чертеж 6.1.3 Сложив объемы этих треугольных призм, получим объем n-угольной призмы V = V1 + V2 + ... + Vn = (S1 + S2 + ... + Sn)H = S · H, где S1, S2, ..., Sn – площади оснований треугольных призм, S и H – площадь основания и высота n-угольной призмы.

Т еорема 6.3. 

Объем наклонной призмы равен площади перпендикулярного сечения на боковое ребро: V = S_пс · l.

Доказательство

Начало формы Конец формы Чертеж 6.1.4 Пусть – наклонная призма (чертеж 6.1.4), и – перпендикулярные сечения этой призмы. Призма прямая, причем . Заметим, что параллельный перенос на вектор переводит многогранник A2B2C2A1B1C1 в многогранник A3B3C3ABC. Следовательно, эти многогранники равновеликие. Пусть V – объем призмы ABCA1B1C1, V1 – объем призмы A3B3C3A2B2C2, V2 – объем многогранника A2B2C2ABC, тогда V + V2 = V1 + V2, откуда V = V1. Поскольку призма A3B3C3A2B2C2 прямая, то V1 = SΔ A3B3C3 · A2A3 = Sпс · l = V, что и требовалось доказать.

Т еорема 6.4. 

Объем наклонной призмы равен произведению площади основания на высоту: V = S · H.

Доказательство

Начало формы Конец формы Чертеж 6.1.5 Пусть A2B2C2 – перпендикулярное сечение наклонной призмы ABCA1B1C1 (чертеж 6.1.5), A1O – высота этой призмы. Пусть . Поскольку , а , то плоскости и ABC образуют тот же угол φ, что и прямые A1A и A1O. По теореме о площади ортогональной проекции SA2B2C2 = SABС cos φ. Согласно теореме 6.3 V = SA2B2C2 · A1A = SABС cos φ · A1A = SABС · A1O = S · H.

15.

Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:

• Предел a или b (или оба предела) являются бесконечными;

• Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].

Пусть определена и непрерывна на множестве от и . Тогда:

1. Если , то используется обозначение и интеграл называется несобственным интегралом Римана первого рода. В этом случае называется сходящимся.

2. Если не существует конечного 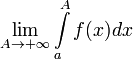( или ), то интеграл называется расходящимся к , или просто расходящимся.

Пусть определена и непрерывна на множестве от и . Тогда:

1. Если , то используется обозначение и интеграл называется несобственным интегралом Римана первого рода. В этом случае называется сходящимся.

2. Если не существует конечного ( или ), то интеграл называется расходящимся к , или просто расходящимся.

Если функция определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:

, где с — произвольное число