11. ЗАМЕНА ПЕРЕМЕННЫХ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ.ПРИМЕРЫ

. Приведем несколько примеров:

     1)

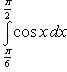
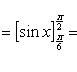
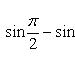
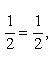
     2)

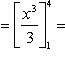
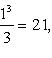
     3)

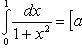
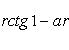
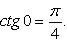
     Само собой разумеется, что все приемы, позволяющие вычислять неопределенные интегралы, применимы и тогда, когда речь идет о вычислении определенного интеграла. В частности, для вычисления определенного интеграла можно применять замену переменной и интегрирование по частям. Однако в применении к задаче вычисления определенного интеграла указанные два приема могут быть несколько специализированы.

     Теорема 1. Пусть f(z) - непрерывная функция, заданная на промежутке [p, q], а φ(x) - непрерывная функция, заданная на промежутке [a, b], имеющая там непрерывную же производную φ'(x) и удовлетворяющая неравенству p ≤ φ(x) ≤ q.

     В таком случае

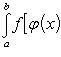
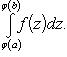     (22)

     Формула (22) выражает собой правило замены переменной в определенном интеграле. Оно напоминает правило замены переменной в интеграле неопределенном, но отличается от него тем, что здесь отпадает надобность в возвращении к старой переменной, т. к. формула (22) представляет собой равенство двух постоянных чисел. Заметим еще, что эта формула заменяет собой для случая определенных интегралов оба вида правила подстановки в интегралах неопределенных; только, применяя ее на практике, иной раз приходится читать ее слева направо, а иногда - справа налево.

     Переходя к доказательству теоремы, обозначим интегралы, входящие в левую и правую части формулы (22), соответственно через I_лев и I_прав.

     Пусть F(z) - функция первообразная для f(z). Тогда по формуле Ньютона-Лейбница/p>

I_прав = F[φ(b)] - F[φ(a)].     (23)

Что же касается I_лев, то

Но согласно теореме будет

Значит,

I_лев = F[φ(b)] - F[φ(a)].

Отсюда и из (23) следует, что I_лев = I_прав.

12.

Интегрирование по частям в определённом интеграле

   Интегрирование по частям является методом преобразования интеграла специального вида

.

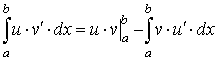   Доказательство. По правилу дифференцирования произведения имеем

.

Интегрируя обе части этого соотношения на интервале [a, b] , имеем

,

или

.

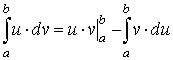Учитывая связь дифференциала с производной, окончательно получим

.

Эта формула называется формулой интегрирования по частям для определенного интеграла.

Обобщённая формула интегрирования по частям в определённом интеграле

   Многократное применение вышеприведённой формулы интегрирования по частям к интегралу вида

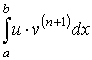
приводит к обобщённой формуле интегрирования по частям

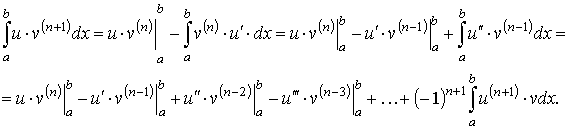
   Для облегчения выполнения интегрирования по частям рекомендуется заполнение таблицы по следующему правилу

+	—	+	…	(-1)n	(-1)n + 1
u	u '	u ''	…	u (n)	u (n + 1)
v (n)	v (n - 1)	v (n - 2)	…	v

   Умножая соответствующие элементы в столбцах этой таблицы с учётом знаков в первой строчке, получим слагаемые вне знака интеграла. Конечное интегральное слагаемое формируется с учётом соответствующего знака в первой строчке, конечного элемента второй строчки и предпоследнего элемента третей строчки таблицы.    При заполнении таблицы составляющие второй строки дифференцируется, а составляющие третьей строчки интегрируется.    Целесообразность применения формулы связаны с тем, что дифференцирование может существенно упростить один из сомножителей (при условии, что интегрирование не слишком усложнит другой).

Пример применения интегрирования по частям в определённом интеграле

   Вычислить интеграл .    Решение.

Откуда получаем рекуррентную формулу

.

Применение этой формулы приводит к интегралам

,

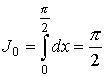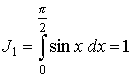
В частности

.

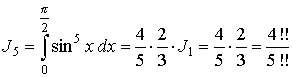13. ФОРМУЛА ТЕЙЛОРА С ОСТАТОЧНЫМ ЧЛЕНОМ В ИНТЕГРАЛЬНОЙ ФОРМЕ.

Пусть функция  имеет непрерывные производные до порядка  включительно. Тогда в силу формулы Ньютона-Лейбница

.

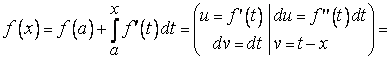
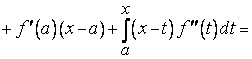
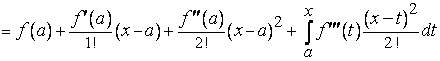Продолжая дальше процесс интегрирования по частям, получим

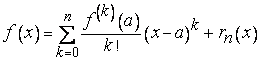,                  (1)

где

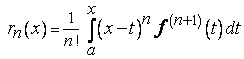.                  (2)

Формула (1), (2) называется формулой Тейлора с остатком в интегральной форме.

Применяя к интегралу (2) (по !) теорему 3 (о среднем) § 6.4, будем иметь

.

Полагая

,

получаем

,

т. е. остаточный член формулы Тейлора по степеням  в форме Коши

14

1) Давайте начнём с известной нам формулы площади круга. (слайд 6 -9) Рассмотрим окружность с центром в начале координат. Каким уравнением задаётся эта окружность? х²+у²=R²

Тогда её часть расположенная выше оси абсцисс есть график функции , где .

Используя геометрический смысл определённого интеграла площадь круга радиуса R

равна

Вычислим этот интеграл, пользуясь заменой переменной: .

При возрастании переменной ? что будет происходить с переменной х? возрастает от – R до R.

и

Тогда получим

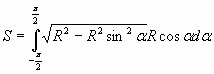
Как упростить подынтегральное выражение? Вынести R² за знак интеграла и воспользоваться основным тригонометрическим тождеством

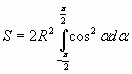
, тогда

Таким образом мы получили известную нам формулу для вычисления площади круга S=?R^2.

2)

Вычисление площадей и длин дуг кривых в декартовых координатах.

Пусть на плоскости задана область, ограниченная снизу кривой  , заданной в декартовых координатах, сверху – кривой  , слева – прямой  (ее может и не быть, если  ), справа – прямой  . Исходя из геометрического смысла определенного интеграла, площадь этой области можно вычислить по формуле 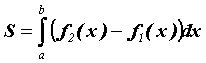 . Здесь не нужно заботиться, какая из функций и где положительная, а какая отрицательная. Если, например, , то формула сама прибавит нужную площадь. Более сложные области всегда можно разбить так, чтобы выполнялись указанные условия.

Пусть на отрезке уравнением  задана плоская кривая. Ее длина вычисляется по формуле  

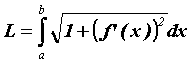
ПРИМЕР 1.  Вычисление площадей и длин дуг в декартовых координатах.

Вычисление площадей и длин дуг при параметрическом задании кривых.

Если область на плоскости снизу ограничена кривой, заданной параметрически, то есть 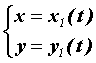 , при этом  , а сверху – кривой   . Тогда площадь такой плоской фигуры вычисляем по формуле 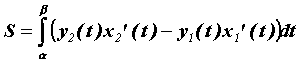. Эта формула совпадает с формулой вычисления площади в декартовых координатах, если учесть, что  .

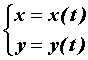
Пусть кривая на плоскости задана параметрически   . Тогда длина этой кривой вычисляется по формуле  .

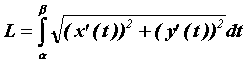3)

Кривые

на плоскости и в пространстве

Рассмотрим вектор-функцию

одного аргумента

r(t)=(x(t)y(t)z(t))=(x(t),y(t),z(t))T=x(t)i+y(t)j+z(t)k,

где i,j,k -

векторы декартова базиса. В

случае m=2 эта запись приобретает вид r(t)=x(t)i+y(t)j.

Если функции x(t),y(t),z(t) непрерывны при t∈[α,β] и начала всех векторов r(t) поместить в

начало координат, то их концы опишут в R3 некоторую кривую, называемую годографом вектор-функции r(t),

а вектор-функцию r(t) называют векторным представлением этой кривой.

Эта функция широко используется в физике

для описания движения материальной точки M, так как, чтобы знать положение

точки в момент времени t, необходимо

указать координаты этой точки как функции времени, т.е. задать ее в виде

M(x(t),y(t),z(t)).

Например, функция r(t)=acos⁡ti+asin⁡tj+btk определяет

движение точки по винтовой линии, а функция r(t)=acos⁡ti+asin⁡tj - движение точки по окружности.

Зафиксировав момент времени t=t0,

мы найдем положение точки в этот момент.

Кривую

r(t)=x(t)i+y(t)j+z(t)k назовем гладкой на [α,β], если существует r′(t) и r′(t)≠0 для всех t∈[α,β].

Непрерывную кривую назовем кусочно-гладкой на [α,β], если отрезок [α,β], можно разбить на конечное число частей, на каждом

из которых кривая гладкая.

Кривую

будем обозначать одной из букв Γ,γ,L.

Будем говорить, что кривая замкнута, если r(α)=r(β).

Если существуют значения t1,t2∈(α,β) параметра такие, что r(t1)=r(t2),

то кривая имеет самопересечения, если таких значений t1, t2 нет,

то кривая без самопересечений.

Будем

говорить, что кривая ориентирована, если задан порядок следования точек по этой

кривой при возрастании параметра от α к β. Ориентацию кривой

можно сменить, введя новый параметр, например, по формуле τ=β+α−t. Замкнутую кривую на плоскости ориентируют

обычно так, чтобы при обходе кривой против часовой стрелки область,

ограничиваемая этой кривой, оставалась слева.

Для

гладкой кривой ориентация определяется естественным образом выбором единичного

направляющего вектора касательной, так как в этом случае имеет место следующий

результат.

Теорема. В

каждой точке гладкой кривой существует касательная. Производная r′(t) направлена по этой касательной в сторону возрастания

параметра

4)