Часть 1. 1) Найти предел числовой последовательности

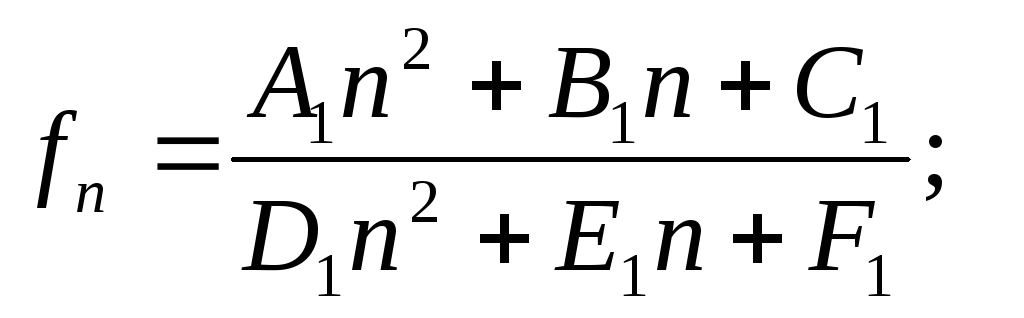
2) Записать соответствующее определение предела и доказать полученный результат: (а) по любому заданному ε найти соответствующее N_ε;.

(б) для ε=0.01, если предел конечен, и для ε=100, если предел бесконечен, указать соответствующее значение N_ε.

Часть 2. Вычислив пределы сравнить бесконечно малые функции g1,g4 и g2,g3 при

Условие задания содержит номер варианта, значения параметров и функции.

Вар	A1 B1 C1 D1 E1 F1	G1(x)	G3(x)
№	A2 B2 C2 D2 E2	G2(x)	D4(x)

Пример.

§7. Общие свойства пределов : тт. «о стабилизации знака», «предельный переход в неравенстве», «о сжатой функции».

Теорема 1("о стабилизации знака")

Если (<0), то в некоторой проколотой окрестности точкиa функция принимает лишь положительные (отрицательные) значения f(x)>0(<0) ($ d>0 "x : 0<ôx-aô<d Þ f(x)>0(<0) )

Док-во.

По определению предела

:

в частности, для e1=A/2 найдется d1 : f(x)>A-A/2=A/2>0 ч.т.д.

Теорема 2("о предельном переходе в неравенстве").

Если : (1) существуют пределы ; и (2) внекоторой проколотой окрестности точки a (ПО(а,δ)) выполняется неравенство f₁(x) £f₂(x), то пределы удовлетворяют неравенству того же смысла : A£B;

Док - во (методом "от противного").

Предположим противное : A>B Û A-B>0 Û lim(f₁(x) - f₂(x))= A - B >0; тогда по предыдущей теореме для функции φ(x)=f₁(x)-f₂(x) . Обозначимd2=min(d,d1}, тогда в ПО(а,δ2) должны выполняться два взаимоисключающих неравенства

, что невозможно, Þ сделанное предположение НЕВЕРНОЕ и A£B.

Теорема 3(о "сжатой функции").

Если 1) точка х=а является предельной для функций f₁,f₂,f; 2) и 3) в некоторой проколотой окрестности ПО(а,δ) функции удовлетворяют неравенству f₁(x)£f(x)£f₂(x), то существует предел "сжатой" функции f : .

Док - во.

По определению предела функции в точке

:

====================================================

Пример. Из курса средней школы известен предел

Рассмотрим xR :

Теорема 4. (Предел суперпозиции функций).

Если (1) существует предел и (2) функция g непрерывна в точке А (), то существует предел суперпозиции функций в точке а и он равен

Док-во.

Из определений предела и непрерывности функции в точке следует, что

(1) ==>

Замечание. Доказанная теорема полезна при "раскрытии неопределенности" вида "1^∞":

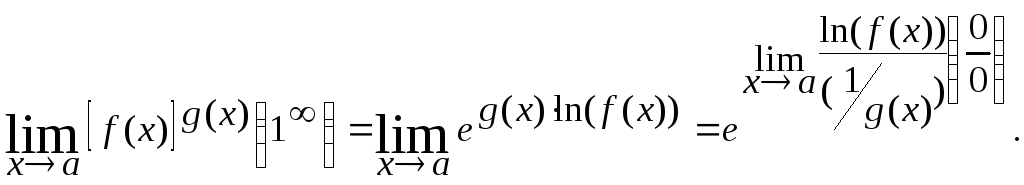
§8.Замечяательные пределы: §9. Бесконечно-малые и их сравнение; символы о(х)и о(х).

Пусть a - предельная точка области определения функции

:ПО(a;)R;(x).

Определение 1. Функция  называется бесконечно малой при x®a, если

Например, f(x)=x² - б.м. при х-->0; g(x)=ln(x) - б.м. при х-->1; h(x)=1/x - б.м. при х-->∞.

Пусть , - б/м при хa. Рассмотрим предел их отношения

Определение 2.

В зависимости от предела q бесконечно малые при x®a функции , называют :

(1) равносильными(эквивалентными) б.малыми и пишут ,если q=1.

Например,

(2)бесконечно малыми одного порядка малости и пишут (-"о большое" относительно  при xa), если q=rR/{0}.

Например, 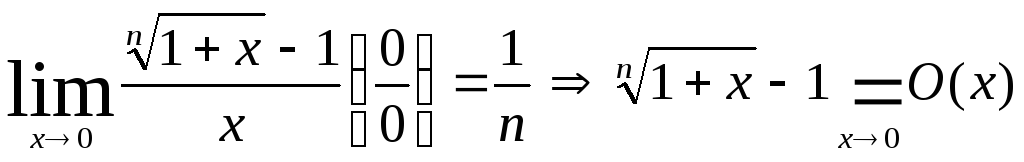(3) функцию “” называют бесконечно малой более высокого порядка малости чем “”,если q=0 и пишут (-"о малое" относительно  при xa)

Например,

Следствия.

1) Линейная комбинация бесконечно малых - бесконечно малая при x ®a f, g - б.малые Þ a(x) = С₁f(x) +C₂g(x) - б. малая;

2) Например,;

3) Произведение б. малых - б.малая более высокого порядка малости, чем любой множитель : , - б. малые при x ®a Þ (x)´(x) =o((x)).