§4.Расширенное множество вещественных чисел; числовая последовательность и ее предел.

Определение 1. Расширенным множеством вещественных чисел называют объединение множестваR со множеством из двух "несобственных элементов

"+¥” “- ¥”(плюс- и минус-бесконечность) :

Внимание!!:во множестве НЕ ОПРЕДЕЛЕНЫ операции :

1) деления: ; 2)умножения: : 3)вычетания:

Определение 2. Функция f: NC; f(n)=f_n, определенная на множестве натуральных чисел, называется числовой последовательностью; значение f(n)=f_n называют “n”-ым членом последовательности.

Например, a:NR(C);a_n=a₁+d(n-1)- арифметическая прогрессия с первым членом a₁ и разностью d; S_n=a₁+ a_2+…+ a_n=(a₁+ a_n)n/2 – сумма первых “n” членов а.п.

b: NR(C);b_n=b₁q^n-1;q0 - геометрическая прогрессия с первым членом b₁ и знаменателем q; S_n=b₁+ b₂+..+ b_n=- сумма первых “n” членов г.п.

Поскольку множество N={1,2,…} в R не имеет предельных точек, введем

Определение 3. Окрестностью и проколотой окрестностью радиуса r>0 «точек»  в называется множествовещественных чисел O(r,+)={xR;x>r); O(r,-)={xR;x<-r);

O(r,-) O(r,+)

Из этого определения следует, что во множестве множество натуральных чисел N имеет единственную предельную точку -"+¥”, а множество целых чисел Z – две предельные точки - "+¥” и "-¥”.

Следовательно, числовая последовательность a_n может иметь предел только при n. Запишем это определение:

«Для любого положительногго числа >0 найдется такой номер N_, начиная с которого все члены последовательности отличаются от А по модулю меньше чем на .»

Задание ТР: доказать, что

Док-во. (1) Зададим произвольное положительное число (0.01) и решим неравенство:

(2) Т.О. 

Например, =0.01N=1+[n=20>18

=>f₂₀=(220²+1)/(1-20²)-2.00752=>|f₂₀+2|0.008<=0.01

§5. Предел на бесконечности и бесконечный предел;

В дальнейшем будем рассматривать вещественные функции одной вещественной переменной: f:X={xR}RR; f(x).

Определения окрестности и проколотой окрестности «точки» в R и в :

O(a;r)={xR|x-a|<r}=(a-r;a+r); ПО(a;r)= O(a;r)/{a}=(a-r;a)(a;a+r)

O(-;r)ПО(-;r)={xRx<-r}; O(+;r)ПО(+;r)={xRx>r}

и общее "ε-δ" определение предела

позволяет «расшифровать» определения «бесконечного предела» функции в «точке» и предела функции «на бесконечности»:

1,2) 3,4) 5,6,7,8)

Например,

f(o.1)105; f(0.01)10050. f(0.001)10⁶ x0f(x)+

§6. Арифметические свойства пределов.

Из определения предела функции в точке следуют «свойства пределов», по степени «сложности» доказательства которых их называют «следствием», «леммой» или «теоремой».

[1]. « Предел функции-константы f:XRR; f(x)=cR равен константе С».

Доказательство этого свойства очевидно, так как >0xX |f(x)-C|=0<.

[2]. Лемма. «Если и сR, то ».

Док-во. Зададим произвольное >0 и обозначим 1=/|с|>0

ч.т.д.

!!! Постоянный множитель «выносится» за знак предела !!!

Пусть точка «а» - предельная точка для D_f и D_g.

[3]. Теорема (арифметические свойства пределов).

«Если (1) существуют пределы и (2)определены соответствующие операции (A+B; AB; A/B), то:

Докажем, например, свойство 2. Зададим произвольное число ε>0 и обозначим ε1=ε2=ε/2.

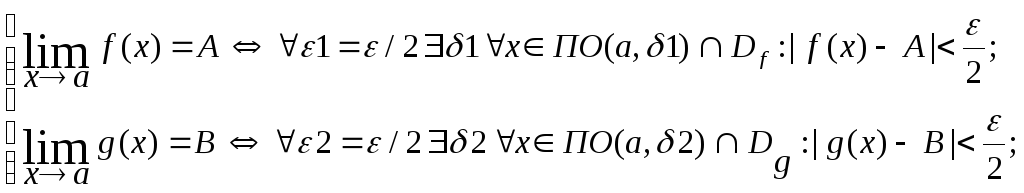
Обозначим δ=наим{δ1,δ2}. Очевидно, что для выполняются оба последних неравенства. Учитываясвойство модулей |C+D||C|+|D| и эти неравенства, запишем:

--------------------------------------------------------------------

Важное замечание. Если условия (2) теоремы не выполнены, теорема "не работает"! Так как во множестве не определены операции ,для "раскрытия этих неопределенностей" при вычислении пределов необходимо предварительно выполнить "подходящие" алгебраические преобразования функции.

--------------------------------------------------------------------

===================================

ТР по теме "Предел функции в точке; сравнение бесконечно малых".

ЗАДАНИЕ.