24

V. Введение в анализ. 2

§1. Понятие функции; суперпозиция функций; обратная функция. 2

§2. Окрестность точки. Предельная точка множества. 5

§3. Предел и непрерывность функции в точке. 6

§4.Расширенное множество вещественных чисел; числовая последовательность и ее предел. 8

§5. Предел на бесконечности и бесконечный предел; 10

§6. Арифметические свойства пределов. 11

§7. Общие свойства пределов : тт. «о стабилизации знака», «предельный переход в неравенстве», «о сжатой функции». 14

§8.Замечяательные пределы: 17

§9. Бесконечно-малые и их сравнение; символы о(х)и О(х). 17

§10.Равносильные бесконечно-малые.Таблица «равносильностей». 18

§11.Односторонние пределы и непрерывность функции в точке 20

§12.Точки разрыва функции и их классификация; вертикальная асимптота графика функции. 22

V. Введение в анализ.

§1. Понятие функции; суперпозиция функций; обратная функция.

Определение 1.

Пусть заданы: (1) множество X=D_f={x}, (2) множество Y={y} и (3) однозначное соответствие f -правило, по которому каждому элементу ставится в соответствиеединственный элемент Тогда говорят, что "на множествеX=D_f задана функция f, значения f(x) которой принадлежат множеству Y" и пишут

,

при этом

• D_f называют областью определения функции f;

• f(x) – значением функции f в точке «х»; например, f(x)=e^2xf(2)=e⁴.

• E_f={f(x); xD_f}Y- множеством значений функции f; например, E_exp(x)=(0;+)R.

Способы задания функции (однозначного соответствия !!) могут быть различными : аналитический (формула f(x)=sin(2x)), табличный , графический{x,y=f(x)}, программа-функция и т.п.

Например, на множестве квадратных матриц задана (определена) функция

А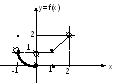налитически функция может быть задана несколькими формулами

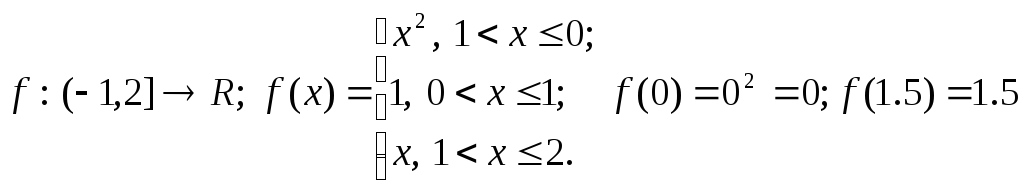
Если f(x)C (R), f называют числовой функцией.

Некоторые типы числовых функций:

Функцияназываетсяфункцией-константой; ее график - горизонтальная прямая на плоскости.

3]. f: CC; f(z) – (комплексная) функция комплексной переменной.

X

5]. F: RⁿR; f(x)=f(x₁,x₂,…,x_n) – (вещественная) функция «n» пересенных.

F: R³R; F(x,y,z)=x²+2xy+z; F(1,2,3)=1²+212+3=7

Определение 2. Пусть заданы две функции 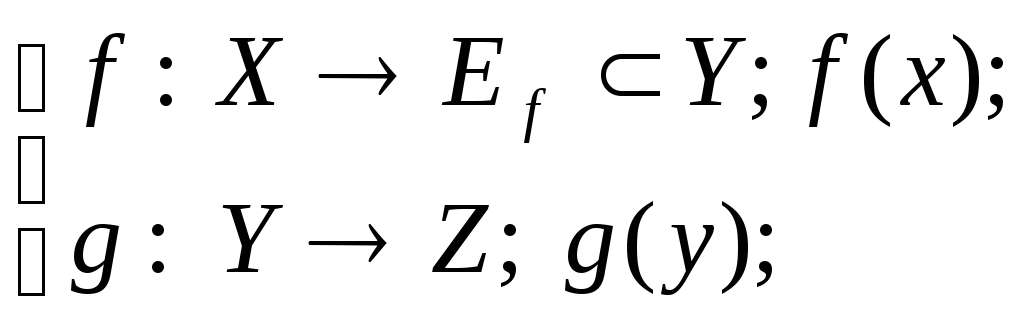, причем функцияg определена на множестве значений функции f . Из определения функции следует. ==>т.е. на множестве Х определена функция , которую называют суперпозицией функций f и g и пишут .

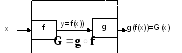
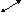
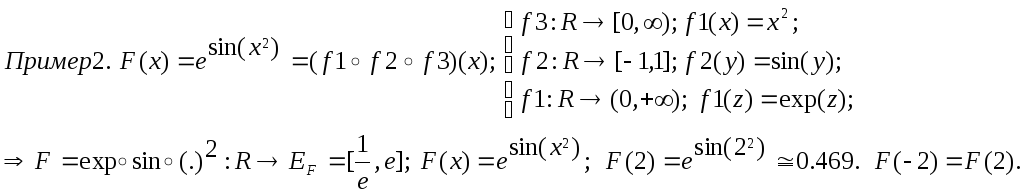
x

О

x

пределение 3.Пусть задана функция ,значения которой в разных точках области определения x₁#x₂X различны 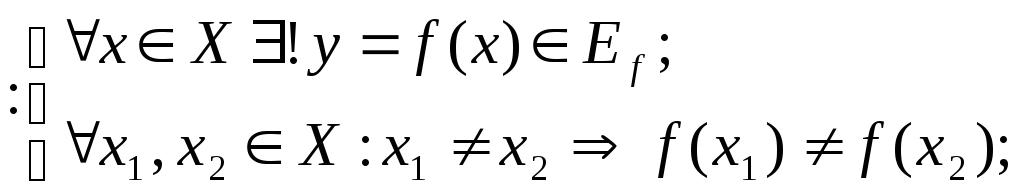Тогда, очевидно, , т.е. определена функцияf^-1: E_f которая называется обратной к функции f.

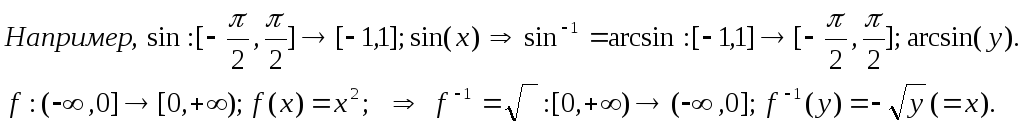
Замечание.График функции y=f(x), имеющей обратную функцию, пересекается горизонтальной прямой y=const только в одной точке. Поэтому, например, функция f(x)=x² на множестве R не имеет обратной. Однако, для функций f1: (-,0]==>R; f1(x)=x² и f2: [0,+)==>R; f2(x)=x² обратные существуют :

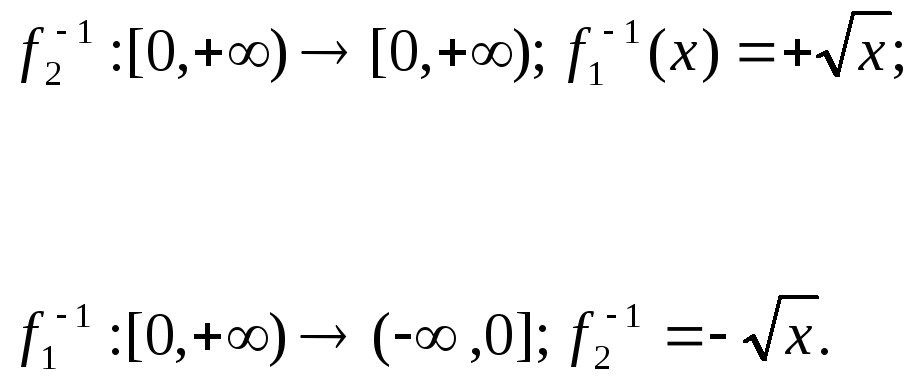
§2. Окрестность точки. Предельная точка множества.

Введем некоторые «жаргонные» понятия:

1. «ТОЧКА»: М(x1,x2,..,xn)  xRⁿ  xXRⁿ

в "n"-мерном координатном пространстве радиус-вектор элемент числового множества

«расстояние между точками» a и x  ||x-a||.

(2)- Окрестность радиуса "r0" точки а - множество точек, удаленных от точки а меньше, чем на r>0.

в R³ O(a,r) - внутренние точки шара радиуса "r" с центром в точке а;

в R² O(a,r) - внутренние точки круга радиуса "r" с центром в точке а;

в R O(а,r) - внутренние точки открытого интервала (а-r, a+r);

O(а,r)= O_ЛЕВ(а,r) O_ПРАВ(а,r)= (а-r, a] [а, a+r).

(3) ПО(a,r)= O(a,r)\ {a} - Проколотая окрестность точки.

Например,

(4) a_П.Т - предельная точка множества X={x}Rⁿ, если любая ее проколотая окрестность (любого радиуса!!) содержит точки множества, т.е.

----------------------------------------------------------------- Например,

• Предельные точки промежутка <a;b> образуют закрытый интервал [a;b], причем для открытого интервала п.т. х=а и х=в множеству не принадлежат.

Обратите внимание: 1)Предельная точка является «точкой сгущения» элементов множества.

2) Множество X={x}вопрос «зрелости»: Сколько точек множества содиржится в ПО(a,1)?=>доказать методом « от противного».

§3. Предел и непрерывность функции в точке.

Пусть для числовой функции точка x=a - предельная точка области определения (значения f(x) могут быть вычислены в сколь угодно близких к а точках, в то время как в точке «а» функция может быть и не определена !!).

Определение 1. Число называетсяпределом функции f в точке "а",

если для любого заданного радиуса r=ε>0 окрестности O(A,ε) найдется такой радиус r=δ_ε>0 проколотой окрестности точки а ПО(а,δ), значения функции f(x) в любой точке x пересечения которой с собластью определения функции - D_f=X принадлежат O(A,ε)

[если ее значения f(x) во всех точках x, достаточно близких к точке a (r=δ_ε:xПО(а,_)D_f), сколь угодно мало (>0) отличаются от числа А по модулю |f(x)-A|<].

«Важные замечания»: 1)Предел функции определен лишь в предельной точке области ее определения – функция должна быть определена в точках, сколь угодно «близких» к этой точке.

2)Определение предела позволяет

• «угадать» (предположить) предел как число, к которому «сгущаются» значения функции при xa, и

• проверить (доказать)верность этого предположения.

---------------------------------------------------------------------------

Например, "сгущаются" к 3:

X	1.1	0.95	0.99	1.001
f(x) |f(x)-3|	3.2 0.3	2.9 0.1	2.98 0.02	3.002 0.002

, поэтому естественно предположить, что .

Докажем,

• Зададим произвольное положительное число >0 и решим неравенство:

|f(x)-A|< |2x+1-3|< |x-1|</2 обозначим =/2

(2)Таким образом, >0 =/2: x: |x-1|<=/2|(2x+1)–3|< ч.т.д. 

Например, =0.1=0.05x=1.04 x-1=0.04<0.05f(1.04)-3=3.08-3=0.08<=0.1

---------------------------------------------------------------------------

Метод вычисления предела функции в точке дают следующее определение и теорема.

Определение 2. Функция f:XRR; f(x) называется непрерывной в точке «а», если предел функции в точке равен ее значению в точке:

f непр. в a  .f(x)=2x+1 – непрерывна в точке х=1.

Теорема (без док-ва). Элементарные функции и их суперпозиции непрерывны во внутренних точках области определения.

«воспоминания» об элементарных функциях:

P_n: RR; P_n(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀; exp_a: R(0;+); a^x; a>0;

Sin: R[-1;+1]; sin(x); cos: R-1;+1]; cos(x);

tg: RR; tg(x); ctg: RR; ctg(x);

arcsin: [-1;1][-/2; /2]; arcsin(x); arccos: [-1;1][0; ];arccos(x);

arctg: (-/2; /2)R;arctg(x); arcctg: (0; )R;arcctg(x);

----------------------------------------------------------------------Например, НО!!:- вычислить этот предел «по непрерывности» нельзя, так как; «угадать» его можнопо определению:

0.1	0.05	0.01	0.001	0
1.0517	1.0254	1.00502	1.000500	1.0000