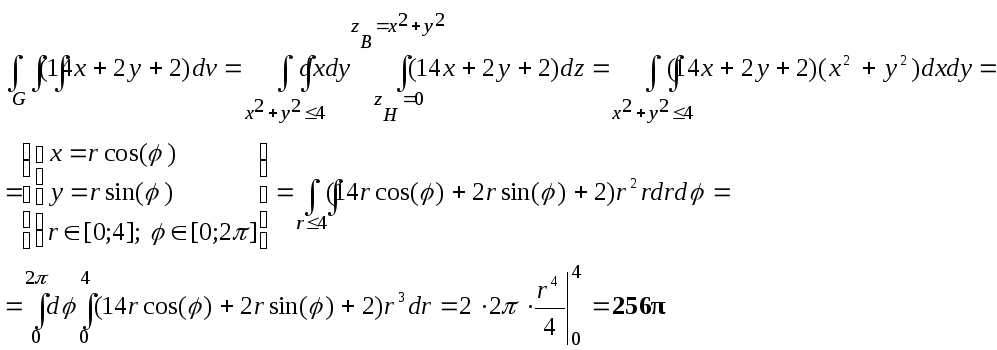§ 4.Поток вектора через поверхность.

Пусть

G€R³ - гладкая замкнутая поверхность, n– вектор ее внешней нормали в точке M € G ,

S_xy, S_xz, S_zy - проекции G на координатные плоскости и F(r)=[f_x(r); f_x(r); f_x(r)]^t – непрерывное векторное поле.

Проекция вектора F(r) на вектор n(r) в точке M(r) € G равна

,

где: e_N=[cos();cos();cos()]^t – единичный вектор внешней нормали, а ,,- углы между вектором нормали в точке и ортами соответствующих координатных осей прямоугольной системы координат, причем cos²()+cos²()+cos²()=1.

Замечаня.

1) Если поверхность задана уравнением G(x,y,z)=0, из него можно получить явный вид уравнений поверхности:(1) x=g_х(y,z), (2) y=g_у(x,z), (3) z=g_z(x,y), причем соответствующие функции g двух переменных определены и дифференцируемы в областях S_xy, S_xz, S_zy.

Например,G:x²+y²+z²=1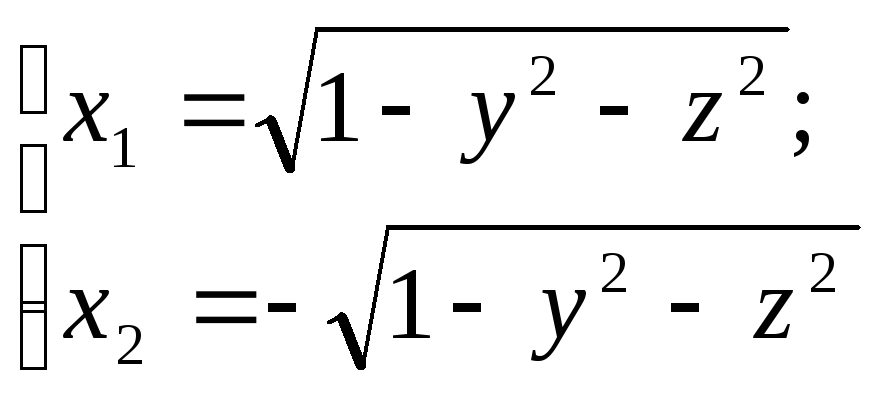-уравнения передней и задней полусфер.

2) Если в окрестности точки М€ G выделить бесконечно малую ячейку поверхности dσ, ее проекции на координатные плоскости будут равны, соответственно:

dσ_XOY=dS_xy=dσ∙|cos()|; dσ_XOZ= dS_xz= dσ∙|cos()|; dσ_YOZ= dS_zy=dσ∙|cos()|

Определение.

Потоком непрерывного вектора F(r) через кусочно-гладкую поверхность G называется двойной интеграл по поверхности от проекции векторного поля на вектор внешней нормали n к поверхности :

[1]

Следствия.

1. Из определения следуют свойства аддитивности и линейности потока вектора через поверхность: P(c₁F₁+ c₂F₂)= c₁P₁₊ c₂P₂; P(G=G₁ỤG₂)=P(G₁)+P(G₂).

2. Так как произведение элемента поверхности dσ на направляющий косинус вектора нормали с точностью до «знака» равно его проекции на соответствующую координатную плоскость dσ∙cos()=(±)dS_xy; dσ∙cos()=(±)dS_xz; dσ∙cos()=(±)dS_zy, (знак “+” соответствует острому, а “-“ тупому углу) , в общем случае вычисление потока вектора через поверхность сводится к вычислению трех двойных интегралов по проекциям поверхности на координатные плоскости:

[2]

3. Так как замкнутая поверхность проецируется на каждую координатную плоскость дважды (спереди-сзади, снизу-сверху, справа-слева) с разными по знаку направляющими косинусами, при вычислении потока вектора через замкнутую поверхность каждое слагаемое в [2] представляет разность двойных интегралов:

1. 

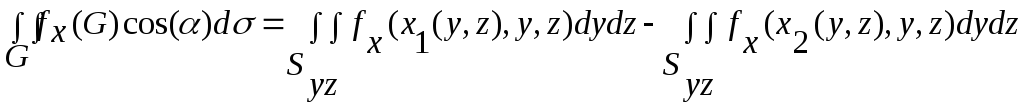
2. [3]

3.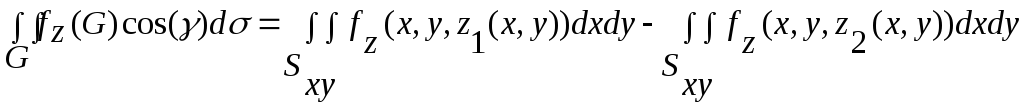 

Замечание. Объем вычислений значительно уменьшается, если поверхность G и проекции векторного поля обладают свойствами симметрии.

Например, если G является поверхностью вращения относительно координатной оси (например OZ), явные уравнения ее «противоположных» частей различаются лишь знаком (например, x₁(y,z)= -x₂(y,z); y₁(x,z)= -y₂(x,z)). Если при этом подынтегральная функция в (1),(2) является четной относительно соответствующей координаты ( f_x(-x,y,z)= f_x(x,y,z); f_y(x,-y,z)= f_y(x,y,z) ), соответствующий интеграл в [3] (слагаемое в [2]) равен нулю.

-----------------------------------------------------------------------------------------------------------------------------------

Пример.

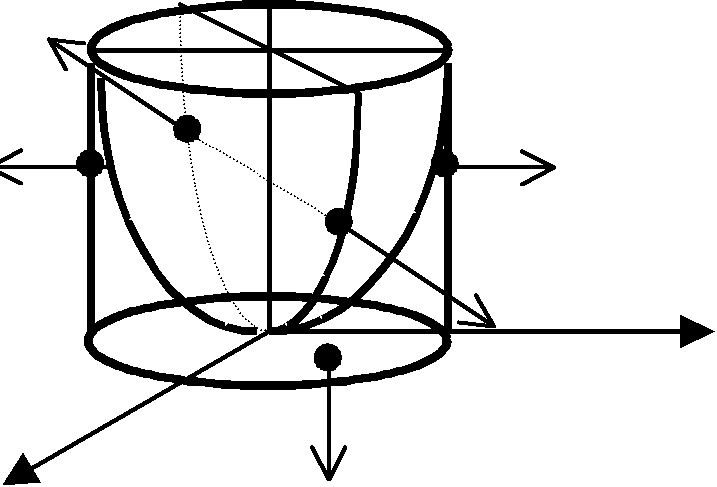
Поток Р векторного поля через замкнутую кусочно-гладкую поверхностьG= G₁ỤG₂ỤG₃, состоящую из цилиндрической поверхности G₁: x²+y² = 16, параболической поверхности вращения G₂: z=x²+y² и плоскости G₃: z=0, равен сумме потоков P=P₁ + P₂ + P₃ через каждую поверхность в направлении их внешних нормалей:

.

1. Для цилиндрической поверхности G₁

• вектор n₁ перпендикулярен OZ cos()=0,

• x_1,2(y,z)=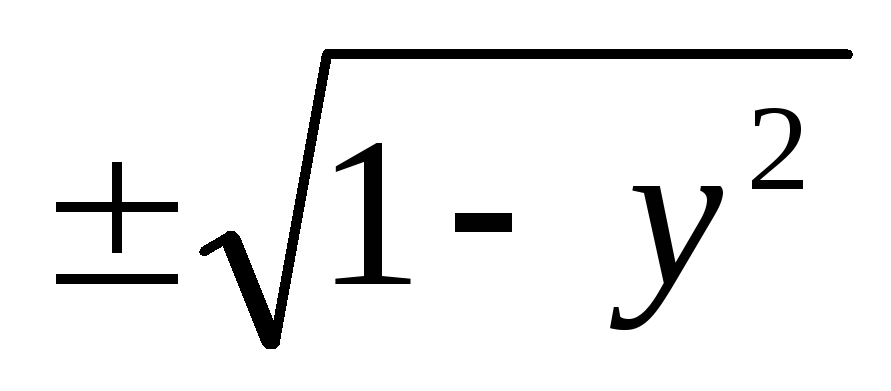; y_1,2(x,z)= 

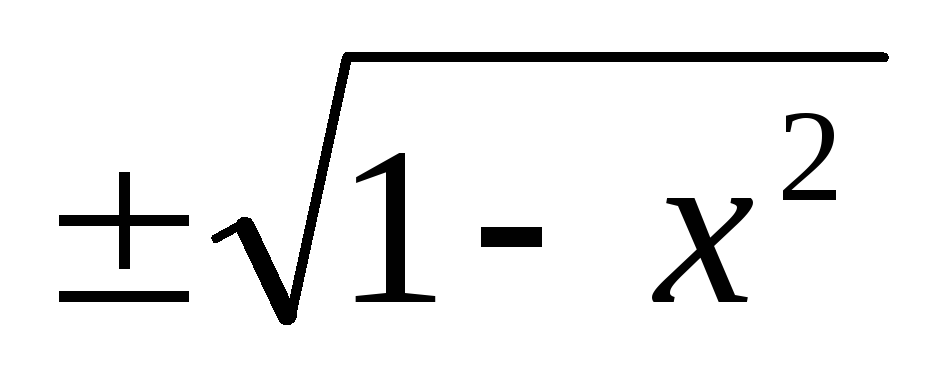
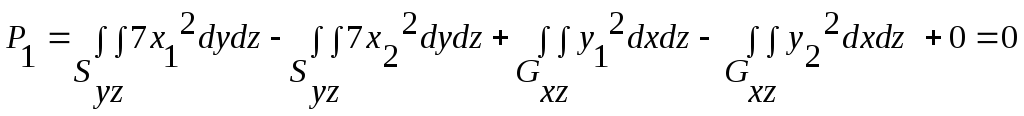
2. Для параболической поверхности G₂ x_1,2(y,z)=; y_1,2(x,z)= ,

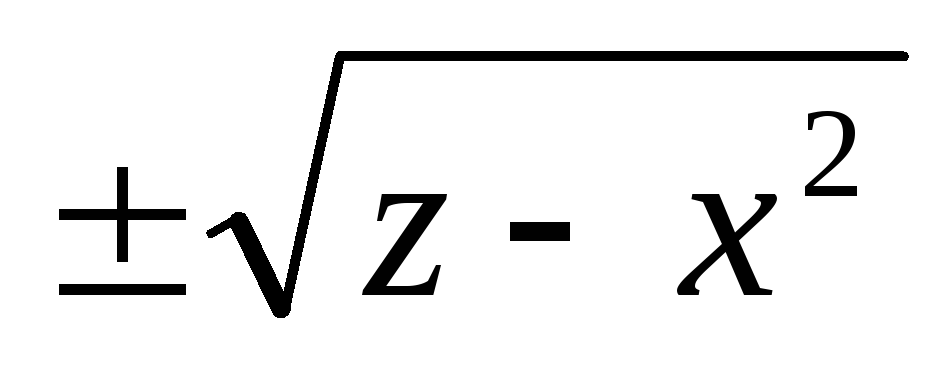f_x(-x,y,z)= f_x(x,y,z)=7x² ; f_y(x,-y,z)= f_y(x,y,z)=y² , поэтому первые два слагаемых в [2] равны нулю (так как интегралы (1)=(2)=0 в [3]), и поток Р₂ определяется третьим слагаемым:

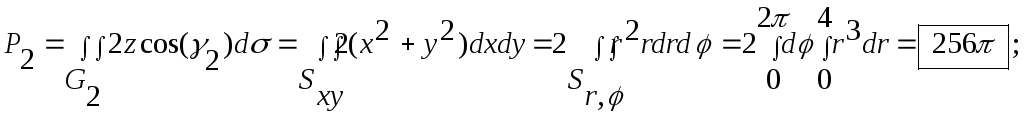
3) Поток P₃ вектора через плоскость G₃ равен нулю, так как :

• вектор нормали 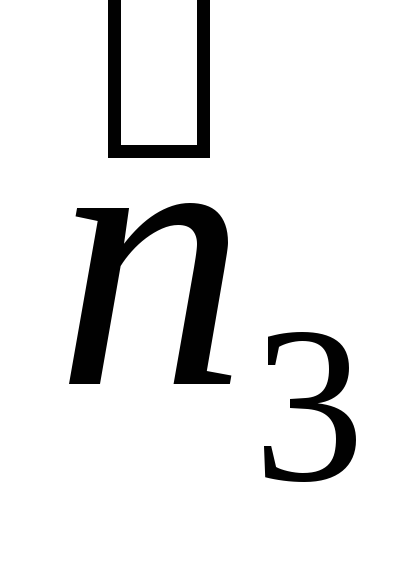||OZ  cos(α)=cos(β)=0;

• cos(γ)=-1, но z (G₃)≡0

Таким образом, поток Р векторного поля через замкнутую кусочно-гладкую поверхностьG= G₁ỤG₂ỤG₃ равен P=P₁+ P₂+ P₃ =0+256π+0=256π.

Замечание.

Для векторного поля F(r)€R³, непрерывно дифференцируемого в R³ , имеет место

Теорема Гаусса-Остроградского.

«Поток векторного поля F(r) через замкнутую поверхность G в направлении ее внешней нормали равен тройному интегралу по области D_G, ограниченной этой поверхностью:

Для рассмотренного примера: