10

§1 Векторное поле и криволинейный интеграл, его свойства и вычисление. 1

§2 Криволинейный интеграл по замкнутому контуру; формула Грина. 3

§3 Независимость к.и. от пути; потенциальное векторное поле и его потенциал. 5

§ 4.Поток вектора через поверхность. 7

§1 Векторное поле и криволинейный интеграл, его свойства и вычисление.

Пусть в области DÌR³ заданы : 1) непрерывное векторное поле

F(r) =[ f_x(x,y.z); f_y(r); f_z(r)]^t Î R³;

(координаты вектора F - непрерывные функции f_x,y,z(x,y,z) трех переменных)

и 2) параметрическое уравнение гладкой линии L Ì D, соединяющей точки A и В:

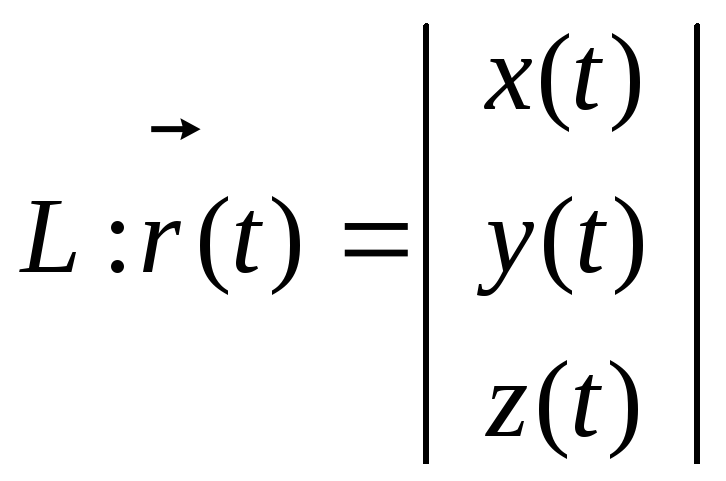; А(x(t_A), y(t_A),z(t_A))=A(t_A), B(t_B).

( функции x(t), y(t), z(t) - дифференцируемые)

Запишем в произвольной точке линии M(r(t))ÎL

-векторное поле F(t)=F(r(t))= F(x(t), y(t), z(t))=.

- и вектор dr(t) бесконечно-малого перемещения в точке (по касательной к линии L)

dr(t)=[dx(t),dy(t), dz(t)]^t

dr(t))

^{Очевидно, что скалярное произведение F(t)·dr(t) равно}

^{и определяется одной переменной - параметром “t” точки линии.}

Определение. Криволинейным интегралом (II рода по координатам) от непрерывного векторного поля F(r) вдоль гладкой кривой L : называют число

Из определения следует:

1) Так как скалярное произведение векторов ^{F(t)·dr(t)= ||F|| ||dr||cos(F,r),} для силового поля F криволинейный интеграл равен работе по перемещению материальной точки из точки А в точку В по линии L в поле силы F.

2)Алгоритм вычисления криволинейного интеграла :

а) записывается параметрическое уравнение ггладкой линии L

L : r(t) Û x=x(t); y=y(t); z=z(t);

и находятся соответствующие параметрические координаты t_А и t_В точек А и В ;

б) уравнение линии дифференцируется dr(t)=r^'(t)dt=[dx(t);dy(t);dz(t)];

в) записывается векторное поле в точках линии F(t)=[f_X^*(t); f_Y^*(t); f_Z^*(t)] ^t;

4) вычисляется скалярное произведение векторов (F(t),dr(t)) и находится явный вид подынтегрального выражения

(f_X^*(t)x’(t)+ f_Y^*(t)y’(t)+ f_Z^*(t)z’(t))dt = Ф(t)dt;

5) вычисляется определенный интеграл

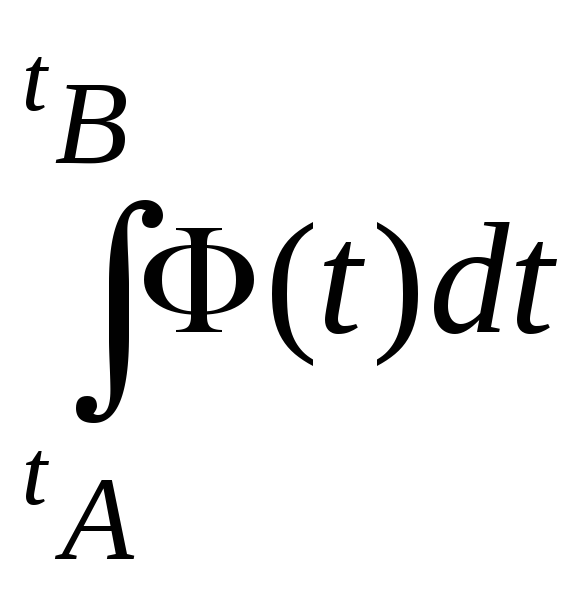
Свойства криволинейного интеграла следуют непосредственно из его определения и свойств определенного интеграла:

1) Линейность :

2) Аддитивность :

3) В общем случае, К.И. зависит от формы пути L :

4)

Пример. Вычислить

0] Восстановим векторное поле по виду подынтегрального выражения :

F(x,y,z)=[ x²y;-2y;(z+3)]^t;

1] Запишем интеграл как сумму интегралов по гладким линиям: ;

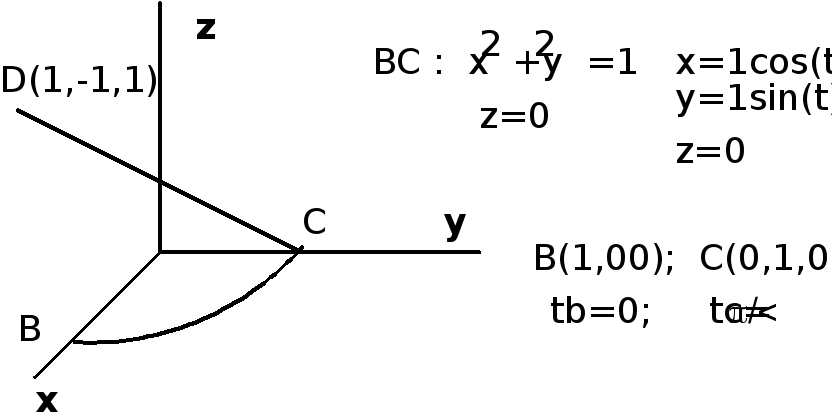
2] Запишем параметрическое уравнение линии BC - окружности радиуса 1 в цилиндри-ческих координатах: x()=1cos();y=1sin(); z=0; [0;/2]; _B=0; _C=/2 и

найдем соответствующие дифференциалы: dx()= -sin()d; dy=cos()d; dz=0.

3] Вычислим векторное поле в точках линии: F()=[sin()cos²(); -2sin(); 3]^t.

4] Вычислим криволинейный интеграл по линии ВС :

Аналогично вычисляется криволинейный интеграл по отрезку прямой СD :

; t_С =0; t_D =1; F(t)=[t²(1-2t); -2(1-2t); t+3]^t;

 F(t)dr(t)=[t²(1-2t)+4(1-2t)+(t+3)]dt  J_CD=

Таким образом, = 13/3 - /16

==============================================================