§2 Криволинейный интеграл по замкнутому контуру; формула Грина.

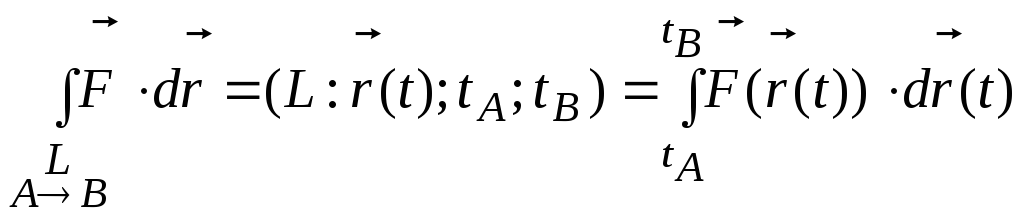
Рассмотримплоское векторное поле F, дифференцируемое в замкнутой области D_K , включающей границу – замкнутый контур «К», при положительном обходе которого (+К) внутренние точки области остаются слева от границы.

F(x,y)=[f_x(x,y); f_y(x,y)]^tR²_; Df_x,y=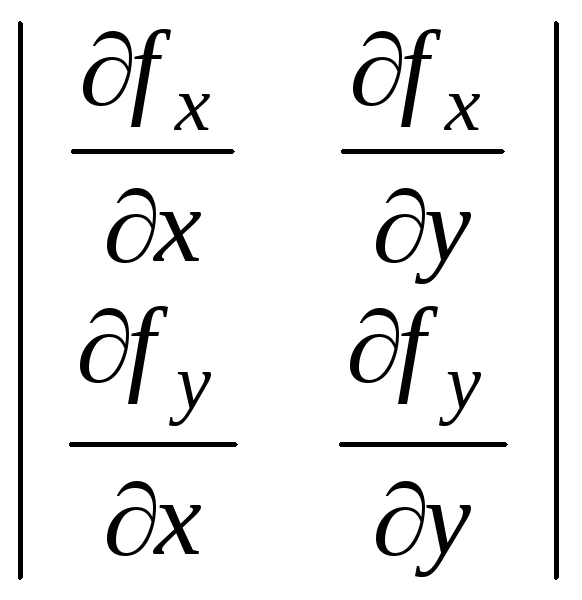 непрерывна.

Сравним два числа – криволинейный интеграл по замкнутому контуру и двойной интеграл по областиD_K

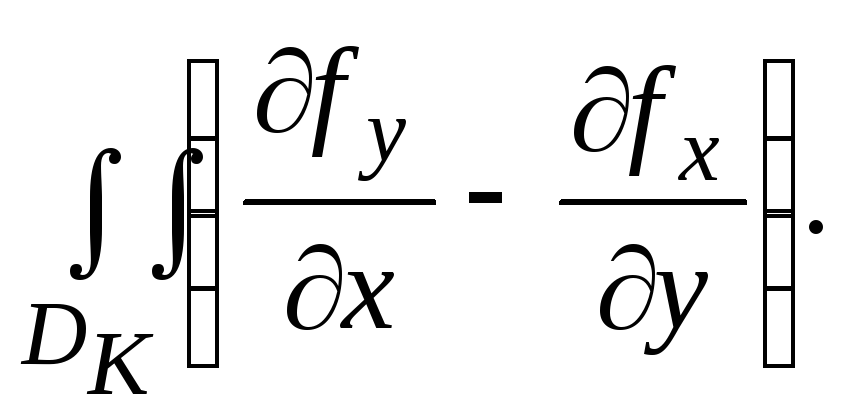
Имеет место следующая

Теорема Грина. Если плоское векторное поле F(x,y)=[f_X(x,y);f_Y(x,y)]^t непрерывно дифференцируемо в замкнутой области D_К ÌR², ограниченной гладким контуром «К», криволинейный интеграл по замкнутому контуру в положительном направлении (+К) равен двойному интегралу по области, ограниченной этим контуром

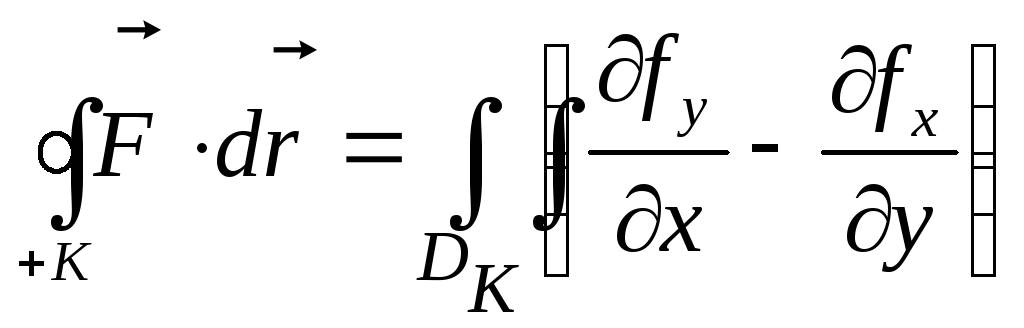- формула Грина

Доказательство. Вычислим, учитывая определение частной производной, последовательно два двойных интеграла.

1) Обозначим уравнения линий контура, ограничивающих область снизу (K_H: y_H(x)) и сверху (K_B: y_B(x)) вдоль лини x=const, и запишем двойной интеграл, выбрав соответствующий порядок интегрирования:

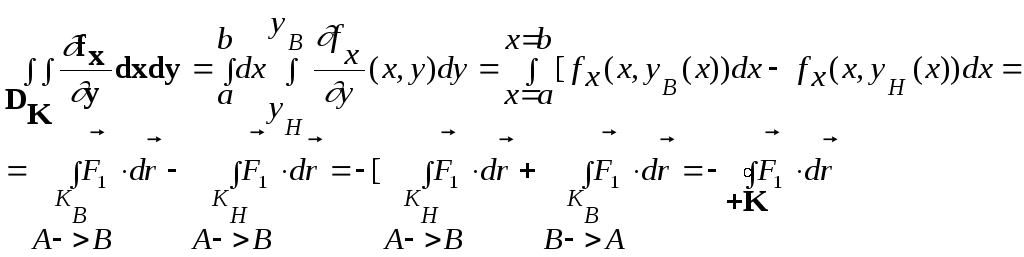F₁=[f_x;0]^t

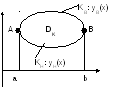
Аналогично доказывается (выполните самостоятельно), что

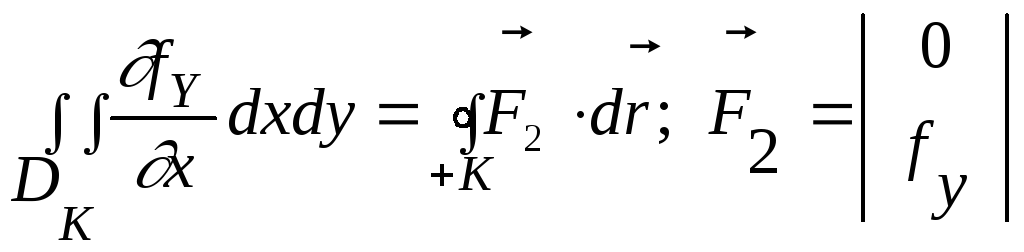
Таким образом,

--------------------------------------------------------------------------------------------------------------------------------

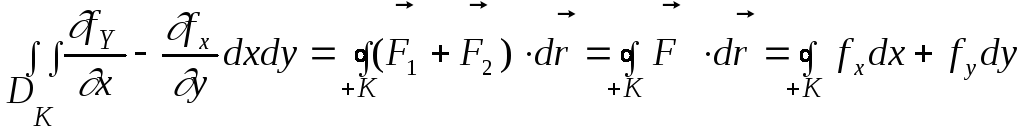
Например,

1)

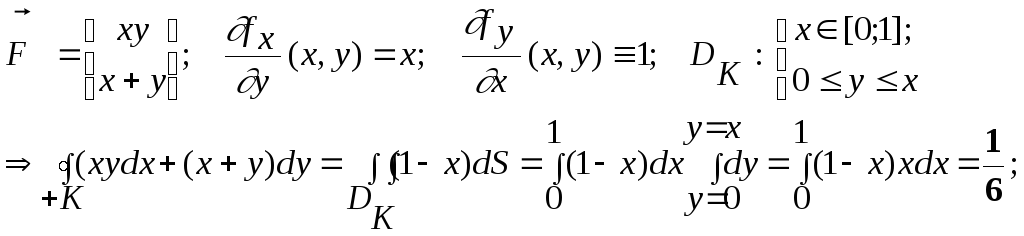
Убедитесь самостоятельно, что

2) §3 Независимость к.И. От пути; потенциальное векторное поле и его потенциал.

Если формула Грина 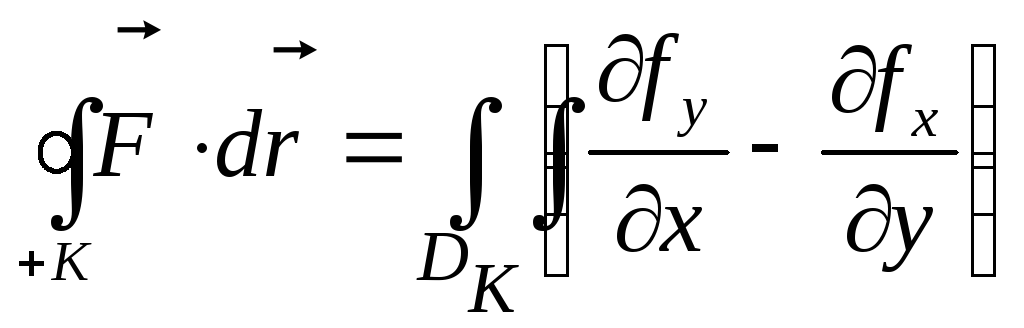верна для области D_К ÌR² , она верна для любого контура К₁D_K , целиком лежащего в области. Кроме того,

Следствия. Если плоское векторное поле F=[f_x; f_y] удовлетворяет условию

, то

1. КИ по любому замкнутому контуру, целиком лежащему в области, равен нулю.

2. КИ по гладкой линии LÌD, соединяющей точки А, В , не зависит от формы линии , определяется только положением точек А и В на плоскости

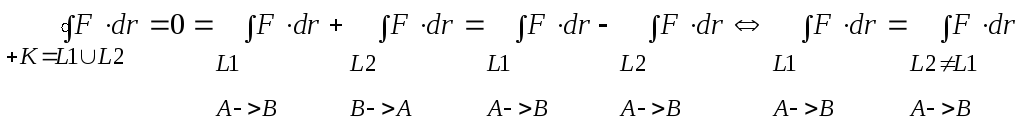=U(B)-U(A)

и равен разности значений некоторой функции U(x,y) в этих точках.

Определение. Плоское векторное поле, криволинейный интеграл в котором не зависит от формы пути, называется потенциальным векторным полем, а функция U(x,y) называется потенциалом векторного поля.

Замечания.

1) Работа в потенциальном силовом поле равна разности потенциалов поля в начальной и конечной точках.

3. В математической «триаде»: 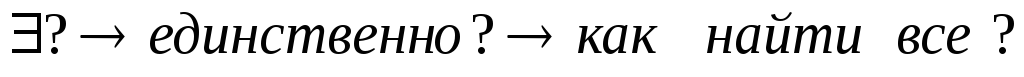для потенциала векторного поля ответ на первый вопрос дает теорема Грина: «Всякое непрерывно дифференцируемое плоское векторное поле F(x,y)=[f_x;f_y]^t, удовлетворяющее условию 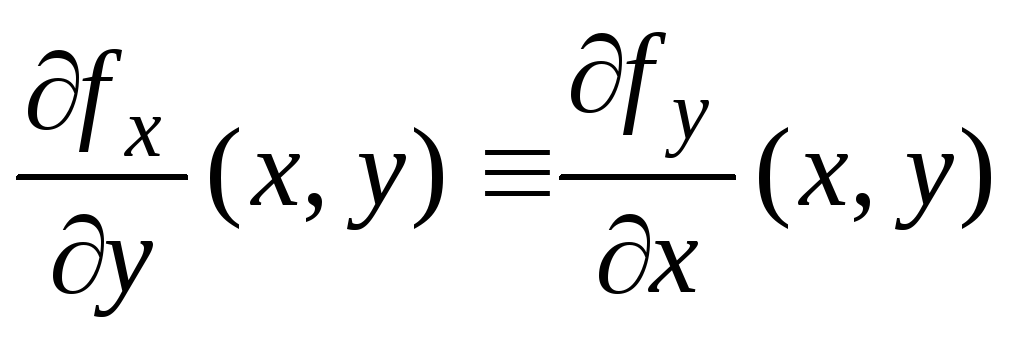, имеет потенциал – скалярную функциюU(x,y)».

Для ответа на два другие вопроса рассмотрим дважды непрерывно дифференцируемую функцию двух переменных

Таким образом, дважды непрерывно дифференцируемая функция U(x,y) “порождает” потенциальное векторное поле .

Верно и обратное утверждение: потенциал U(x,y) потенциального плоского векторного поля F=[f_x;f_y] является решением системы дифференциальных уравнений в частных производных:

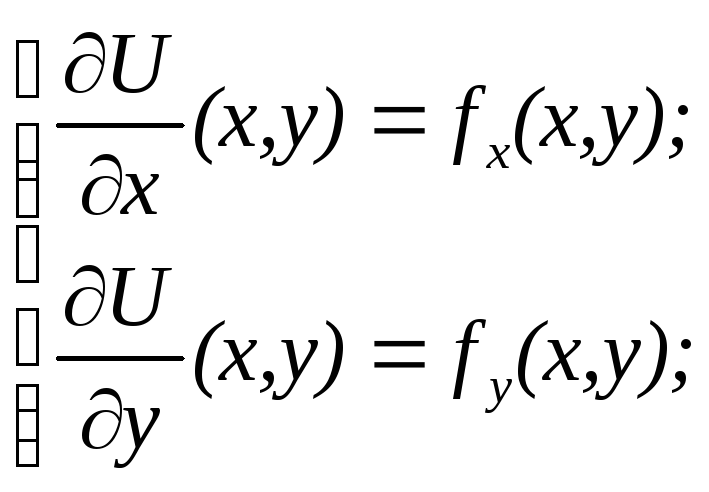
Найдем решение этой системы.

1. Из определения частной производной функции следует:

Таким образом, “частное” интегрирование одного из уравнений позволяет найти потенциал с точностью до “произвольной” дифферецируемой функции другой переменной. (2) после этого второе уравнение позволяет найти потенциал с точностью до аддитивной произвольной константы:

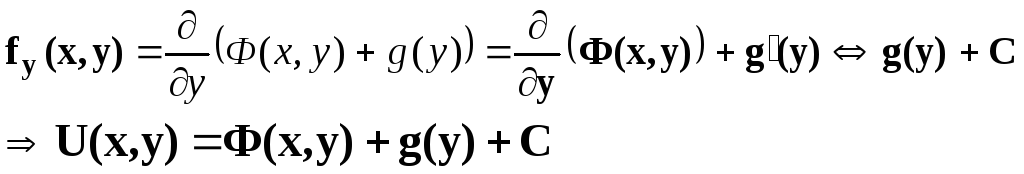
Пример. F=[xy;x²/2+y]^t : ¶f_x/¶y º ¶f_y/¶x º x; - поле потенциальное !! Найдем его потенциал.


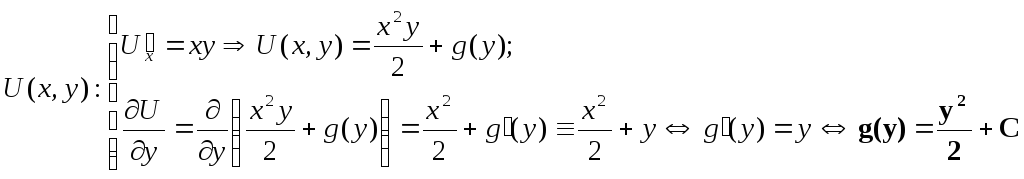