4.Масштабирование.

Пусть f(x) имеет вид:, где a_i>0 сильно различаются между собой. Поверхности уровней функции вытянуты вдоль тех осей x_i, которым соответствуют малые a_i.

Для более эффективного применения градиентных методов необходимо превращение поверхностей уровня в круги

x₀

Заменой переменных можно добиться того, чтобы у новых переменных y_i поверхности уровней стали сферами. Для этого достаточно принять (все коэффициенты квадр. формы- единицы)

В случае, когда f(x) не квадратичная, а достаточно гладкая функция общего вида выбирают:

Это диагональные элементы матрицы вторых производных. Это преобразование не превратит поверхности уровня в сферы, но в некоторых случаях позволит уменьшить их вытянутость. Гарантировано исправить топографию функции f(x) можно, если учесть все, а не только диагональные элементы матрицы вторых производных и преобразования координат вида:

1.2 Метод Ньютона.

Разложим f(x) в ряд Тейлора до 2-го слагаемого включительно:

(*)

- вектор

- матрица Гессе, матрица вторых производных.

Будем рассматривать квадратичную аппроксимацию f(x) тогда получим (*) без то есть предполагаем, что f(x) квадратичная форма. Эта форма имеет единственную точку min, который является корнем уравнения f ’(x)=0.

В данном случае:

Метод Ньютона

Пример:

Сделаем одну итерацию метода Ньютона для квадратичной функции

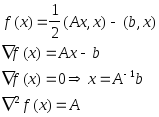
Этот пример показывает связь решения системы уравнений Ax-b = 0 и поиска минимума соответствующей функции f(x).

= A - матрица вторых производных.

Одна итерация метода Ньютона:

Но это точка минимума квадратичной функции. Таким образом для квадратичной функции метод Ньютона сходится за один шаг (матрица А должна быть положительно определена и симметрична, значения собственных чисел (растянутость) не играют роли).

Точка х₁ гораздо ближе к х* , чем в градиентных методах, но надо вычислить матрицу Гессе и обратить ее. Градиентный метод медленнее, но без дополнительных вычислений.

Оценим скорость сходимости метода Ньютона:

Теорема (о скорости сходимости метода Ньютона):

Пусть f(x) дважды дифференцируема, матрица удовлетворяет условию

Липшица с константой L :

f(x) сильно выпукла: 0 l I ² f(x) и начальное приближение удовлетворяет условию:

Тогда метод Ньютона сходится х* с квадратичной скоростью

Доказательство:

Известно, что:

1)

Если на g’(x) удовлетворяет условию Липшица , то

Применим это отношение к ² f(x), тогда

Пусть x = x_k , тогда

Дано (см. условие)тогда:

Таким образом .

Пусть q₁= (обозначим). Рассмотрим полученное неравенство

.........................................................................

Для сильно выпуклых функций известно

Тогда

Теорема доказана.

Если начальные условия не удовлетворяют требованиям теоремы, то метод может не сходиться.

Пусть метод обеспечивает выполнение следующего неравенства

, где d- наибольшее из чисел, для которых выполняется это условие, тогда d- скорость сходимости метода.

Если обозначить _k = ,тогда скорость сходимости

d = , при_k0 (k ).

Пусть _k+1q _k, 0 q 1. Для этого случая d =1- линейная скорость. Для метода Ньютона тогда _k+1= const _k²  d =2- поэтому скорость называется квадратичной.