2.2.1. Определение положений

План положений механизма – это графическое изображение взаимного расположения звеньев, соответствующее выбранному расчетному положению начального звена.

План положений механизма для угла = показан на рис. 2.1. Масштабный коэффициент плана положений определяется как

(2.22)

где - действительная длина звена 1; - длина отрезка, изображающего звено 1 на плане положений.

Тогда отрезок , соответствующий длине звена 2, будет

(2.23)

План положений позволяет определить угол и координаты точек и :

(2.24)

Для рассматриваемого примера численные значения приведенных параметров будут следующие:

м/мм;

мм;

; м; м; м.

Значения , , , с большой степенью точности приближены к значениям, полученным аналитическим способом.

2.2.2. Определение скоростей

Метод основан на графическом решении векторных уравнений движения. Для построения плана скоростей должна быть известна кинематическая схема механизма, построенная в масштабе (рис. 2.2, а), и задан закон движения начального звена (например, ).

Требуется найти линейные скорости точек , и , а также угловую скорость звена 2.

Построение плана скоростей начинается с определения скорости точки кривошипа

(2.25)

Вектор скорости точки направлен перпендикулярно кривошипу в направлении его вращения.

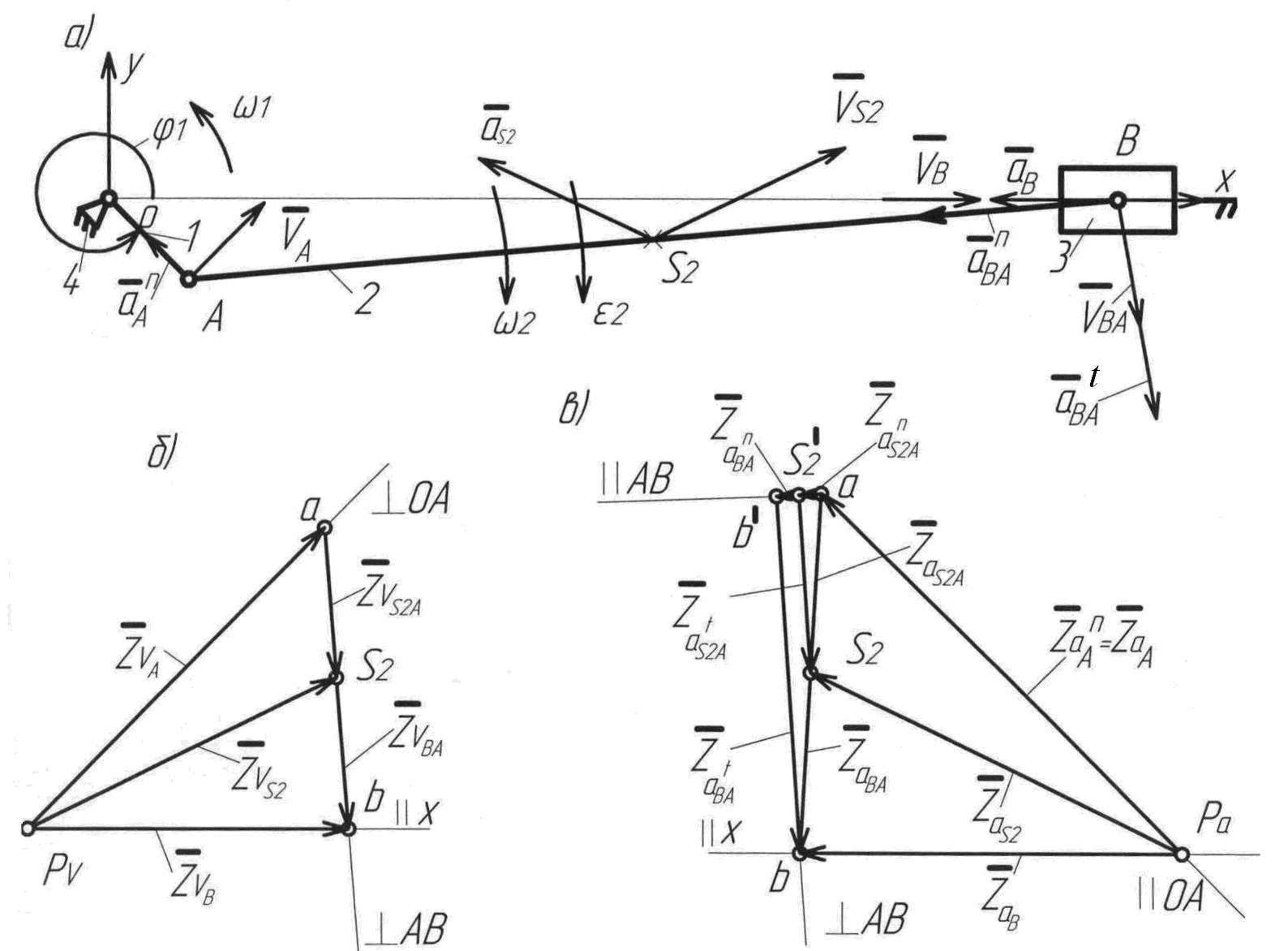
Рис.2.2. Схема механизма, планы скоростей и ускорений

Скорость точки , принадлежащей звену 2, можно представить как векторную сумму скоростей переносного и относительного движений

(2.26)

Переносным движением звена 2 является поступательное движение его со скоростью точки

а относительным – вращательное движение звена 2 вокруг точки А. Если обозначить относительную скорость через , то

Окончательно векторное уравнение для скорости точки В будет иметь вид

(2.27)

В этом уравнении векторы скоростей, известные по величине и направлению, подчеркнуты двумя чертами, а известные лишь по направлению – одной чертой.

Для определения указанных неизвестных величин строим план скоростей с выбранным масштабным коэффициентом

(2.28)

Здесь

- длина отрезка, изображающего на плане скорость .

Из произвольной точки полюса плана скоростей (рис. 2.2, б) проведем вектор , перпендикулярный кривошипу ОА, соответствующий на плане скоростей абсолютной скорости . Из конца вектора (точка а) проводим линию в направлении относительной скорости , перпендикулярную , а из полюса - линию в направлении скорости , параллельную . В пересечении указанных линий находим точку b. Вектор изображает скорость точки В, а вектор - скорость . Величины действительных скоростей определяют по формулам

Направление скорости определяется при параллельном переносе вектора в точку В механизма (рис. 2.2, а). Т.к. вектор в точке В механизма направлен в сторону положительной полуоси , знак скорости будет положительным.

Модуль угловой скорости звена 2 будет

(2.29)

Направление находится по вектору . На рис. 2.2, а направлена по часовой стрелке.

Скорость точки определяется с помощью векторного уравнения:

(2.30)

Здесь скорость относительного движения точки находится методом пропорционального деления отрезка ав на плане скоростей, изображающего относительную скорость

(2.31)

Действительная скорость определяется как

(2.32)

Для рассматриваемого примера численное значение скорости равно

=12,56*0,175=2,198 м/с 2,2 м/с.

Если на плане скоростей (рис.2.2,б) известную скорость изобразить отрезком длиной 66 мм, то получим:

=51 мм; =47 мм;

м/с.

Так как вектор в точке В механизма направлен в сторону положительной полуоси ,знак будет положительным:

=1,7 м/с

м/с; .

Угловая скорость направлена по часовой стрелке, поэтому имеет знак «минус»:

1/с;

мм; м/с.

Сравнение с результатами аналитического метода расчета дает ошибку не более 3%.