3.1 Статические моменты сечения.

Статистическим моментом сечения, относительно некоторой оси, называется взятая по всей площади А сумма произведений элементарных площадок dА на их расстояния до этой оси (рис. 3.1).

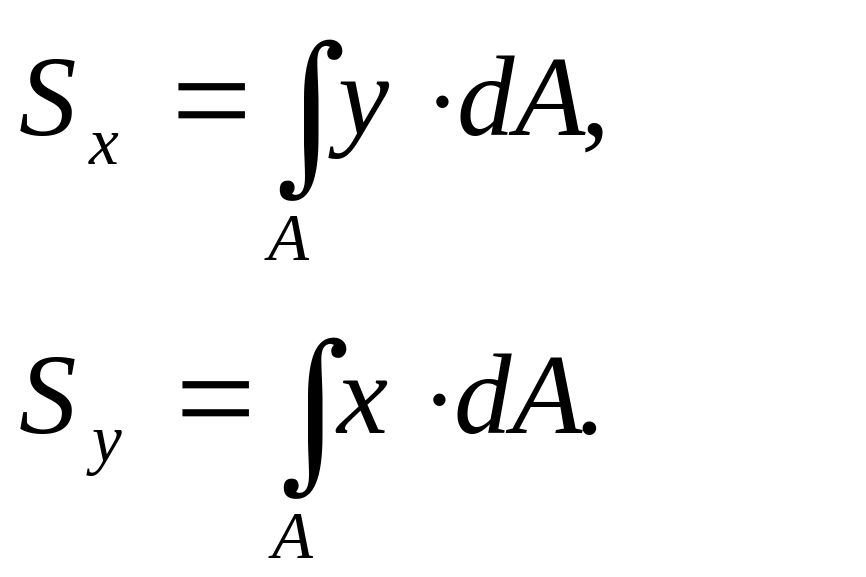[м³] , [см³] (3.1)

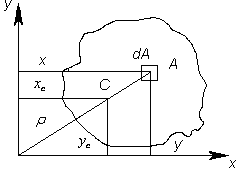
Рис 3.1

При параллельном переносе осей статический момент меняется на величину, равную произведению площади на расстояние между осями.

Ось, относительно которой статистический момент равен нулю, называется центральной. Точка пересечения центральных осей называется центром тяжести сечения (рис.3.2).

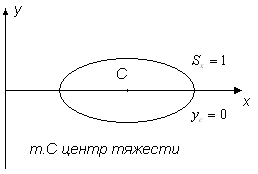
Рис 3.2

Статистический момент относительно любой оси, проходящей через центр тяжести, равен нулю.

Из определения статистического момента сечения получим формулы для определения центра тяжести сечения:

( 3.2)

Если положение центра тяжести сечения известно, а требуется определить статистические моменты сечения относительно любых осей х и у, то используются следующие формулы:

(3.3)

Согласно формулам (3.3) статический момент площади А относительно какой-либо оси равен произведению всей площади А на расстояние от ее центра тяжести до этой оси.

Если сечение имеет сложную форму, то его разбивают на отдельные элементы и координаты центра тяжести вычисляют по формулам:

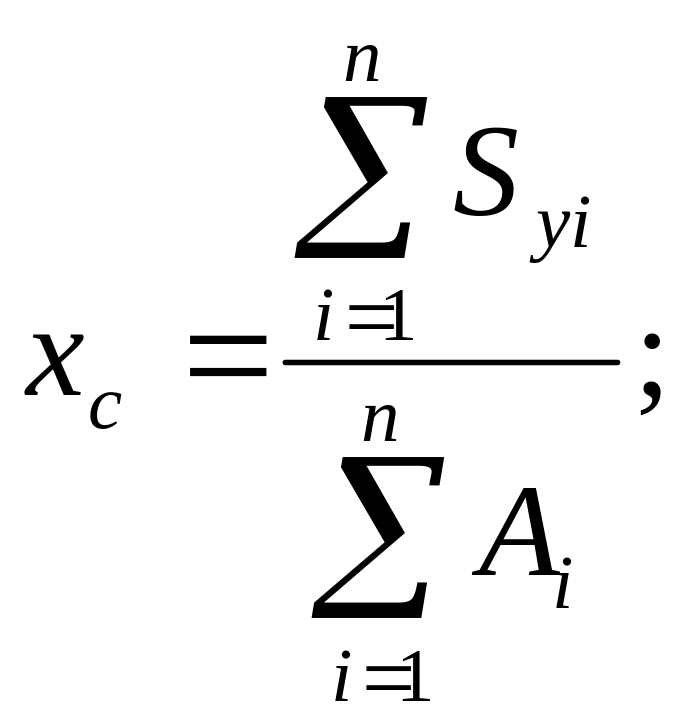
(3.4)

3.2 Моменты инерции сечений.

Осевым моментом инерции сечения относительно некоторой оси называется взятая по всей его площади А сумма произведений элементарных площадок dА на квадраты их расстояний до этой оси:

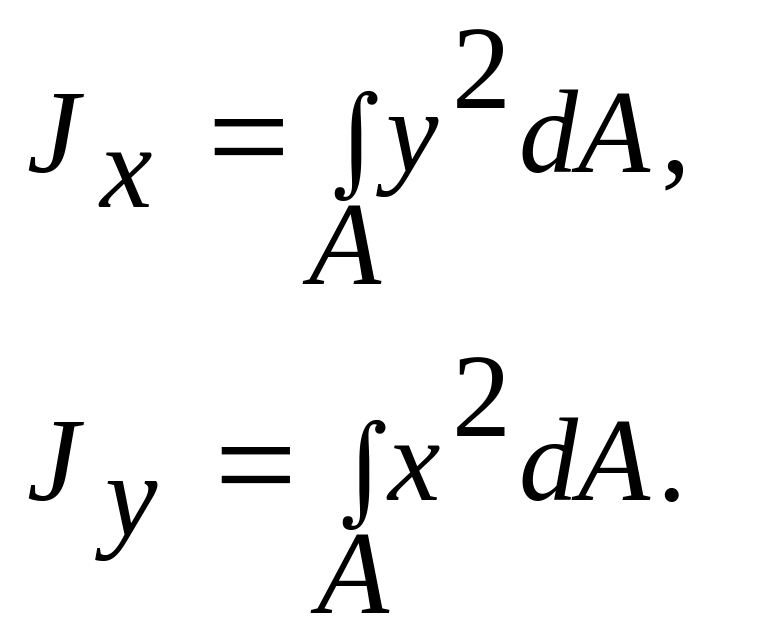(3.5)

Центробежным моментом инерции сечения относительно некоторых двух взаимно перпендикулярных осей называется взятая по всей его площади А сумма произведений элементарных площадок dА на расстояние до этих осей:

(3.6)

Центробежный момент может быть положительным, отрицательным и равным нулю.

Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятая по всей его площади А сумма произведений элементарных площадок dА на квадраты их расстояний до этой точки:

(3.7)

Осевые и полярные моменты инерции всегда положительны.

По теореме Пифагора (см. рис. 3.1), следовательно:

(3.8)

Согласно (3.8) сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей равна полярному моменту инерции этого сечения относительно точки пересечения указанных осей.

При вычислении моментов инерции сложной фигуры, она разбивается на отдельные элементарные фигуры, находятся моменты инерции каждой фигуры относительно выбранной оси и результаты складываются. Можно складывать только моменты инерции различных фигур, определенных относительно одной и той же оси!

3.3 Определение моментов инерции при параллельном переносе координатных осей.

Выведем формулы преобразования моментов инерции при параллельном переносе осей. Пусть известны геометрические характеристики сечения А относительно произвольных осей x,y. Оси x₁, y₁ параллельны осям x,y (рис.3.3).

Дано:

а, b – расстояния между осями x, x₁ и y, y₁.

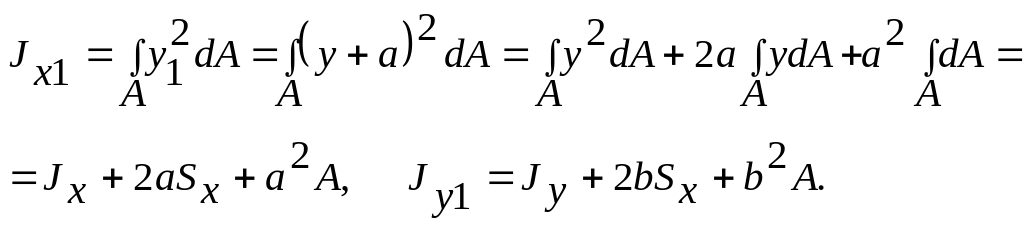(3.9)

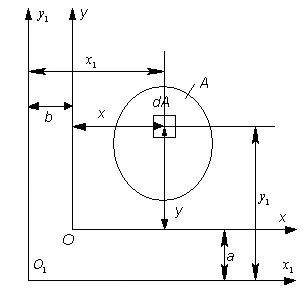
Рис.3.3

Если оси х и у центральные, то , следовательно:

(3.10)

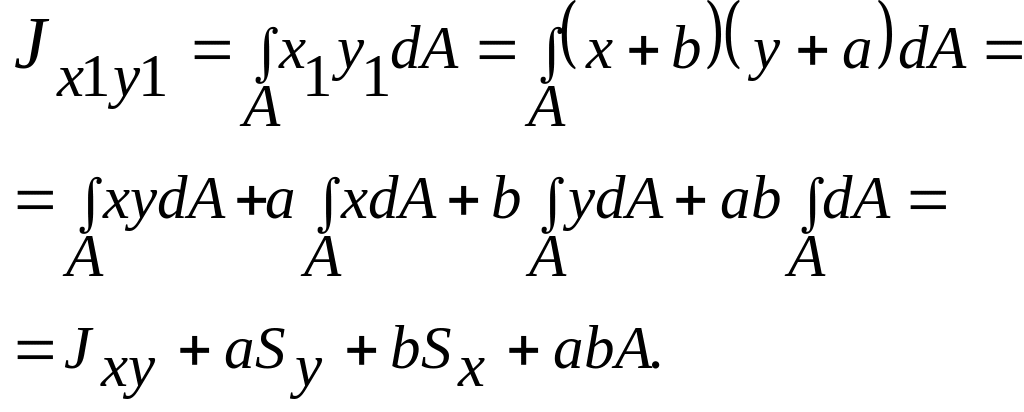(3.11)

Если оси х и у – центральные, то,

(3.12)

Из формул (3.10), (3.12) следует, что в семействе параллельных осей минимальный момент инерции получается относительно центральных осей ( а=0 и b=0 ).

При переходе от центральных осей к нецентральным осевые моменты увеличиваются на величину и , а при переходе от нецентральных к центральным уменьшаются на те же величины. Для центробежного момента следует учитывать знак величин а и b.