
- •Введение
- •Глава 1. Основные понятия науки о сопротивлении материалов
- •1.1 Цели и задачи сопротивления материалов
- •1.2 Расчетная схема и классификация элементов конструкций по геометрическим признакам.
- •1.2 Формы стержней: а) прямой; б) кривой.
- •1.3 Классификация нагрузок
- •1.4 Внутренние усилия. Метод сечений
- •1.4 Напряжения и деформации
- •1.6 Гипотезы науки о сопротивлении материалов
- •Контрольные вопросы:
- •Тестовые задания по главе 1
- •Глава 2. Построение эпюр внутренних усилий
- •2.1 Построение эпюры продольной силы
- •Порядок построения эпюры продольной силы (n)
- •Проверка правильности построения эпюры продольной силы.
- •2 .2 Построение эпюры крутящего момента
- •2.3 Построение эпюр поперечной силы Qу и изгибающего момента Мx
- •Порядок построения эпюр Qу и мх
- •Проверка правильности построения эпюр Qу и мх
- •Контрольные вопросы:
- •Тестовые задания по главе 2:
- •Глава 3. Геометрические характеристики плоских сечений
- •3.1 Статические моменты сечения.
- •3.2 Моменты инерции сечений.
- •3.3 Определение моментов инерции при параллельном переносе координатных осей.
- •3.4 Определение моментов инерции при повороте координатных осей.
- •3.5 Моменты инерции элементарных фигур.
- •3.6 Порядок нахождения главных центральных моментов инерции и положения главных осей для сложных сечений.
- •Контрольные вопросы:
- •Тестовые задания к главе 3
- •Глава 4. Осевое растяжение (сжатие) прямого бруса.
- •4.1 Определение напряжений и деформаций при осевом растяжении (сжатии).
- •4.2 Основные механические характеристики материла.
- •4.3 Допускаемые напряжения. Условие прочности.
- •4.4 Напряжения на площадках наклонных к оси.
- •Контрольные вопросы:
- •Тестовые задания к главе 4:
- •Глава 5. Сдвиг и кручение
- •5.1 Чистый сдвиг
- •5.2 Закон Гука для чистого сдвига.
- •5.3 Расчет заклепочных соединений
- •5.4 Расчет сварных соединений
- •5.5 Напряжения и деформации при кручении
- •5.6 Расчет на прочность и жесткость при кручении
- •Три типа задач расчета на прочность при кручении.
- •5.7 Анализ напряженного состояния и разрушения вала при кручении
- •Расчет валов на кручение
- •Контрольные вопросы:
- •Тестовые задания к главе 5
- •Глава 6. Напряженное состояние в точке. Теории прочности
- •6.1 Напряженное состояние в точке
- •6.2 Теории прочности
- •Контрольные вопросы:
- •Тестовые задания к главе 6
- •Глава 7. Изгиб
- •7.1 Определение напряжений при чистом изгибе.
- •7.2 Расчет балок по нормальным напряжениям.
- •7.3 Определение напряжений при поперечном изгибе.
- •Полный расчет балки на изгиб.
- •Контрольные вопросы:
- •Тестовые задания к главе 7
- •Глава 8. Продольный изгиб.
- •8.1 Понятие устойчивого и неустойчивого равновесия
- •8.2 Формула Эйлера для определения критической силы.
- •8.3 Влияние способа закрепления концов стержня на величину
- •8.4 Предел применимости формулы Эйлера.
- •8.5 Практические расчеты на устойчивость.
- •Контрольные вопросы:
- •Тестовые задания к главе 8
- •Задания к самостоятельной контрольной работе
- •Задача № 1 Геометрические характеристики плоских сечений
- •Расчетные схемы к задаче №1
- •Задача № 2 Расчет ступенчатого бруса
- •Расчетные схемы к задаче №2
- •Задача № 3 Расчет вала на кручение.
- •Расчетные схемы к задаче №3
- •Задача № 4 Расчет балки на изгиб.
- •Расчетные схемы к задаче №4
- •Задача № 5 Расчет бруса на совместное действие изгиба и кручения.
- •Расчетные схемы к задаче №5
- •Задача № 6 Расчет на устойчивость
- •Расчетные схемы к задаче №6
- •Литература рекомендуемая для решения контрольной работы
- •Сортамент прокатной стали Балки двутавровые горячекатаные (по гост 8239-93, выборка)
- •Швеллер стальной горячекатаный (гост 8240, выборка)
- •Уголки стальные горячекатаные равнополочные (гост 8509-93, выборка)
- •Библиографический список
- •Оглавление
- •Глава1. Основные понятия науки о сопротивлении материалов.
- •Глава 2. Построение эпюр внутренних усилий.
- •Глава 3. Геометрические характеристики плоских сечений.
1.4 Внутренние усилия. Метод сечений
Между частицами твердого тела до приложения нагрузок действуют силы, обеспечивающие неизменность его формы. Они называются внутренними усилиями. При действии на тело внешних сил оно деформируется, следовательно, меняется взаимное расположение частиц и внутренние усилия изменяются.
В сопротивлении материалов применяется гипотеза о ненапряженном начальном состоянии тела, т.е. учитываются только внутренние усилия, возникающие при нагружении тела.
Для оценки прочности конструкции необходимо уметь определять значение и направление внутренних усилий. Для этого пользуются методом сечений, который заключается в следующем:
тело, находящееся под действием внешних сил рассекается плоскостью в нужном месте и рассматривается равновесие одной из отсеченных частей, либо левой, либо правой. Для этого составляются уравнения равновесия рассматриваемой отсеченной части с учетом внутренних усилий, возникающих в сечении.
Внутренние усилия, выявляемые в сечениях, в соответствии с принципом действия и противодействия, всегда равны по величине и противоположны по направлению.
В соответствии с правилами статики приведем систему внутренних усилий, действующих на одну из отсеченных частей к центру тяжести сечения. В результате получим главный вектор R и главный момент M.
В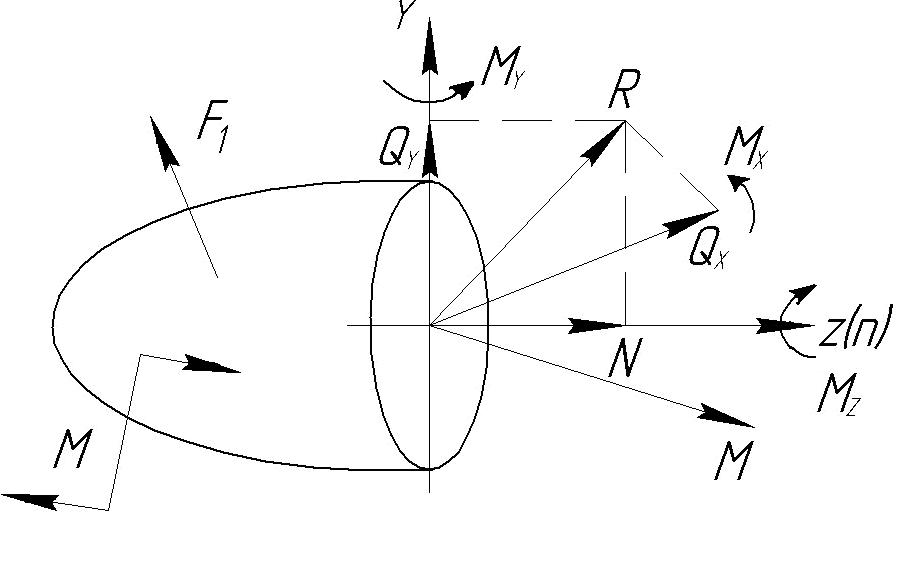 ыберем
систему координат x,y,z
с началом
координат в центре тяжести сечения.
Разложим главный вектор и главный момент
по осям координат. В результате получим
шесть составляющих, которые называют
внутренними
силовыми факторами (рис.1.11).
ыберем
систему координат x,y,z
с началом
координат в центре тяжести сечения.
Разложим главный вектор и главный момент
по осям координат. В результате получим
шесть составляющих, которые называют
внутренними
силовыми факторами (рис.1.11).
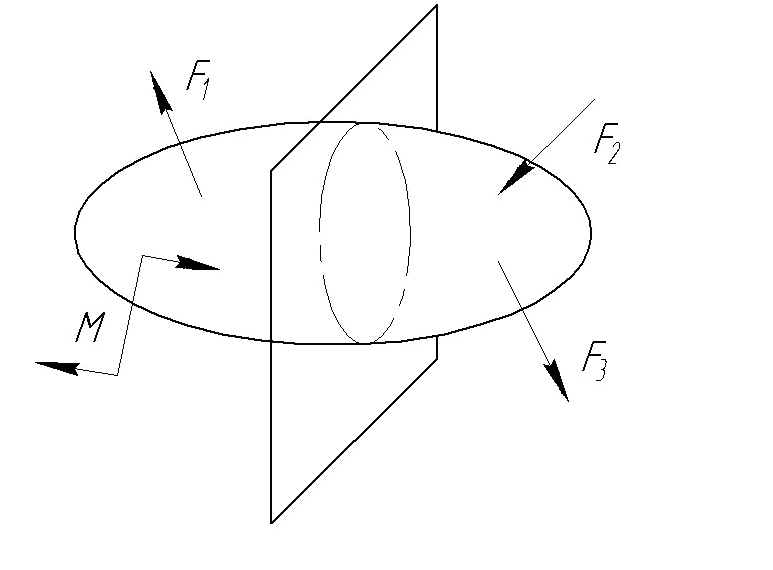
Рис 1.11
Главный вектор и главный момент определяются по формулам:
![]() ,
(1.1)
,
(1.1)
![]() ,
(1.2)
,
(1.2)
где, N – нормальная (продольная) сила, Qx и Qy - поперечные силы, Мz - крутящий момент, Мx и Мy – изгибающие моменты.
При известных внешних силах эти шесть силовых фактора находят из шести уравнений равновесия, составленных для отсеченной части стержня:
![]()
![]()
![]()
1.4 Напряжения и деформации
Внутренние усилия не являются критериями, позволяющим рассчитать элемент конструкции на прочность. Таким критерием является напряжение.
Зафиксируем точку в рассматриваемом сечении А. В окрестности этой точки выделим малую площадку ∆А. Главный вектор внутренних сил, действующих на этой площадке, обозначим через ∆R (рис. 1.12 а).
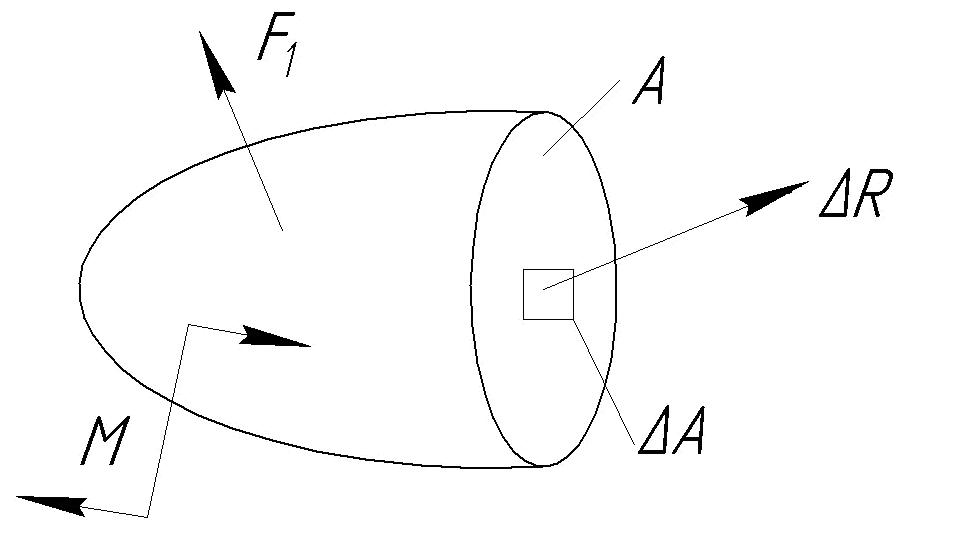
а) б) Рис.1.12
Тогда
![]() есть среднее напряжение на площадке
∆А. Полное
напряжение в точке сечения А
будет определяться пределом:
есть среднее напряжение на площадке
∆А. Полное
напряжение в точке сечения А
будет определяться пределом:
![]() .
(1.3)
.
(1.3)
Введенный таким образом вектор р называется вектором напряжений в точке. Этот вектор зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки ∆А, характеризуемой вектором п. Совокупность всех векторов напряжений в точке для всевозможных направлений вектора п определяет напряженное состояние в этой точке.
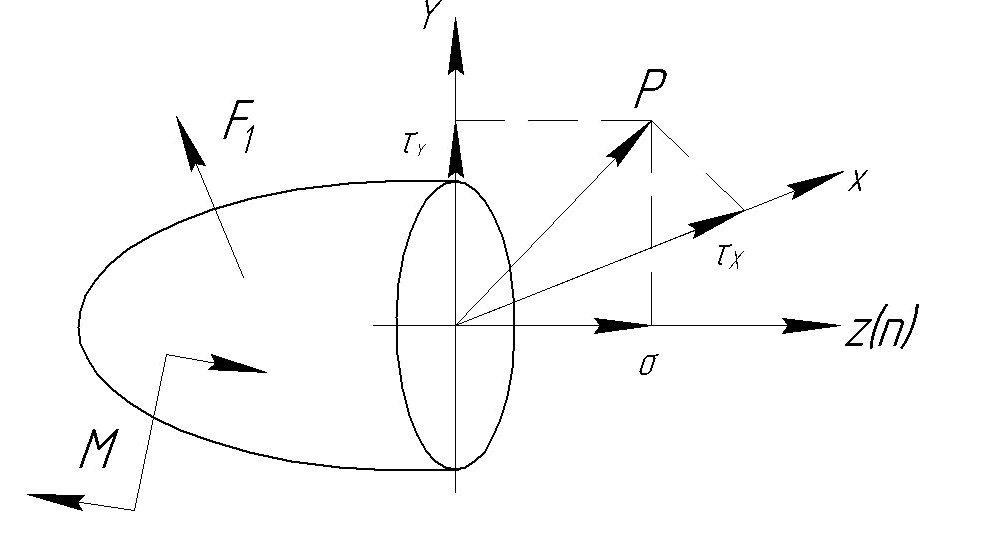
При разложении вектора напряжений по осям координат получим (рис. 1.12, б):
![]() (1.4)
(1.4)
где
![]() –
нормальное напряжение;
–
нормальное напряжение;
![]() и
и
![]() -
касательные напряжения.
-
касательные напряжения.
Размерность напряжений равна отношению размерности силы к размерности площади. В международной системе единиц СИ напряжения измеряются в паскалях: 1 Па=1 Н/м2.
Растягивающее нормальное напряжение является положительным. Сжимающее нормальное напряжение является отрицательным.
Касательное напряжение является положительным, если оно вращает рассматриваемый элемент, относительно внутренней нормали по часовой стрелке и наоборот.
Через точку можно провести множество площадок, напряжения на которых будут различными.
При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела.
Отнесем недеформированное тело к декартовой системе координат xyz (рис. 1.14). Положение некоторой точки М в этой системе координат определяется радиус-вектором r(х, у, z). В деформированном состоянии точка М займет новое положение М/, характеризуемое радиус-вектором r' (х, у, z). Вектор u=r'—r называется вектором, перемещений точки М. Проекции вектора u на координатные оси определяют компоненты вектора перемещений и(х, у, z), v(х, у, z), w(х, у, z), равные разности декартовых координат точки тела после и до деформации.
Перемещение, при котором взаимное расположение точек тела не меняется, не сопровождается деформациями. В этом случае говорят, что тело перемещается как жесткое целое (линейное перемещение в пространстве или поворот относительно некоторой точки). С другой стороны, деформация, связанная с изменением формы тела и его объема, невозможна без перемещения его точек.
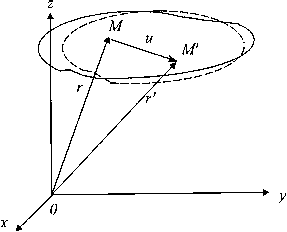 Рис.1.14
Вектор перемещения
Рис.1.14
Вектор перемещения
Деформации
тела характеризуются изменением
взаимного расположения точек тела до,
и после деформации. Рассмотрим, например,
точку М
и близкую к ней точку N,
расстояние между которыми, в
недеформированном состоянии вдоль
направления вектора s обозначим через
∆S
(рис.
1.15). В деформированном состоянии точки
М
и N
переместятся в новое положение (точки
М'
и N’),
расстояние между которыми обозначим
через
![]() s'.
Предел отношения
s'.
Предел отношения
![]() (1.5)
(1.5)
называется относительной линейной деформацией в точке М в направлении вектора s. Рассматривая три взаимно перпендикулярных направления, например, вдоль координатных осей Ох, Оу и Oz, получим три компоненты относительных линейных деформаций εx, εy, εz, характеризующих изменение объема тела в процессе деформации.
Для описания деформаций, связанных с изменением формы тела, рассмотрим точку М и две близкие к ней точки N и Р, расположенные в недеформированном состоянии в направлении двух взаимно ортогональных векторов s1 и s2. Расстояния между точками обозначим через ΔS1и ΔS2 (рис. 1.16). В деформированном состоянии положение точек обозначим через М', N' и Р'. Угол между отрезками M'N' и М'Р' в общем случае будет отличным от прямого. При ΔS1→0, ΔS2→0 изменение угла γ12 между двумя ортогональными до деформации направлениями называется угловой деформацией. Как видно из рис. 1.16, угловая деформация складывается из двух углов α1и, α2 связанных с поворотами отрезков M’N' и М'Р' 'в.плоскости, образованной векторами s1 и s2, относительно этих векторов. Если заданы три взаимно ортогональных вектора, направленных вдоль координатных осей, то имеются три угловые деформации γxy, γxz и yγz, которые вместе с тремя линейными деформациями εx, εy, εz, полностью определяют деформированное состояние в точке.
 Рис.1.15
Линейная деформация
Рис.1.15
Линейная деформация
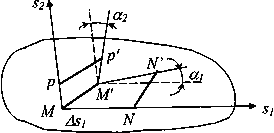 Рис.
1.16 Угловая деформация
Рис.
1.16 Угловая деформация
Совокупность линейных деформаций по всем направлениям и угловых деформаций по всем плоскостям, проведенных через точку образуют деформированное состояние этой точки.
