I. Сглаживание кривой заданного порядка.

Маткад позволяет вычислять нелинейную регрессию несколькими способами.

1.При сглаживании одной кривой функция regress(vx,vy,n) вычисляет и представляет в векторе vs коэффициенты полинома, наилучшим образом сглаживающего исходные данные. Степень полинома задается числом n. По этим коэффициентам функция интерполяции interp вычисляет точки аппроксимирующей кривой.

На рис. 2 показано использование этих двух функций для того же набора данных, что и в случае линейной регрессии при сглаживании кривой третьего порядка (При решении примера необходимо ввести вектора vx и vy).

Задача.3. Решите в Маткаде приведенную на рис.2 задачу.

Рис.2.Сглаживание кривой третьего порядка

Решите ту же задачу для линейного, квадратичного сглаживания функцией regress, а также для сглаживания кривой четвертого порядка

Сглаживание заданным набором кривых.

Часто одной функции недостаточно, чтобы удовлетворительно провести аппроксимацию.

Маткад позволяет с помощью функции linfit проводить аппроксимацию набором кривых, заданных вектором f.

На рис.3. приведен набор функций и проведена аппроксимация тех же данных, что и в предыдущих задачах, набором полиномов.

Сначала, для проведения сортировки формируется матрица М и проводится сортировка. Затем формируются отсортированные вектора vx и vy.

Набор полиномов задается функцией f(х)

Используя функцию linfit, Маткад формирует вектор а, умножение которого на f(x) и дает аппроксимирующую кривую.

Рис.3 Аппроксимация набором функций

Задача 4 . Решите в Маткаде пример рис.3

Задача 5. Подберите набор функций для следующих данных :

X	5	1	3	8	9	2	4	6	7
y	0.5	9.1	3.4	5.7	2.9	3.6	7.1	6.7	0

Множественная регрессия.

В Маткаде возможна реализация множественной регрессии с помощью встроенных функций только для двух аргументов. Множественная регрессия при большем их числе может быть реализована с помощью функции minerr (minimum error – минимальная ошибка).

Множественная регрессия двух аргументов реализуется в Маткаде с помощью функции regress( M, vz, n)

Функция regress возвращает координаты аппроксимирующей поверхности.

Здесь М - матрица 2*m из двух столбцов и m строк, в которую заносятся наблюденные данные двух аргументов, vz- вектор наблюденных значений аппроксимируемой функции,

14. степень приближающего полинома. При n=1 имеем линейную, при n >1 - нелинейную множественную регрессию.

Аппроксимация плоскостью.

Задана матрица аргументов M и вектор наблюдений vz (См. рисунок 4). Вектор vs определяет коэффициенты аппроксимирующей плоскости. Здесь нижний элемент – коэффициент при х, следующий – коэффициент при у, а третий снизу – свободный член.

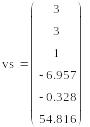
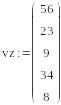
Рис.4. Исходные данные вычисление вектора vs

Составляем уравнение плоскости

Теперь, как всегда при формировании трехмерного графика создаем матрицу решений и строим график или (и) получаем таблицу решений в узловых точках.

Рис.5. График линейной множественной регрессии.

Нелинейная аппроксимация полиномом 2-го порядка.

Рис.6. Построение множественной нелинейной регрессии с использованием функции regress.

На рисунке 6 приведена регрессия с помощью функции regress полиномом второго порядка. Заданы М, vz из десяти значений. Принимаем n=2.

В векторе vs вычислены коэффициенты аппроксимирующего полинома второго порядка. Здесь. Первый снизу элемент вектора – коэффициент полинома при х², Второй снизу – коэффициент при х, третий снизу – свободный член, четвертый – коэффициент при у, пятый – при ху и шестой – при у^2.

Т аким образом аппроксимирующая функция имеет вид :

Обычным способом получаем таблицу решений и строим график (рис.7) этой функции :

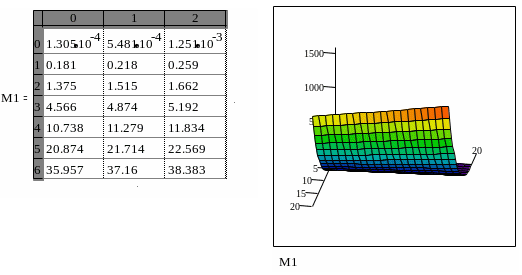Рис.7. График нелинейной регрессии.

Недостатком изложенного метода является необходимость изменения уравнения при изменении условий задачи. Кроме того, в доступных книгах по Маткаду не приводится расшифровка коэффициентов полинома в векторе vs , а их экспериментальная расшифровка для полиномов высокого порядка затруднительна.

Множественная регрессия с использованием функции « MINERR».

Как уже говорилось, построение регрессии с использованием функции minerr производится в случае размерности регрессии более двух. При этом используется блок решения given. Ниже на рис.8 приведено построение множественной, четырехмерной, т.е. в функции четырех аргументов линейной регрессии.

В матрице М – экспериментальные значения аргументов, в векторе vy – экспериментальные значения функции. Функция y аппроксимируется функцией y_i. Заданы начальные приближения для аппроксимирующих коэффициентов a,b,c,d,k.

В решающем блоке given строится выражение для квадрата разностей между экспериментальными значениями вектора vy и аппроксимирующей функцией у. В процессе решения методом наименьших квадратов определяются коэффициенты аппроксимирующей функции у.

Рис.8 Вычисление множественной линейной регрессии с помощью функции minerr.

Множественная нелинейная регрессия с MINERR.

При решении задач нелинейной регрессии, как и при решении любых нелинейных задач, следует учитывать зависимость ответа от заданных начальных приближений.

Задача. Исходные данные по аргументам заданы матрицей М, исходные данные для функции – вектором vy. Задаемся начальными приближениями коэффициентов.

Рис.9. Исходные данные для вычисления нелинейной множественной регрессии.

В качестве аппроксимирующего выбираем полином с неопределенными показателями степеней. Значения этих показателей должны быть также определены в процессе расчета.

Составляем выражение для метода наименьших квадратов в решающем блоке given

Рис.10. Вычисление нелинейной множественной регрессии с помощью функции minerr.

ЛАБОРАТОРНАЯ РАБОТА №6. ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ И ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ.

Доверительной областью называется область, внутри которой случайная величина находится с вероятностью не менее заданной, а доверительным интервалом – границы этой области.

Задача 1. Произведено 20 опытов над величиной Х . Результаты приведены в таблице:

i	xi	i	xi
1	10.5	11	10.6
2	10.8	12	11.3
3	11.2	13	10.5
4	10.9	14	10.7
5	10.4	15	10.8
6	10.6	16	10.9
7	10.9	17	10.8
8	11.0	18	10.7
9	10.3	19	10.9
10	10.8	20	11.0

Требуется .найти оценку математического ожидания и и построить для него доверительный интервал вероятности β=0.8.

1.Составляем из таблицы вектор X (на рис.1 для экономии места часть этого вектора приведена в транспонированном виде). Вычисляем с помощью встроенной функции mean среднее арифметическое – оценку математического ожидания, а с помощью встроенной функции stdev – оценку среднеквадратического отклонения. .

Рис.1 Ввод наблюдений и вычисление числовых характеристик.

Вычисленное значение среднего является случайной величиной (например, если увеличить число опытов, то оно изменится). И как для любой случайной величины, мы можем построить для него математическое ожидание и среднеквадратическое отклонение.

Теперь мы должны найти для него такой отрезок на оси х, внутри которого эта случайная величина находится с вероятностью 0,8.

Для решения этой задачи нужно найти такой интервал ε относительно оценки математического ожидания , внутри которого с вероятностью 0.8 расположено истинное значение математического ожидания m:

Из курса теории вероятностей известно, что для этого необходимо вычислить обратную функцию распределения исследуемой случайной величины. Наше среднее является суммой независимых одинаково распределенных случайных величин Х_i (i=1..20) и, согласно центральной предельной теореме, при достаточно большом числе опытов ее закон распределения близок к нормальному. На практике, даже при относительно небольшом числе слагаемых (порядка 10 – 20) закон распределения суммы можно считать нормальным. Поэтому будем считать, что m – нормально распределенная случайная величина. В этом случае необходимо использовать обратную функцию Лапласа Φ^-1.

В Маткаде имеется встроенная функция qnorm(p,m,σ), являющаяся обратной функцией нормального распределения. Здесь р – заданная вероятность, m- математическое ожидание, а σ –среднеквадратическое отклонение нормально распределенной случайной величины. Функция qnorm возвращает отрезок -∞ - х, оси абсцисс, на котором находится случайная величина х с заданной вероятностью р.

Нас интересует отрезок , внутри которого с вероятностью 0,8 должно находиться математическое ожидание m.

Для лучшего понимания, что нам необходимо сделать, рассмотрим рис.2

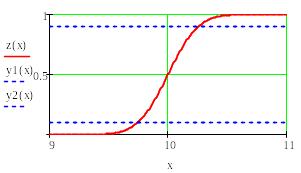
Рис.2. Доверительный интервал для нормальной функции распределения.

На этом рисунке кривая – функция распределения нормально распределенной случайной величины с математическим ожиданием m=10 и среднеквадратическим отклонением σ=0,2. Функция распределения F(x) показывает вероятность попадания случайной величины х на отрезок оси абсцисс (-∞, х). Из рисунка видно, что эта вероятность для х= m равна 0.5. Нам нужно найти такие отрезки на оси х, границы которых соответствуют вероятностям 0,5+0,4 и 0,5-0,4. Их длину мы обозначим через ε1 и ε2 .Эти вероятности обозначены на рисунке пунктирными горизонтальными линиями. Нахождение отрезков и границ доверительной области в Маткаде показано на рис.3. В первой строке производится вычисление верхнего интервала и верхней границы доверительной области, во второй – нижнего интервала и нижней границы области.

Задача решена.

.

Рис.3. Вычисление отрезков ε1 и ε2 и границ доверительной области .

Проверка статистических гипотез в пакете Маткад.

Произведено 500 наблюдений. Результаты наблюдений сведены в статистический ряд:

Интервалы Наблюдений	-4-;3	-3;-2	-2;-1	-1;0	0;1	1;2	2;3	3;4
Число наблюдений в данном интервале	6	25	72	133	120	88	46	10
Частота m/n	0.012	0.05	0.144	0.266	0.240	0.176	0.092	0.02

Задано среднее этих наблюдений m=0.2 и среднеквадратическое отклонение s=1.5.

Требуется построить гистограмму этого ряда, выбрать в качестве теоретического нормальное распределение и проверить его согласованность со статистическим распределением. В качестве параметров теоретического нормального распределения выбрать статистическое среднее и статистическое среднеквадратическое отклонение.

Решение в Маткаде.

Гистограмма для этой задачи была построена в лабораторной работе №6 модуля 1. Поэтому здесь только приводятся ее график и векторы интервалов и частот.

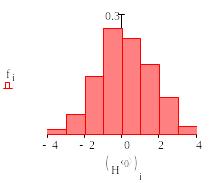
Рис.4. График гистограммы и векторы интервалов и частоты

После построения гистограммы с помощью встроенной функции dnorm(x, 0.2,1.35) строим график нормального закона распределения и вычисляем вероятности попадания случайной величины в каждый интервал. Как известно, эта вероятность равна интегралу от кривой распределения в пределах границ участка.

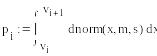
Рис.5.График гистограммы и теоретического нормального распределения

Далее (см. рис.6), вычисляем значение χ² (мы обозначили его через U), оно равно 3.899, и вызываем встроенную функцию Маткада pchisq. Если ввести в нее вычисленное значение U и число «степеней свободы», то в ответ получим вероятность противоречивости гипотезы о нормальном распределении наших наблюдений. В нашем случае число степеней свободы равно пяти, так как у нас восемь интервалов, и мы накладываем три условия:

1. сумма теоретических вероятностей равна 1,

2. задаемся математическим ожиданием теоретического распределения,

3. задаемся среднеквадратическим отклонением теоретического распределения.

К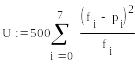 ак известно, число степеней свободы равно разности числа интервалов и числа условий. В результате мы получили вероятность р=0.436. Это вероятность несоответствия наблюдений нашей гипотезе.

Рис.6. Вычисление вероятности несоответствия наблюдений гипотезе о нормальности

Следовательно, вероятность соответствия рсоотв. = 1- pchisq = 0.564

Это достаточно хорошая вероятность того, что наши наблюдения распределены нормально.

РЕКОМЕДУЕМЫЕ ИСТОЧНИКИ

1.Очков В.Ф. Mathcad 14 для студентов, инженеров и конструкторов БХВ- Петербург 2007

2.Очков В.Ф. Мультимедийный обучающий курс по Mathcad 13. Курс создан на фирме Мультимедиа Технологии – (495) 673-76-92, www.mmt-dl.ru

3. Интернет- форум exponenta.ru//Mathcad

4. Краснов А.Е. и др. Информационные технологии пищевых производств в условиях неопределенности. М.,2001

5. Краснов А.Е. и др. Основы математического моделирования рецептурных смесей пищевой биотехнологии. М., Пищепромиздат ,2006

6.Грачев.Ю.П. и др. Моделирование и оптимизация тепло- и массообменов пищевых производств .М., Легкая и пищевая промышленность,1984

Яньков Владимир Юрьевич